斐波那契堆(Fibonacci heap)是一种可合并堆，可用于实现合并优先队列。它比二项堆具有更好的平摊分析性能，它的合并操作的时间复杂度是O(1)。
与二项堆一样，它也是由一组堆最小有序树组成，并且是一种可合并堆。
与二项堆不同的是，斐波那契堆中的树不一定是二项树；而且二项堆中的树是有序排列的，但是斐波那契堆中的树都是有根而无序的。

斐波那契堆的基本操作

1. 基本定义

public class FibHeap {

    private int keyNum;         // 堆中节点的总数
    private FibNode min;        // 最小节点(某个最小堆的根节点)

    private class FibNode {
        int key;            // 关键字(键值)
        int degree;         // 度数
        FibNode left;       // 左兄弟
        FibNode right;      // 右兄弟
        FibNode child;      // 第一个孩子节点
        FibNode parent;     // 父节点
        boolean marked;     // 是否被删除第一个孩子

        public FibNode(int key) {
            this.key    = key;
            this.degree = 0;
            this.marked = false;
            this.left   = this;
            this.right  = this;
            this.parent = null;
            this.child  = null;
        }
    }

    ...
}

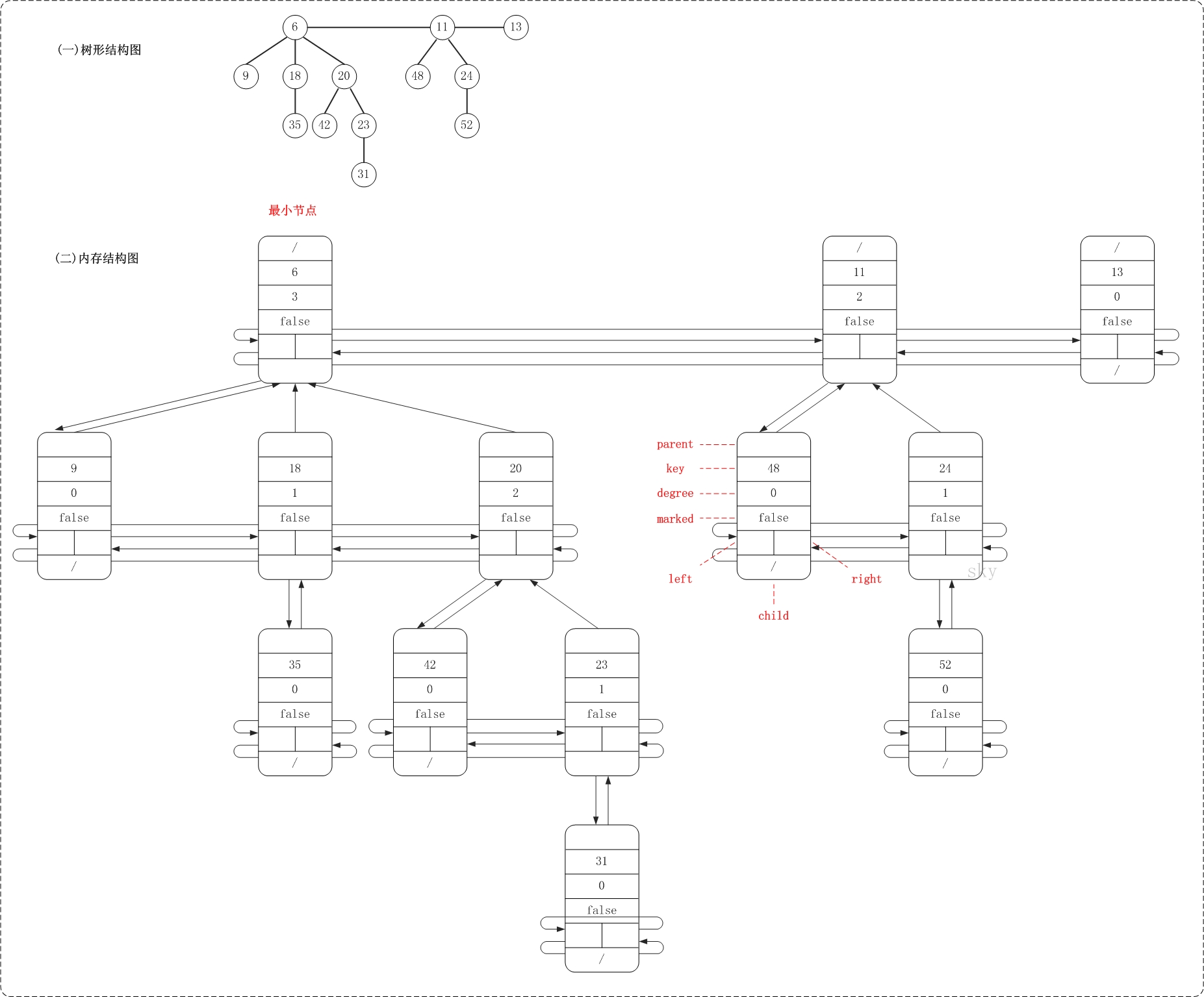
FibNode是斐波那契堆的节点类，它包含的信息较多。key是用于比较节点大小的，degree是记录节点的度，left和right分别是指向节点的左右兄弟，child是节点的第一个孩子，parent是节点的父节点，marked是记录该节点是否被删除第1个孩子(marked在删除节点时有用)。
FibHeap是斐波那契堆对应的类。min是保存当前堆的最小节点，keyNum用于记录堆中节点的总数，maxDegree用于记录堆中最大度，而cons在删除节点时来暂时保存堆数据的临时空间。

上面是斐波那契堆的两种不同结构图的对比。从中可以看出，斐波那契堆是由一组最小堆组成，这些最小堆的根节点组成了双向链表(后文称为"根链表")；斐波那契堆中的最小节点就是"根链表中的最小节点"！

PS. 上面这幅图的结构和测试代码中的"基本信息"测试函数的结果是一致的；你可以通过测试程序来亲自验证！

2. 插入操作

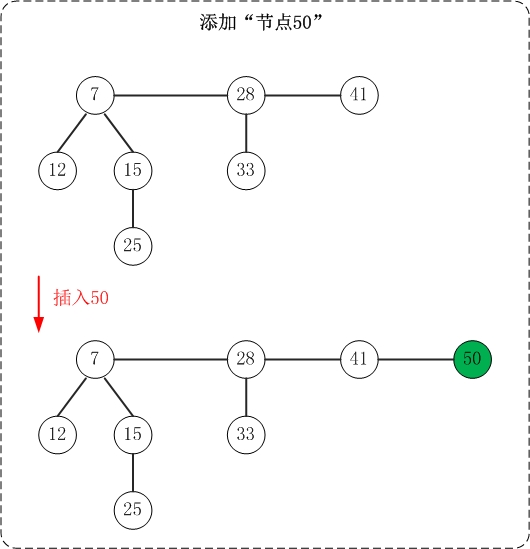
插入操作非常简单：插入一个节点到堆中，直接将该节点插入到"根链表的min节点"之前即可；若被插入节点比"min节点"小，则更新"min节点"为被插入节点。

上面是插入操作的示意图。

斐波那契堆的根链表是"双向链表"，这里将min节点看作双向联表的表头(后文也是如此)。在插入节点时，每次都是"将节点插入到min节点之前(即插入到双链表末尾)"。此外，对于根链表中最小堆都只有一个节点的情况，插入操作就很演化成双向链表的插入操作。

此外，插入操作示意图与测试程序中的"插入操作"相对应，感兴趣的可以亲自验证。

插入操作代码

/*
 * 将node堆结点加入root结点之前(循环链表中)
 *   a …… root
 *   a …… node …… root
*/
private void addNode(FibNode node, FibNode root) {
    node.left        = root.left;
    root.left.right  = node;
    node.right       = root;
    root.left        = node;
}
 
/*
 * 将节点node插入到斐波那契堆中
 */
private void insert(FibNode node) {
    if (keyNum == 0)
        min = node;
    else {
        addNode(node, min);
        if (node.key < min.key)
            min = node;
    }

    keyNum++;
}
 
/* 
 * 新建键值为key的节点，并将其插入到斐波那契堆中
 */
public void insert(int key) {
    FibNode node;

    node = new FibNode(key);
    if (node == null)
        return ;

    insert(node);
}

3. 合并操作

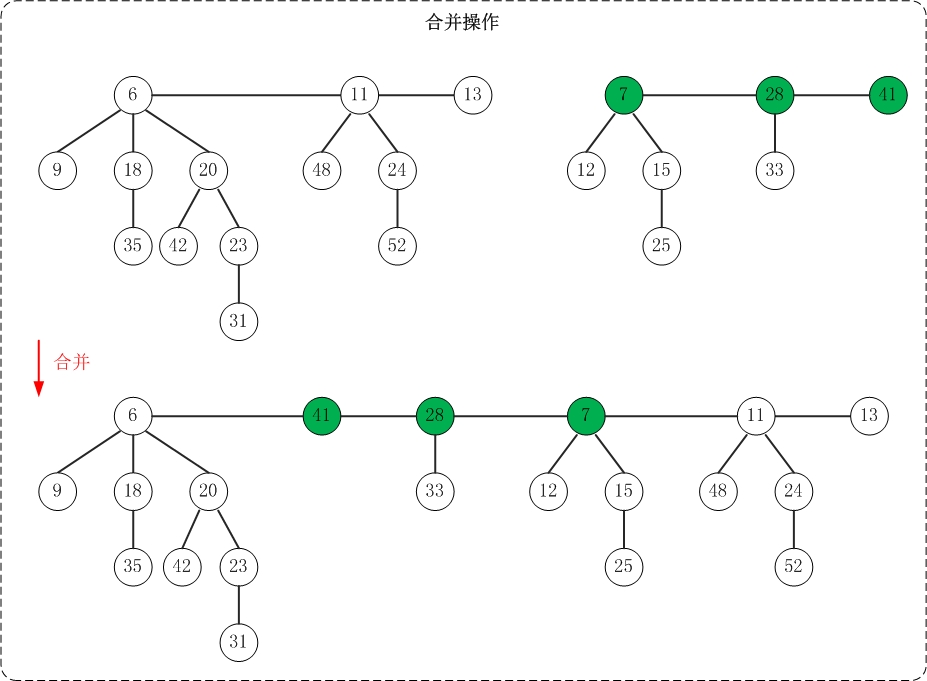
合并操作和插入操作的原理非常类似：将一个堆的根链表插入到另一个堆的根链表上即可。简单来说，就是将两个双链表拼接成一个双向链表。

上面是合并操作的示意图。该操作示意图与测试程序中的"合并操作"相对应！

合并操作代码

/*
* 将双向链表b链接到双向链表a的后面
*/
private void catList(FibNode a, FibNode b) {
    FibNode tmp;

    tmp           = a.right;
    a.right       = b.right;
    b.right.left  = a;
    b.right       = tmp;
    tmp.left      = b;
}

/*
 * 将other合并到当前堆中
 */
public void union(FibHeap other) {
    if (other==null)
        return ;

    if((this.min) == null) {                // this无"最小节点"
        this.min = other.min;
        this.keyNum = other.keyNum;
        other = null;
    } else if((other.min) == null) {        // this有"最小节点" && other无"最小节点"
        other = null;
    } else {                                // this有"最小节点" && other有"最小节点"
        // 将"other中根链表"添加到"this"中
    catList(this.min, other.min) ;

        if (this.min.key > other.min.key)
            this.min = other.min;
        this.keyNum += other.keyNum;
        other = null;;
    }
}

4. 取出最小节点

抽取最小结点的操作是斐波那契堆中较复杂的操作。
(1）将要抽取最小结点的子树都直接串联在根表中；
(2）合并所有degree相等的树，直到没有相等的degree的树。

上面是取出最小节点的示意图。图中应该写的非常明白了，若有疑问，看代码。

此外，该操作示意图与测试程序中的"删除最小节点"相对应！有兴趣的可以亲自验证。

取出最小节点代码

/*
 * 将node链接到root根结点
 */
private void link(FibNode node, FibNode root) {
    // 将node从双链表中移除
    removeNode(node);
    // 将node设为root的孩子
    if (root.child == null)
        root.child = node;
    else
        addNode(node, root.child);

    node.parent = root;
    root.degree++;
    node.marked = false;
}
 
/* 
 * 合并斐波那契堆的根链表中左右相同度数的树
 */
private void consolidate() {
// 计算log2(keyNum)，floor意味着向上取整！
// ex. log2(13) = 3，向上取整为4。
    int maxDegree = (int) Math.floor(Math.log(keyNum) / Math.log(2.0));
    int D = maxDegree + 1;
    FibNode[] cons = new FibNode[D+1];

    for (int i = 0; i < D; i++)
        cons[i] = null;
 
    // 合并相同度的根节点，使每个度数的树唯一
    while (min != null) {
        FibNode x = extractMin();            // 取出堆中的最小树(最小节点所在的树)
        int d = x.degree;                        // 获取最小树的度数
        // cons[d] != null，意味着有两棵树(x和y)的"度数"相同。
        while (cons[d] != null) {
            FibNode y = cons[d];                // y是"与x的度数相同的树" 
            if (x.key > y.key) {    // 保证x的键值比y小
                FibNode tmp = x;
                x = y;
                y = tmp;
            }

            link(y, x);    // 将y链接到x中
            cons[d] = null;
            d++;
        }
        cons[d] = x;
    }
    min = null;
 
    // 将cons中的结点重新加到根表中
    for (int i=0; i<D; i++) {

        if (cons[i] != null) {
            if (min == null)
                min = cons[i];
            else {
                addNode(cons[i], min);
                if ((cons[i]).key < min.key)
                    min = cons[i];
            }
        }
    }
}
 
/*
 * 移除最小节点
 */
public void removeMin() {
    if (min==null)
        return ;

    FibNode m = min;
    // 将min每一个儿子(儿子和儿子的兄弟)都添加到"斐波那契堆的根链表"中
    while (m.child != null) {
        FibNode child = m.child;

        removeNode(child);
        if (child.right == child)
            m.child = null;
        else
            m.child = child.right;

        addNode(child, min);
        child.parent = null;
    }

    // 将m从根链表中移除
    removeNode(m);
    // 若m是堆中唯一节点，则设置堆的最小节点为null；
    // 否则，设置堆的最小节点为一个非空节点(m.right)，然后再进行调节。
    if (m.right == m)
        min = null;
    else {
        min = m.right;
        consolidate();
    }
    keyNum--;

    m = null;
}

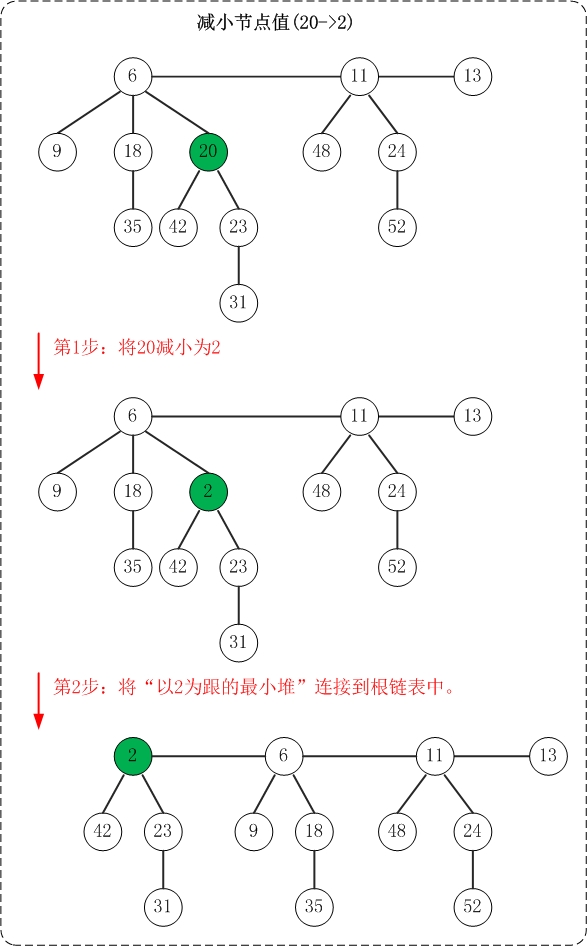
5. 减小节点值

减少斐波那契堆中的节点的键值，这个操作的难点是：如果减少节点后破坏了"最小堆"性质，如何去维护呢？下面对一般性情况进行分析。
(1) 首先，将"被减小节点"从"它所在的最小堆"剥离出来；然后将"该节点"关联到"根链表"中。倘若被减小的节点不是单独一个节点，而是包含子树的树根。则是将以"被减小节点"为根的子树从"最小堆"中剥离出来，然后将该树关联到根链表中。
(2) 接着，对"被减少节点"的原父节点进行"级联剪切"。所谓"级联剪切"，就是在被减小节点破坏了最小堆性质，并被切下来之后；再从"它的父节点"进行递归级联剪切操作。
而级联操作的具体动作则是：若父节点(被减小节点的父节点)的marked标记为false，则将其设为true，然后退出。
否则，将父节点从最小堆中切下来(方式和"切被减小节点的方式"一样)；然后递归对祖父节点进行"级联剪切"。
marked标记的作用就是用来标记"该节点的子节点是否有被删除过"，它的作用是来实现级联剪切。而级联剪切的真正目的是为了防止"最小堆"由二叉树演化成链表。
(3) 最后，别忘了对根链表的最小节点进行更新。

上面是减小节点值的示意图。该操作示意图与测试程序中的"减小节点"相对应！

减小节点值的代码

/* 
 * 修改度数
 */
private void renewDegree(FibNode parent, int degree) {
    parent.degree -= degree;
    if (parent. parent != null)
        renewDegree(parent.parent, degree);
}
 
/* 
 * 将node从父节点parent的子链接中剥离出来，
 * 并使node成为"堆的根链表"中的一员。
 */
private void cut(FibNode node, FibNode parent) {
    removeNode(node);
    renewDegree(parent, node.degree);
    // node没有兄弟
    if (node == node.right) 
        parent.child = null;
    else 
        parent.child = node.right;

    node.parent = null;
    node.left = node.right = node;
    node.marked = false;
    // 将"node所在树"添加到"根链表"中
    addNode(node, min);
}

/* 
 * 对节点node进行"级联剪切"
 *
 * 级联剪切：如果减小后的结点破坏了最小堆性质，
 *     则把它切下来(即从所在双向链表中删除，并将
 *     其插入到由最小树根节点形成的双向链表中)，
 *     然后再从"被切节点的父节点"到所在树根节点递归执行级联剪枝
 */
private void cascadingCut(FibNode node) {
    FibNode parent = node.parent;

    if (parent != null) {
        if (node.marked == false) 
            node.marked = true;
        else {
            cut(node, parent);
            cascadingCut(parent);
        }
    }
}

/* 
 * 将斐波那契堆中节点node的值减少为key
 */
private void decrease(FibNode node, int key) {
    if (min==null ||node==null) 
        return ;

    if (key > node.key) {
    System.out.printf("decrease failed: the new key(%d) is no smaller than current key(%d)\n", key, node.key);
        return ;
    }

    FibNode parent = node.parent;
    node.key = key;
    if (parent!=null && (node.key < parent.key)) {
        // 将node从父节点parent中剥离出来，并将node添加到根链表中
        cut(node, parent);
        cascadingCut(parent);
    }

    // 更新最小节点
    if (node.key < min.key)
        min = node;
}

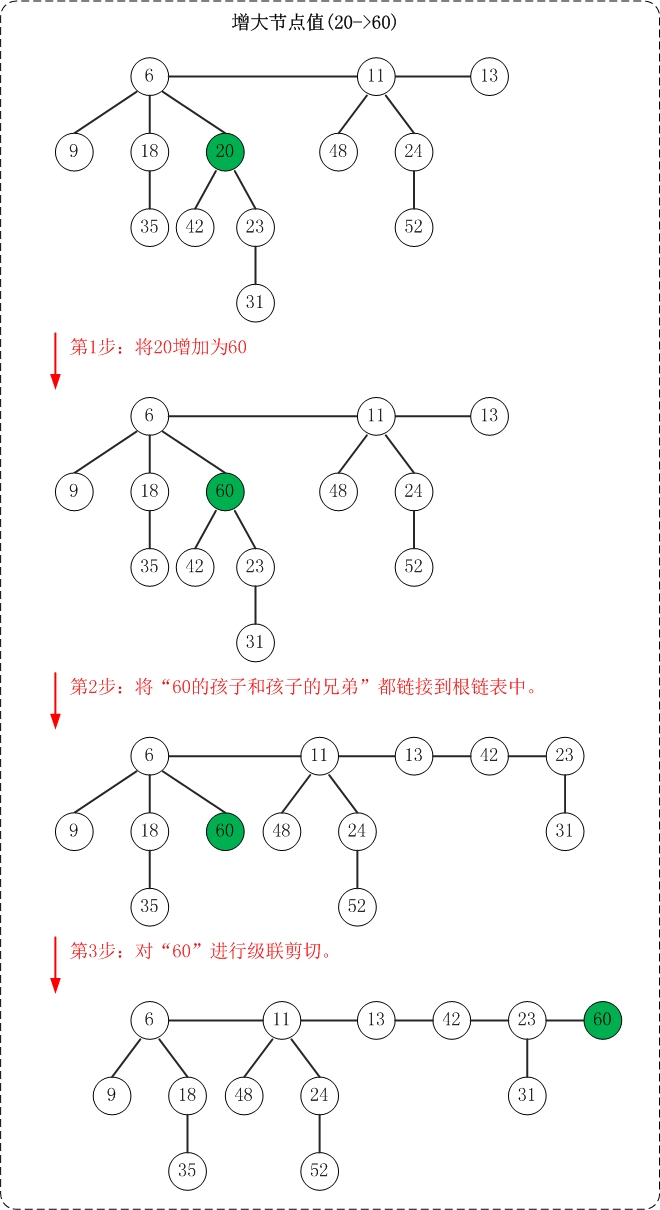
6. 增加节点值

增加节点值和减少节点值类似，这个操作的难点也是如何维护"最小堆"性质。思路如下：
(1) 将"被增加节点"的"左孩子和左孩子的所有兄弟"都链接到根链表中。
(2) 接下来，把"被增加节点"添加到根链表；但是别忘了对其进行级联剪切。

上面是增加节点值的示意图。该操作示意图与测试程序中的"增大节点"相对应！

增加节点值的代码

/* 
 * 将斐波那契堆中节点node的值增加为key
 */
private void increase(FibNode node, int key) {
    if (min==null ||node==null) 
        return ;

    if ( key <= node.key) {
    System.out.printf("increase failed: the new key(%d) is no greater than current key(%d)\n", key, node.key);
        return ;
    }

    // 将node每一个儿子(不包括孙子,重孙,...)都添加到"斐波那契堆的根链表"中
    while (node.child != null) {
        FibNode child = node.child;
        removeNode(child);               // 将child从node的子链表中删除
        if (child.right == child)
            node.child = null;
        else
            node.child = child.right;

        addNode(child, min);       // 将child添加到根链表中
        child.parent = null;
    }
    node.degree = 0;
    node.key = key;

    // 如果node不在根链表中，
    //     则将node从父节点parent的子链接中剥离出来，
    //     并使node成为"堆的根链表"中的一员，
    //     然后进行"级联剪切"
    // 否则，则判断是否需要更新堆的最小节点
    FibNode parent = node.parent;
    if(parent != null) {
        cut(node, parent);
        cascadingCut(parent);
    } else if(min == node) {
        FibNode right = node.right;
        while(right != node) {
            if(node.key > right.key)
                min = right;
            right = right.right;
        }
    }
}

7. 删除节点

删除节点，本文采用了操作是："取出最小节点"和"减小节点值"的组合。
(1) 先将被删除节点的键值减少。减少后的值要比"原最小节点的值"即可。
(2) 接着，取出最小节点即可。

删除节点值的代码

/*
 * 删除结点node
 */
private void remove(FibNode node) {
    int m = min.key;
    decrease(node, m-1);
    removeMin();
}

注意：关于斐波那契堆的"更新"、"打印"、"销毁"等接口就不再单独介绍了。后文的源码中有给出它们的实现代码，Please RTFSC(Read The Fucking Source Code)！

斐波那契堆的Java实现(完整源码)

斐波那契堆的实现文件(FibHeap.java)

  1 /**
  2  * Java 语言: 斐波那契堆
  3  *
  4  * @author skywang
  5  * @date 2014/04/07
  6  */
  7 
  8 public class FibHeap {
  9 
 10     private int keyNum;         // 堆中节点的总数
 11     private FibNode min;        // 最小节点(某个最小堆的根节点)
 12 
 13     private class FibNode {
 14         int key;            // 关键字(键值)
 15         int degree;            // 度数
 16         FibNode left;        // 左兄弟
 17         FibNode right;        // 右兄弟
 18         FibNode child;        // 第一个孩子节点
 19         FibNode parent;        // 父节点
 20         boolean marked;     // 是否被删除第一个孩子
 21 
 22         public FibNode(int key) {
 23             this.key    = key;
 24             this.degree = 0;
 25             this.marked = false;
 26             this.left   = this;
 27             this.right  = this;
 28             this.parent = null;
 29             this.child  = null;
 30         }
 31     }
 32 
 33     public FibHeap() {
 34         this.keyNum = 0;
 35         this.min = null;
 36     }
 37 
 38     /* 
 39      * 将node从双链表移除
 40      */
 41     private void removeNode(FibNode node) {
 42         node.left.right = node.right;
 43         node.right.left = node.left;
 44     }
 45      
 46     /*
 47      * 将node堆结点加入root结点之前(循环链表中)
 48      *   a …… root
 49      *   a …… node …… root
 50     */
 51     private void addNode(FibNode node, FibNode root) {
 52         node.left        = root.left;
 53         root.left.right  = node;
 54         node.right       = root;
 55         root.left        = node;
 56     }
 57      
 58     /*
 59      * 将节点node插入到斐波那契堆中
 60      */
 61     private void insert(FibNode node) {
 62         if (keyNum == 0)
 63             min = node;
 64         else {
 65             addNode(node, min);
 66             if (node.key < min.key)
 67                 min = node;
 68         }
 69 
 70         keyNum++;
 71     }
 72      
 73     /* 
 74      * 新建键值为key的节点，并将其插入到斐波那契堆中
 75      */
 76     public void insert(int key) {
 77         FibNode node;
 78 
 79         node = new FibNode(key);
 80         if (node == null)
 81             return ;
 82 
 83         insert(node);
 84     }
 85      
 86     /*
 87      * 将双向链表b链接到双向链表a的后面
 88      */
 89     private void catList(FibNode a, FibNode b) {
 90         FibNode tmp;
 91 
 92         tmp           = a.right;
 93         a.right       = b.right;
 94         b.right.left  = a;
 95         b.right       = tmp;
 96         tmp.left      = b;
 97     }
 98 
 99     /*
100      * 将other合并到当前堆中
101      */
102     public void union(FibHeap other) {
103         if (other==null)
104             return ;
105 
106         if((this.min) == null) {                // this无"最小节点"
107             this.min = other.min;
108             this.keyNum = other.keyNum;
109             other = null;
110         } else if((other.min) == null) {        // this有"最小节点" && other无"最小节点"
111             other = null;
112         } else {                                // this有"最小节点" && other有"最小节点"
113             // 将"other中根链表"添加到"this"中
114             catList(this.min, other.min) ;
115 
116             if (this.min.key > other.min.key)
117                 this.min = other.min;
118             this.keyNum += other.keyNum;
119             other = null;;
120         }
121     }
122 
123     /*
124      * 将"堆的最小结点"从根链表中移除，
125      * 这意味着"将最小节点所属的树"从堆中移除!
126      */
127     private FibNode extractMin() {
128         FibNode p = min;
129 
130         if (p == p.right)
131             min = null;
132         else {
133             removeNode(p);
134             min = p.right;
135         }
136         p.left = p.right = p;
137 
138         return p;
139     }
140      
141     /*
142      * 将node链接到root根结点
143      */
144     private void link(FibNode node, FibNode root) {
145         // 将node从双链表中移除
146         removeNode(node);
147         // 将node设为root的孩子
148         if (root.child == null)
149             root.child = node;
150         else
151             addNode(node, root.child);
152 
153         node.parent = root;
154         root.degree++;
155         node.marked = false;
156     }
157      
158     /* 
159      * 合并斐波那契堆的根链表中左右相同度数的树
160      */
161     private void consolidate() {
162         // 计算log2(keyNum)，floor意味着向上取整！
163         // ex. log2(13) = 3，向上取整为4。
164         int maxDegree = (int) Math.floor(Math.log(keyNum) / Math.log(2.0));
165         int D = maxDegree + 1;
166         FibNode[] cons = new FibNode[D+1];
167 
168         for (int i = 0; i < D; i++)
169             cons[i] = null;
170      
171         // 合并相同度的根节点，使每个度数的树唯一
172         while (min != null) {
173             FibNode x = extractMin();            // 取出堆中的最小树(最小节点所在的树)
174             int d = x.degree;                        // 获取最小树的度数
175             // cons[d] != null，意味着有两棵树(x和y)的"度数"相同。
176             while (cons[d] != null) {
177                 FibNode y = cons[d];                // y是"与x的度数相同的树" 
178                 if (x.key > y.key) {    // 保证x的键值比y小
179                     FibNode tmp = x;
180                     x = y;
181                     y = tmp;
182                 }
183 
184                 link(y, x);    // 将y链接到x中
185                 cons[d] = null;
186                 d++;
187             }
188             cons[d] = x;
189         }
190         min = null;
191      
192         // 将cons中的结点重新加到根表中
193         for (int i=0; i<D; i++) {
194 
195             if (cons[i] != null) {
196                 if (min == null)
197                     min = cons[i];
198                 else {
199                     addNode(cons[i], min);
200                     if ((cons[i]).key < min.key)
201                         min = cons[i];
202                 }
203             }
204         }
205     }
206      
207     /*
208      * 移除最小节点
209      */
210     public void removeMin() {
211         if (min==null)
212             return ;
213 
214         FibNode m = min;
215         // 将min每一个儿子(儿子和儿子的兄弟)都添加到"斐波那契堆的根链表"中
216         while (m.child != null) {
217             FibNode child = m.child;
218 
219             removeNode(child);
220             if (child.right == child)
221                 m.child = null;
222             else
223                 m.child = child.right;
224 
225             addNode(child, min);
226             child.parent = null;
227         }
228 
229         // 将m从根链表中移除
230         removeNode(m);
231         // 若m是堆中唯一节点，则设置堆的最小节点为null；
232         // 否则，设置堆的最小节点为一个非空节点(m.right)，然后再进行调节。
233         if (m.right == m)
234             min = null;
235         else {
236             min = m.right;
237             consolidate();
238         }
239         keyNum--;
240 
241         m = null;
242     }
243 
244     /*
245      * 获取斐波那契堆中最小键值；失败返回-1
246      */
247     public int minimum() {
248         if (min==null)
249             return -1;
250 
251         return min.key;
252     }
253       
254     /* 
255      * 修改度数
256      */
257     private void renewDegree(FibNode parent, int degree) {
258         parent.degree -= degree;
259         if (parent. parent != null)
260             renewDegree(parent.parent, degree);
261     }
262      
263     /* 
264      * 将node从父节点parent的子链接中剥离出来，
265      * 并使node成为"堆的根链表"中的一员。
266      */
267     private void cut(FibNode node, FibNode parent) {
268         removeNode(node);
269         renewDegree(parent, node.degree);
270         // node没有兄弟
271         if (node == node.right) 
272             parent.child = null;
273         else 
274             parent.child = node.right;
275 
276         node.parent = null;
277         node.left = node.right = node;
278         node.marked = false;
279         // 将"node所在树"添加到"根链表"中
280         addNode(node, min);
281     }
282 
283     /* 
284      * 对节点node进行"级联剪切"
285      *
286      * 级联剪切：如果减小后的结点破坏了最小堆性质，
287      *     则把它切下来(即从所在双向链表中删除，并将
288      *     其插入到由最小树根节点形成的双向链表中)，
289      *     然后再从"被切节点的父节点"到所在树根节点递归执行级联剪枝
290      */
291     private void cascadingCut(FibNode node) {
292         FibNode parent = node.parent;
293 
294         if (parent != null) {
295             if (node.marked == false) 
296                 node.marked = true;
297             else {
298                 cut(node, parent);
299                 cascadingCut(parent);
300             }
301         }
302     }
303 
304     /* 
305      * 将斐波那契堆中节点node的值减少为key
306      */
307     private void decrease(FibNode node, int key) {
308         if (min==null ||node==null) 
309             return ;
310 
311         if (key > node.key) {
312             System.out.printf("decrease failed: the new key(%d) is no smaller than current key(%d)\n", key, node.key);
313             return ;
314         }
315 
316         FibNode parent = node.parent;
317         node.key = key;
318         if (parent!=null && (node.key < parent.key)) {
319             // 将node从父节点parent中剥离出来，并将node添加到根链表中
320             cut(node, parent);
321             cascadingCut(parent);
322         }
323 
324         // 更新最小节点
325         if (node.key < min.key)
326             min = node;
327     }
328 
329     /* 
330      * 将斐波那契堆中节点node的值增加为key
331      */
332     private void increase(FibNode node, int key) {
333         if (min==null ||node==null) 
334             return ;
335 
336         if ( key <= node.key) {
337             System.out.printf("increase failed: the new key(%d) is no greater than current key(%d)\n", key, node.key);
338             return ;
339         }
340 
341         // 将node每一个儿子(不包括孙子,重孙,...)都添加到"斐波那契堆的根链表"中
342         while (node.child != null) {
343             FibNode child = node.child;
344             removeNode(child);               // 将child从node的子链表中删除
345             if (child.right == child)
346                 node.child = null;
347             else
348                 node.child = child.right;
349 
350             addNode(child, min);       // 将child添加到根链表中
351             child.parent = null;
352         }
353         node.degree = 0;
354         node.key = key;
355 
356         // 如果node不在根链表中，
357         //     则将node从父节点parent的子链接中剥离出来，
358         //     并使node成为"堆的根链表"中的一员，
359         //     然后进行"级联剪切"
360         // 否则，则判断是否需要更新堆的最小节点
361         FibNode parent = node.parent;
362         if(parent != null) {
363             cut(node, parent);
364             cascadingCut(parent);
365         } else if(min == node) {
366             FibNode right = node.right;
367             while(right != node) {
368                 if(node.key > right.key)
369                     min = right;
370                 right = right.right;
371             }
372         }
373     }
374 
375     /* 
376      * 更新斐波那契堆的节点node的键值为key
377      */
378     private void update(FibNode node, int key) {
379         if(key < node.key)
380             decrease(node, key);
381         else if(key > node.key)
382             increase(node, key);
383         else
384             System.out.printf("No need to update!!!\n");
385     }
386       
387     public void update(int oldkey, int newkey) {
388         FibNode node;
389 
390         node = search(oldkey);
391         if (node!=null)
392             update(node, newkey);
393     }
394 
395     /*
396      * 在最小堆root中查找键值为key的节点
397      */
398     private FibNode search(FibNode root, int key) {
399         FibNode t = root;    // 临时节点
400         FibNode p = null;    // 要查找的节点
401 
402         if (root==null)
403             return root;
404 
405         do {
406             if (t.key == key) {
407                 p = t;
408                 break;
409             } else {
410                 if ((p = search(t.child, key)) != null) 
411                     break;
412             }
413             t = t.right;
414         } while (t != root);
415 
416         return p;
417     }
418      
419     /*
420      * 在斐波那契堆中查找键值为key的节点
421      */
422     private FibNode search(int key) {
423         if (min==null)
424             return null;
425 
426         return search(min, key);
427     }
428 
429     /*
430      * 在斐波那契堆中是否存在键值为key的节点。
431      * 存在返回true，否则返回false。
432      */
433     public boolean contains(int key) {
434         return search(key)!=null ? true: false;
435     }
436 
437     /*
438      * 删除结点node
439      */
440     private void remove(FibNode node) {
441         int m = min.key;
442         decrease(node, m-1);
443         removeMin();
444     }
445 
446     public void remove(int key) {
447         if (min==null)
448             return ;
449 
450         FibNode node = search(key);
451         if (node==null)
452             return ;
453 
454         remove(node);
455     }
456      
457     /* 
458      * 销毁斐波那契堆
459      */
460     private void destroyNode(FibNode node) {
461         if(node == null)
462             return;
463 
464         FibNode start = node;
465         do {
466             destroyNode(node.child);
467             // 销毁node，并将node指向下一个
468             node = node.right;
469             node.left = null;
470         } while(node != start);
471     }
472      
473     public void destroy() {
474         destroyNode(min);
475     }
476 
477     /*
478      * 打印"斐波那契堆"
479      *
480      * 参数说明：
481      *     node       -- 当前节点
482      *     prev       -- 当前节点的前一个节点(父节点or兄弟节点)
483      *     direction  --  1，表示当前节点是一个左孩子;
484      *                    2，表示当前节点是一个兄弟节点。
485      */
486     private void print(FibNode node, FibNode prev, int direction) {
487         FibNode start=node;
488 
489         if (node==null)
490             return ;
491         do {
492             if (direction == 1)
493                 System.out.printf("%8d(%d) is %2d's child\n", node.key, node.degree, prev.key);
494             else
495                 System.out.printf("%8d(%d) is %2d's next\n", node.key, node.degree, prev.key);
496 
497             if (node.child != null)
498                 print(node.child, node, 1);
499 
500             // 兄弟节点
501             prev = node;
502             node = node.right;
503             direction = 2;
504         } while(node != start);
505     }
506 
507     public void print() {
508         if (min==null)
509             return ;
510 
511         int i=0;
512         FibNode p = min;
513         System.out.printf("== 斐波那契堆的详细信息: ==\n");
514         do {
515             i++;
516             System.out.printf("%2d. %4d(%d) is root\n", i, p.key, p.degree);
517 
518             print(p.child, p, 1);
519             p = p.right;
520         } while (p != min);
521         System.out.printf("\n");
522     }
523 }

View Code

斐波那契堆的测试程序(Main.java)

  1 /**
  2  * Java 语言: 斐波那契堆
  3  *
  4  * @author skywang
  5  * @date 2014/04/07
  6  */
  7 
  8 public class Main {
  9 
 10     private static final boolean DEBUG = false;
 11 
 12     // 共8个
 13     private static int a[] = {12,  7, 25, 15, 28, 33, 41, 1};
 14     // 共14个
 15     private static int b[] = {18, 35, 20, 42,  9, 
 16                                  31, 23,  6, 48, 11,
 17                               24, 52, 13,  2 };
 18 
 19     // 验证"基本信息(斐波那契堆的结构)"
 20     public static void testBasic() {
 21         FibHeap hb=new FibHeap();
 22 
 23         // 斐波那契堆hb
 24         System.out.printf("== 斐波那契堆(hb)中依次添加: ");
 25         for(int i=0; i<b.length; i++) {
 26             System.out.printf("%d ", b[i]);
 27             hb.insert(b[i]);
 28         }
 29         System.out.printf("\n");
 30         System.out.printf("== 斐波那契堆(hb)删除最小节点\n");
 31         hb.removeMin();
 32         hb.print(); // 打印斐波那契堆hb
 33     }
 34 
 35     // 验证"插入操作"
 36     public static void testInsert() {
 37         FibHeap ha=new FibHeap();
 38 
 39         // 斐波那契堆ha
 40         System.out.printf("== 斐波那契堆(ha)中依次添加: ");
 41         for(int i=0; i<a.length; i++) {
 42             System.out.printf("%d ", a[i]);
 43             ha.insert(a[i]);
 44         }
 45         System.out.printf("\n");
 46         System.out.printf("== 斐波那契堆(ha)删除最小节点\n");
 47         ha.removeMin();
 48         ha.print(); // 打印斐波那契堆ha
 49 
 50         System.out.printf("== 插入50\n");
 51         ha.insert(50);
 52         ha.print();
 53     }
 54 
 55     // 验证"合并操作"
 56     public static void testUnion() {
 57         FibHeap ha=new FibHeap();
 58         FibHeap hb=new FibHeap();
 59 
 60         // 斐波那契堆ha
 61         System.out.printf("== 斐波那契堆(ha)中依次添加: ");
 62         for(int i=0; i<a.length; i++) {
 63             System.out.printf("%d ", a[i]);
 64             ha.insert(a[i]);
 65         }
 66         System.out.printf("\n");
 67         System.out.printf("== 斐波那契堆(ha)删除最小节点\n");
 68         ha.removeMin();
 69         ha.print(); // 打印斐波那契堆ha
 70 
 71         // 斐波那契堆hb
 72         System.out.printf("== 斐波那契堆(hb)中依次添加: ");
 73         for(int i=0; i<b.length; i++) {
 74             System.out.printf("%d ", b[i]);
 75             hb.insert(b[i]);
 76         }
 77         System.out.printf("\n");
 78         System.out.printf("== 斐波那契堆(hb)删除最小节点\n");
 79         hb.removeMin();
 80         hb.print(); // 打印斐波那契堆hb
 81 
 82         // 将"斐波那契堆hb"合并到"斐波那契堆ha"中。
 83         System.out.printf("== 合并ha和hb\n");
 84         ha.union(hb);
 85         ha.print();
 86     }
 87 
 88     // 验证"删除最小节点"
 89     public static void testRemoveMin() {
 90         FibHeap ha=new FibHeap();
 91         FibHeap hb=new FibHeap();
 92 
 93         // 斐波那契堆ha
 94         System.out.printf("== 斐波那契堆(ha)中依次添加: ");
 95         for(int i=0; i<a.length; i++) {
 96             System.out.printf("%d ", a[i]);
 97             ha.insert(a[i]);
 98         }
 99         System.out.printf("\n");
100         System.out.printf("== 斐波那契堆(ha)删除最小节点\n");
101         ha.removeMin();
102         //ha.print(); // 打印斐波那契堆ha
103 
104         // 斐波那契堆hb
105         System.out.printf("== 斐波那契堆(hb)中依次添加: ");
106         for(int i=0; i<b.length; i++) {
107             System.out.printf("%d ", b[i]);
108             hb.insert(b[i]);
109         }
110         System.out.printf("\n");
111         System.out.printf("== 斐波那契堆(hb)删除最小节点\n");
112         hb.removeMin();
113         //hb.print(); // 打印斐波那契堆hb
114 
115         // 将"斐波那契堆hb"合并到"斐波那契堆ha"中。
116         System.out.printf("== 合并ha和hb\n");
117         ha.union(hb);
118         ha.print();
119 
120         System.out.printf("== 删除最小节点\n");
121         ha.removeMin();
122         ha.print();
123     }
124 
125     // 验证"减小节点"
126     public static void testDecrease() {
127         FibHeap hb=new FibHeap();
128 
129         // 斐波那契堆hb
130         System.out.printf("== 斐波那契堆(hb)中依次添加: ");
131         for(int i=0; i<b.length; i++) {
132             System.out.printf("%d ", b[i]);
133             hb.insert(b[i]);
134         }
135         System.out.printf("\n");
136         System.out.printf("== 斐波那契堆(hb)删除最小节点\n");
137         hb.removeMin();
138         hb.print(); // 打印斐波那契堆hb
139 
140         System.out.printf("== 将20减小为2\n");
141         hb.update(20, 2);
142         hb.print();
143     }
144 
145     // 验证"增大节点"
146     public static void testIncrease() {
147         FibHeap hb=new FibHeap();
148 
149         // 斐波那契堆hb
150         System.out.printf("== 斐波那契堆(hb)中依次添加: ");
151         for(int i=0; i<b.length; i++) {
152             System.out.printf("%d ", b[i]);
153             hb.insert(b[i]);
154         }
155         System.out.printf("\n");
156         System.out.printf("== 斐波那契堆(hb)删除最小节点\n");
157         hb.removeMin();
158         hb.print(); // 打印斐波那契堆hb
159 
160         System.out.printf("== 将20增加为60\n");
161         hb.update(20, 60);
162         hb.print();
163     }
164 
165     // 验证"删除节点"
166     public static void testDelete() {
167         FibHeap hb=new FibHeap();
168 
169         // 斐波那契堆hb
170         System.out.printf("== 斐波那契堆(hb)中依次添加: ");
171         for(int i=0; i<b.length; i++) {
172             System.out.printf("%d ", b[i]);
173             hb.insert(b[i]);
174         }
175         System.out.printf("\n");
176         System.out.printf("== 斐波那契堆(hb)删除最小节点\n");
177         hb.removeMin();
178         hb.print(); // 打印斐波那契堆hb
179 
180         System.out.printf("== 删除节点20\n");
181         hb.remove(20);
182         hb.print();
183     }
184 
185     public static void main(String[] args) {
186         // 验证"基本信息(斐波那契堆的结构)"
187         testBasic();
188         // 验证"插入操作"
189         //testInsert();
190         // 验证"合并操作"
191         //testUnion();
192         // 验证"删除最小节点"
193         //testRemoveMin();
194         // 验证"减小节点"
195         //testDecrease();
196         // 验证"增大节点"
197         //testIncrease();
198         // 验证"删除节点"
199         //testDelete();
200     }
201 }

View Code

斐波那契堆的Java测试程序

斐波那契堆的测试程序包括了"插入"、"合并"、"增大"、"减小"、"删除"、"基本信息"等几种功能的测试代码。默认是运行的"基本信息(验证斐波那契堆的结构)"测试代码，你可以根据自己的需要来对相应的功能进行验证！

下面是基本信息测试代码的运行结果：

== 斐波那契堆(hb)中依次添加: 18 35 20 42 9 31 23 6 48 11 24 52 13 2 
== 斐波那契堆(hb)删除最小节点
== 斐波那契堆的详细信息: ==
 1.    6(3) is root
       9(0) is  6's child
      18(1) is  9's next
      35(0) is 18's child
      20(2) is 18's next
      42(0) is 20's child
      23(1) is 42's next
      31(0) is 23's child
 2.   11(2) is root
      48(0) is 11's child
      24(1) is 48's next
      52(0) is 24's child
 3.   13(0) is root

posted on 2014-04-19 10:50 如果天空不死阅读(6784) 评论(3) 编辑收藏举报

刷新页面返回顶部

导航

概要

斐波那契堆的介绍

斐波那契堆的基本操作

斐波那契堆的Java实现(完整源码)

斐波那契堆的Java测试程序