概要
本章介绍伸展树。它和"二叉查找树"和"AVL树"一样,都是特殊的二叉树。在了解了"二叉查找树"和"AVL树"之后,学习伸展树是一件相当容易的事情。和以往一样,本文会先对伸展树的理论知识进行简单介绍,然后给出C语言的实现。后序再分别给出C++和Java版本的实现;这3种实现方式的原理都一样,选择其中之一进行了解即可。若文章有错误或不足的地方,希望您能不吝指出!
目录
1. 伸展树的介绍
2. 伸展树的C实现
3. 伸展树的C测试程序
转载请注明出处:http://www.cnblogs.com/skywang12345/p/3604238.html
更多内容: 数据结构与算法系列 目录
(01) 伸展树(一)之 图文解析 和 C语言的实现
(02) 伸展树(二)之 C++的实现
(03) 伸展树(三)之 Java的实现
伸展树的介绍
伸展树(Splay Tree)是一种二叉排序树,它能在O(log n)内完成插入、查找和删除操作。它由Daniel Sleator和Robert Tarjan创造。
(01) 伸展树属于二叉查找树,即它具有和二叉查找树一样的性质:假设x为树中的任意一个结点,x节点包含关键字key,节点x的key值记为key[x]。如果y是x的左子树中的一个结点,则key[y] <= key[x];如果y是x的右子树的一个结点,则key[y] >= key[x]。
(02) 除了拥有二叉查找树的性质之外,伸展树还具有的一个特点是:当某个节点被访问时,伸展树会通过旋转使该节点成为树根。这样做的好处是,下次要访问该节点时,能够迅速的访问到该节点。
假设想要对一个二叉查找树执行一系列的查找操作。为了使整个查找时间更小,被查频率高的那些条目就应当经常处于靠近树根的位置。于是想到设计一个简单方法,在每次查找之后对树进行重构,把被查找的条目搬移到离树根近一些的地方。伸展树应运而生,它是一种自调整形式的二叉查找树,它会沿着从某个节点到树根之间的路径,通过一系列的旋转把这个节点搬移到树根去。
相比于"二叉查找树"和"AVL树",学习伸展树时需要重点关注是"伸展树的旋转算法"。
伸展树的C实现
1. 节点定义
typedef int Type; typedef struct SplayTreeNode { Type key; // 关键字(键值) struct SplayTreeNode *left; // 左孩子 struct SplayTreeNode *right; // 右孩子 } Node, *SplayTree;
伸展树的节点包括的几个组成元素:
(01) key -- 是关键字,是用来对伸展树的节点进行排序的。
(02) left -- 是左孩子。
(03) right -- 是右孩子。
外部接口
// 前序遍历"伸展树" void preorder_splaytree(SplayTree tree); // 中序遍历"伸展树" void inorder_splaytree(SplayTree tree); // 后序遍历"伸展树" void postorder_splaytree(SplayTree tree); // (递归实现)查找"伸展树x"中键值为key的节点 Node* splaytree_search(SplayTree x, Type key); // (非递归实现)查找"伸展树x"中键值为key的节点 Node* iterative_splaytree_search(SplayTree x, Type key); // 查找最小结点:返回tree为根结点的伸展树的最小结点。 Node* splaytree_minimum(SplayTree tree); // 查找最大结点:返回tree为根结点的伸展树的最大结点。 Node* splaytree_maximum(SplayTree tree); // 旋转key对应的节点为根节点。 Node* splaytree_splay(SplayTree tree, Type key); // 将结点插入到伸展树中,并返回根节点 Node* insert_splaytree(SplayTree tree, Type key); // 删除结点(key为节点的值),并返回根节点 Node* delete_splaytree(SplayTree tree, Type key); // 销毁伸展树 void destroy_splaytree(SplayTree tree); // 打印伸展树 void print_splaytree(SplayTree tree, Type key, int direction);
2. 旋转
旋转的代码
/* * 旋转key对应的节点为根节点,并返回根节点。 * * 注意: * (a):伸展树中存在"键值为key的节点"。 * 将"键值为key的节点"旋转为根节点。 * (b):伸展树中不存在"键值为key的节点",并且key < tree->key。 * b-1 "键值为key的节点"的前驱节点存在的话,将"键值为key的节点"的前驱节点旋转为根节点。 * b-2 "键值为key的节点"的前驱节点存在的话,则意味着,key比树中任何键值都小,那么此时,将最小节点旋转为根节点。 * (c):伸展树中不存在"键值为key的节点",并且key > tree->key。 * c-1 "键值为key的节点"的后继节点存在的话,将"键值为key的节点"的后继节点旋转为根节点。 * c-2 "键值为key的节点"的后继节点不存在的话,则意味着,key比树中任何键值都大,那么此时,将最大节点旋转为根节点。 */ Node* splaytree_splay(SplayTree tree, Type key) { Node N, *l, *r, *c; if (tree == NULL) return tree; N.left = N.right = NULL; l = r = &N; for (;;) { if (key < tree->key) { if (tree->left == NULL) break; if (key < tree->left->key) { c = tree->left; /* 01, rotate right */ tree->left = c->right; c->right = tree; tree = c; if (tree->left == NULL) break; } r->left = tree; /* 02, link right */ r = tree; tree = tree->left; } else if (key > tree->key) { if (tree->right == NULL) break; if (key > tree->right->key) { c = tree->right; /* 03, rotate left */ tree->right = c->left; c->left = tree; tree = c; if (tree->right == NULL) break; } l->right = tree; /* 04, link left */ l = tree; tree = tree->right; } else { break; } } l->right = tree->left; /* 05, assemble */ r->left = tree->right; tree->left = N.right; tree->right = N.left; return tree; }
上面的代码的作用:将"键值为key的节点"旋转为根节点,并返回根节点。它的处理情况共包括:
(a):伸展树中存在"键值为key的节点"。
将"键值为key的节点"旋转为根节点。
(b):伸展树中不存在"键值为key的节点",并且key < tree->key。
b-1) "键值为key的节点"的前驱节点存在的话,将"键值为key的节点"的前驱节点旋转为根节点。
b-2) "键值为key的节点"的前驱节点存在的话,则意味着,key比树中任何键值都小,那么此时,将最小节点旋转为根节点。
(c):伸展树中不存在"键值为key的节点",并且key > tree->key。
c-1) "键值为key的节点"的后继节点存在的话,将"键值为key的节点"的后继节点旋转为根节点。
c-2) "键值为key的节点"的后继节点不存在的话,则意味着,key比树中任何键值都大,那么此时,将最大节点旋转为根节点。
下面列举个例子分别对a进行说明。
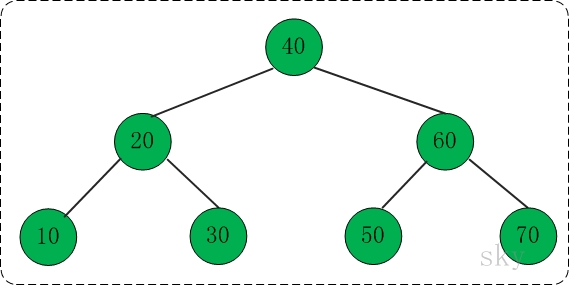
在下面的伸展树中查找10,共包括"右旋" --> "右链接" --> "组合"这3步。
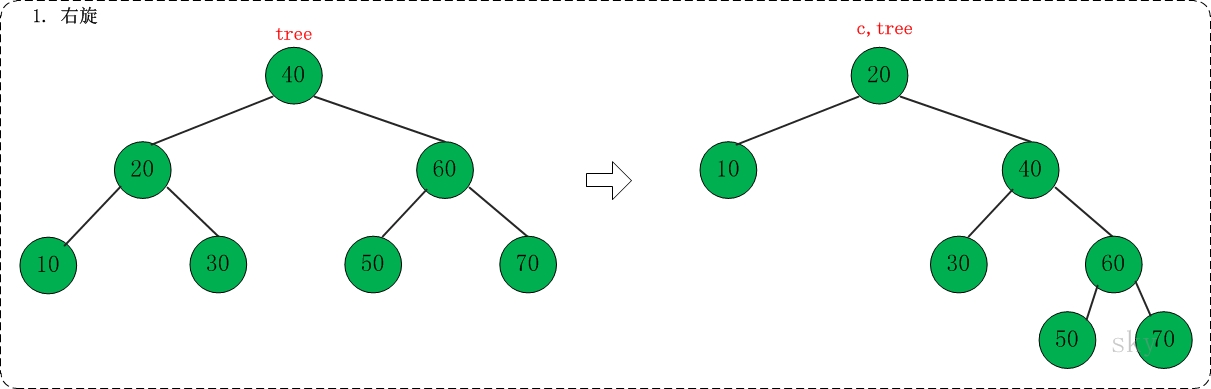
第一步: 右旋
对应代码中的"rotate right"部分
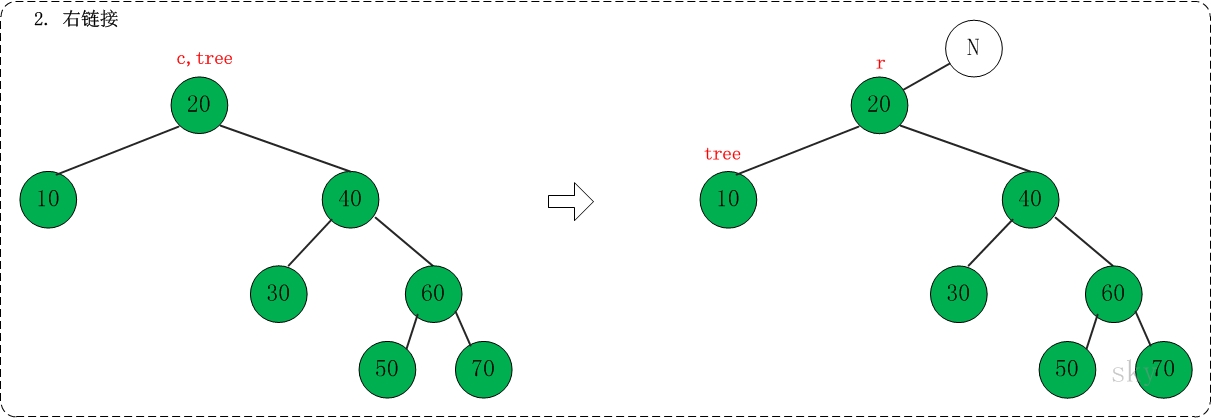
第二步: 右链接
对应代码中的"link right"部分
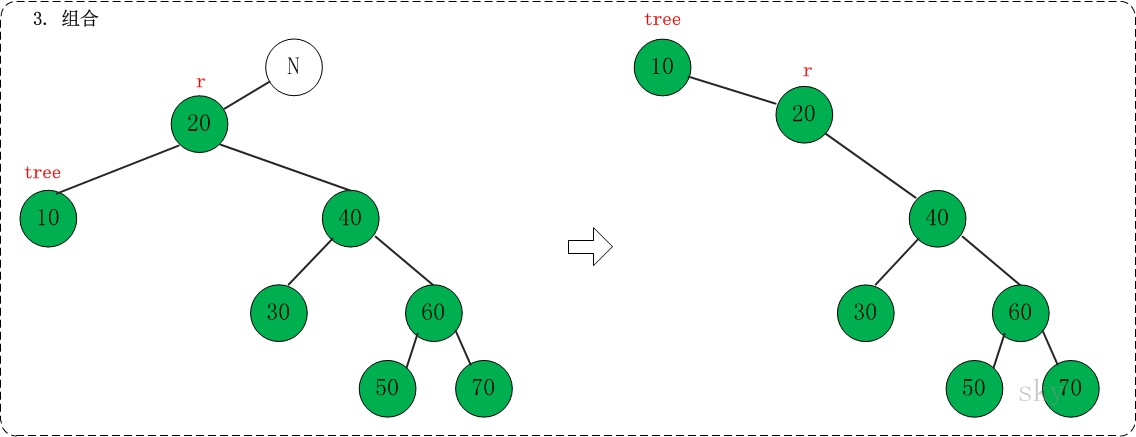
第三步: 组合
对应代码中的"assemble"部分
提示:如果在上面的伸展树中查找"70",则正好与"示例1"对称,而对应的操作则分别是"rotate left", "link left"和"assemble"。
其它的情况,例如"查找15是b-1的情况,查找5是b-2的情况"等等,这些都比较简单,大家可以自己分析。
3. 插入
/* * 将结点插入到伸展树中(不旋转) * * 参数说明: * tree 伸展树的根结点 * z 插入的结点 * 返回值: * 根节点 */ static Node* splaytree_insert(SplayTree tree, Node *z) { Node *y = NULL; Node *x = tree; // 查找z的插入位置 while (x != NULL) { y = x; if (z->key < x->key) x = x->left; else if (z->key > x->key) x = x->right; else { printf("不允许插入相同节点(%d)!\n", z->key); // 释放申请的节点,并返回tree。 free(z); return tree; } } if (y==NULL) tree = z; else if (z->key < y->key) y->left = z; else y->right = z; return tree; } /* * 创建并返回伸展树结点。 * * 参数说明: * key 是键值。 * parent 是父结点。 * left 是左孩子。 * right 是右孩子。 */ static Node* create_splaytree_node(Type key, Node *left, Node* right) { Node* p; if ((p = (Node *)malloc(sizeof(Node))) == NULL) return NULL; p->key = key; p->left = left; p->right = right; return p; } /* * 新建结点(key),然后将其插入到伸展树中,并将插入节点旋转为根节点 * * 参数说明: * tree 伸展树的根结点 * key 插入结点的键值 * 返回值: * 根节点 */ Node* insert_splaytree(SplayTree tree, Type key) { Node *z; // 新建结点 // 如果新建结点失败,则返回。 if ((z=create_splaytree_node(key, NULL, NULL)) == NULL) return tree; // 插入节点 tree = splaytree_insert(tree, z); // 将节点(key)旋转为根节点 tree = splaytree_splay(tree, key); }
外部接口: insert_splaytree(tree, key)是提供给外部的接口,它的作用是新建节点(节点的键值为key),并将节点插入到伸展树中;然后,将该节点旋转为根节点。
内部接口: splaytree_insert(tree, z)是内部接口,它的作用是将节点z插入到tree中。splaytree_insert(tree, z)在将z插入到tree中时,仅仅只将tree当作是一棵二叉查找树,而且不允许插入相同节点。
4. 删除
删除接口
/* * 删除结点(key为节点的键值),并返回根节点。 * * 参数说明: * tree 伸展树的根结点 * z 删除的结点 * 返回值: * 根节点(根节点是被删除节点的前驱节点) * */ Node* delete_splaytree(SplayTree tree, Type key) { Node *x; if (tree == NULL) return NULL; // 查找键值为key的节点,找不到的话直接返回。 if (splaytree_search(tree, key) == NULL) return tree; // 将key对应的节点旋转为根节点。 tree = splaytree_splay(tree, key); if (tree->left != NULL) { // 将"tree的前驱节点"旋转为根节点 x = splaytree_splay(tree->left, key); // 移除tree节点 x->right = tree->right; } else x = tree->right; free(tree); return x; }
delete_splaytree(tree, key)的作用是:删除伸展树中键值为key的节点。
它会先在伸展树中查找键值为key的节点。若没有找到的话,则直接返回。若找到的话,则将该节点旋转为根节点,然后再删除该节点。
注意:关于伸展树的"前序遍历"、"中序遍历"、"后序遍历"、"最大值"、"最小值"、"查找"、"打印"、"销毁"等接口与"二叉查找树"基本一样,这些操作在"二叉查找树"中已经介绍过了,这里就不再单独介绍了。当然,后文给出的伸展树的完整源码中,有给出这些API的实现代码。这些接口很简单,Please RTFSC(Read The Fucking Source Code)!
伸展树的C实现(完整源码)
伸展树的头文件(splay_tree.h)

1 #ifndef _SPLAY_TREE_H_ 2 #define _SPLAY_TREE_H_ 3 4 typedef int Type; 5 6 typedef struct SplayTreeNode { 7 Type key; // 关键字(键值) 8 struct SplayTreeNode *left; // 左孩子 9 struct SplayTreeNode *right; // 右孩子 10 } Node, *SplayTree; 11 12 // 前序遍历"伸展树" 13 void preorder_splaytree(SplayTree tree); 14 // 中序遍历"伸展树" 15 void inorder_splaytree(SplayTree tree); 16 // 后序遍历"伸展树" 17 void postorder_splaytree(SplayTree tree); 18 19 // (递归实现)查找"伸展树x"中键值为key的节点 20 Node* splaytree_search(SplayTree x, Type key); 21 // (非递归实现)查找"伸展树x"中键值为key的节点 22 Node* iterative_splaytree_search(SplayTree x, Type key); 23 24 // 查找最小结点:返回tree为根结点的伸展树的最小结点。 25 Node* splaytree_minimum(SplayTree tree); 26 // 查找最大结点:返回tree为根结点的伸展树的最大结点。 27 Node* splaytree_maximum(SplayTree tree); 28 29 // 旋转key对应的节点为根节点。 30 Node* splaytree_splay(SplayTree tree, Type key); 31 32 // 将结点插入到伸展树中,并返回根节点 33 Node* insert_splaytree(SplayTree tree, Type key); 34 35 // 删除结点(key为节点的值),并返回根节点 36 Node* delete_splaytree(SplayTree tree, Type key); 37 38 // 销毁伸展树 39 void destroy_splaytree(SplayTree tree); 40 41 // 打印伸展树 42 void print_splaytree(SplayTree tree, Type key, int direction); 43 44 #endif
伸展树的实现文件(splay_tree.c)

1 /** 2 * SplayTree伸展树(C语言): C语言实现的伸展树。 3 * 4 * @author skywang 5 * @date 2014/02/03 6 */ 7 8 #include <stdio.h> 9 #include <stdlib.h> 10 #include "splay_tree.h" 11 12 /* 13 * 前序遍历"伸展树" 14 */ 15 void preorder_splaytree(SplayTree tree) 16 { 17 if(tree != NULL) 18 { 19 printf("%d ", tree->key); 20 preorder_splaytree(tree->left); 21 preorder_splaytree(tree->right); 22 } 23 } 24 25 /* 26 * 中序遍历"伸展树" 27 */ 28 void inorder_splaytree(SplayTree tree) 29 { 30 if(tree != NULL) 31 { 32 inorder_splaytree(tree->left); 33 printf("%d ", tree->key); 34 inorder_splaytree(tree->right); 35 } 36 } 37 38 /* 39 * 后序遍历"伸展树" 40 */ 41 void postorder_splaytree(SplayTree tree) 42 { 43 if(tree != NULL) 44 { 45 postorder_splaytree(tree->left); 46 postorder_splaytree(tree->right); 47 printf("%d ", tree->key); 48 } 49 } 50 51 /* 52 * (递归实现)查找"伸展树x"中键值为key的节点 53 */ 54 Node* splaytree_search(SplayTree x, Type key) 55 { 56 if (x==NULL || x->key==key) 57 return x; 58 59 if (key < x->key) 60 return splaytree_search(x->left, key); 61 else 62 return splaytree_search(x->right, key); 63 } 64 65 /* 66 * (非递归实现)查找"伸展树x"中键值为key的节点 67 */ 68 Node* iterative_splaytree_search(SplayTree x, Type key) 69 { 70 while ((x!=NULL) && (x->key!=key)) 71 { 72 if (key < x->key) 73 x = x->left; 74 else 75 x = x->right; 76 } 77 78 return x; 79 } 80 81 /* 82 * 查找最小结点:返回tree为根结点的伸展树的最小结点。 83 */ 84 Node* splaytree_minimum(SplayTree tree) 85 { 86 if (tree == NULL) 87 return NULL; 88 89 while(tree->left != NULL) 90 tree = tree->left; 91 return tree; 92 } 93 94 /* 95 * 查找最大结点:返回tree为根结点的伸展树的最大结点。 96 */ 97 Node* splaytree_maximum(SplayTree tree) 98 { 99 if (tree == NULL) 100 return NULL; 101 102 while(tree->right != NULL) 103 tree = tree->right; 104 return tree; 105 } 106 107 /* 108 * 旋转key对应的节点为根节点,并返回根节点。 109 * 110 * 注意: 111 * (a):伸展树中存在"键值为key的节点"。 112 * 将"键值为key的节点"旋转为根节点。 113 * (b):伸展树中不存在"键值为key的节点",并且key < tree->key。 114 * b-1 "键值为key的节点"的前驱节点存在的话,将"键值为key的节点"的前驱节点旋转为根节点。 115 * b-2 "键值为key的节点"的前驱节点存在的话,则意味着,key比树中任何键值都小,那么此时,将最小节点旋转为根节点。 116 * (c):伸展树中不存在"键值为key的节点",并且key > tree->key。 117 * c-1 "键值为key的节点"的后继节点存在的话,将"键值为key的节点"的后继节点旋转为根节点。 118 * c-2 "键值为key的节点"的后继节点不存在的话,则意味着,key比树中任何键值都大,那么此时,将最大节点旋转为根节点。 119 */ 120 Node* splaytree_splay(SplayTree tree, Type key) 121 { 122 Node N, *l, *r, *c; 123 124 if (tree == NULL) 125 return tree; 126 127 N.left = N.right = NULL; 128 l = r = &N; 129 130 for (;;) 131 { 132 if (key < tree->key) 133 { 134 if (tree->left == NULL) 135 break; 136 if (key < tree->left->key) 137 { 138 c = tree->left; /* 01, rotate right */ 139 tree->left = c->right; 140 c->right = tree; 141 tree = c; 142 if (tree->left == NULL) 143 break; 144 } 145 r->left = tree; /* 02, link right */ 146 r = tree; 147 tree = tree->left; 148 } 149 else if (key > tree->key) 150 { 151 if (tree->right == NULL) 152 break; 153 if (key > tree->right->key) 154 { 155 c = tree->right; /* 03, rotate left */ 156 tree->right = c->left; 157 c->left = tree; 158 tree = c; 159 if (tree->right == NULL) 160 break; 161 } 162 l->right = tree; /* 04, link left */ 163 l = tree; 164 tree = tree->right; 165 } 166 else 167 { 168 break; 169 } 170 } 171 172 l->right = tree->left; /* 05, assemble */ 173 r->left = tree->right; 174 tree->left = N.right; 175 tree->right = N.left; 176 177 return tree; 178 } 179 180 /* 181 * 将结点插入到伸展树中(不旋转) 182 * 183 * 参数说明: 184 * tree 伸展树的根结点 185 * z 插入的结点 186 * 返回值: 187 * 根节点 188 */ 189 static Node* splaytree_insert(SplayTree tree, Node *z) 190 { 191 Node *y = NULL; 192 Node *x = tree; 193 194 // 查找z的插入位置 195 while (x != NULL) 196 { 197 y = x; 198 if (z->key < x->key) 199 x = x->left; 200 else if (z->key > x->key) 201 x = x->right; 202 else 203 { 204 printf("不允许插入相同节点(%d)!\n", z->key); 205 // 释放申请的节点,并返回tree。 206 free(z); 207 return tree; 208 } 209 } 210 211 if (y==NULL) 212 tree = z; 213 else if (z->key < y->key) 214 y->left = z; 215 else 216 y->right = z; 217 218 return tree; 219 } 220 221 /* 222 * 创建并返回伸展树结点。 223 * 224 * 参数说明: 225 * key 是键值。 226 * parent 是父结点。 227 * left 是左孩子。 228 * right 是右孩子。 229 */ 230 static Node* create_splaytree_node(Type key, Node *left, Node* right) 231 { 232 Node* p; 233 234 if ((p = (Node *)malloc(sizeof(Node))) == NULL) 235 return NULL; 236 p->key = key; 237 p->left = left; 238 p->right = right; 239 240 return p; 241 } 242 243 /* 244 * 新建结点(key),然后将其插入到伸展树中,并将插入节点旋转为根节点 245 * 246 * 参数说明: 247 * tree 伸展树的根结点 248 * key 插入结点的键值 249 * 返回值: 250 * 根节点 251 */ 252 Node* insert_splaytree(SplayTree tree, Type key) 253 { 254 Node *z; // 新建结点 255 256 // 如果新建结点失败,则返回。 257 if ((z=create_splaytree_node(key, NULL, NULL)) == NULL) 258 return tree; 259 260 // 插入节点 261 tree = splaytree_insert(tree, z); 262 // 将节点(key)旋转为根节点 263 tree = splaytree_splay(tree, key); 264 } 265 266 /* 267 * 删除结点(key为节点的键值),并返回根节点。 268 * 269 * 参数说明: 270 * tree 伸展树的根结点 271 * z 删除的结点 272 * 返回值: 273 * 根节点(根节点是被删除节点的前驱节点) 274 * 275 */ 276 Node* delete_splaytree(SplayTree tree, Type key) 277 { 278 Node *x; 279 280 if (tree == NULL) 281 return NULL; 282 283 // 查找键值为key的节点,找不到的话直接返回。 284 if (splaytree_search(tree, key) == NULL) 285 return tree; 286 287 // 将key对应的节点旋转为根节点。 288 tree = splaytree_splay(tree, key); 289 290 if (tree->left != NULL) 291 { 292 // 将"tree的前驱节点"旋转为根节点 293 x = splaytree_splay(tree->left, key); 294 // 移除tree节点 295 x->right = tree->right; 296 } 297 else 298 x = tree->right; 299 300 free(tree); 301 302 return x; 303 } 304 305 /* 306 * 销毁伸展树 307 */ 308 void destroy_splaytree(SplayTree tree) 309 { 310 if (tree==NULL) 311 return ; 312 313 if (tree->left != NULL) 314 destroy_splaytree(tree->left); 315 if (tree->right != NULL) 316 destroy_splaytree(tree->right); 317 318 free(tree); 319 } 320 321 /* 322 * 打印"伸展树" 323 * 324 * tree -- 伸展树的节点 325 * key -- 节点的键值 326 * direction -- 0,表示该节点是根节点; 327 * -1,表示该节点是它的父结点的左孩子; 328 * 1,表示该节点是它的父结点的右孩子。 329 */ 330 void print_splaytree(SplayTree tree, Type key, int direction) 331 { 332 if(tree != NULL) 333 { 334 if(direction==0) // tree是根节点 335 printf("%2d is root\n", tree->key); 336 else // tree是分支节点 337 printf("%2d is %2d's %6s child\n", tree->key, key, direction==1?"right" : "left"); 338 339 print_splaytree(tree->left, tree->key, -1); 340 print_splaytree(tree->right,tree->key, 1); 341 } 342 }
伸展树的测试程序(splaytree_test.c)

1 /** 2 * C 语言: 伸展树测试程序 3 * 4 * @author skywang 5 * @date 2014/02/03 6 */ 7 8 #include <stdio.h> 9 #include "splay_tree.h" 10 11 static int arr[]= {10,50,40,30,20,60}; 12 #define TBL_SIZE(a) ( (sizeof(a)) / (sizeof(a[0])) ) 13 14 void main() 15 { 16 int i, ilen; 17 SplayTree root=NULL; 18 19 printf("== 依次添加: "); 20 ilen = TBL_SIZE(arr); 21 for(i=0; i<ilen; i++) 22 { 23 printf("%d ", arr[i]); 24 root = insert_splaytree(root, arr[i]); 25 } 26 27 printf("\n== 前序遍历: "); 28 preorder_splaytree(root); 29 30 printf("\n== 中序遍历: "); 31 inorder_splaytree(root); 32 33 printf("\n== 后序遍历: "); 34 postorder_splaytree(root); 35 printf("\n"); 36 37 printf("== 最小值: %d\n", splaytree_minimum(root)->key); 38 printf("== 最大值: %d\n", splaytree_maximum(root)->key); 39 printf("== 树的详细信息: \n"); 40 print_splaytree(root, root->key, 0); 41 42 i = 30; 43 printf("\n== 旋转节点(%d)为根节点\n", i); 44 printf("== 树的详细信息: \n"); 45 root = splaytree_splay(root, i); 46 print_splaytree(root, root->key, 0); 47 48 // 销毁伸展树 49 destroy_splaytree(root); 50 }
伸展树的C测试程序
伸展树的测试程序运行结果如下:
== 依次添加: 10 50 40 30 20 60 == 前序遍历: 60 30 20 10 50 40 == 中序遍历: 10 20 30 40 50 60 == 后序遍历: 10 20 40 50 30 60 == 最小值: 10 == 最大值: 60 == 树的详细信息: 60 is root 30 is 60's left child 20 is 30's left child 10 is 20's left child 50 is 30's right child 40 is 50's left child == 旋转节点(30)为根节点 == 树的详细信息: 30 is root 20 is 30's left child 10 is 20's left child 60 is 30's right child 50 is 60's left child 40 is 50's left child
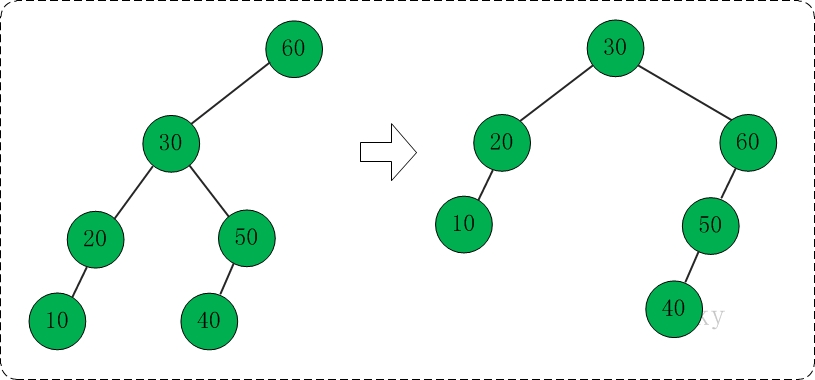
测试程序的主要流程是:新建伸展树,然后向伸展树中依次插入10,50,40,30,20,60。插入完毕这些数据之后,伸展树的节点是60;此时,再旋转节点,使得30成为根节点。
依次插入10,50,40,30,20,60示意图如下:
将30旋转为根节点的示意图如下:






 浙公网安备 33010602011771号
浙公网安备 33010602011771号