转:图像处理之理解卷积
图像处理之理解卷积
一:什么是卷积
卷积公式是用来求随机变量和的密度函数(pdf)的计算公式.
定义式:
z(t)=x(t)*y(t)= ∫x(m)y(t-m)dm.已知x,y的pdf,x(t),y(t).现在要求z=x+y的pdf.我们作变量替显,令
z=x+y,m=x.雅可比行列式=1.那么,z,m联合密度就是f(z,m)=x(m)y(z-m)*1.这样,就可以很容易求Z的在(z,m)中边缘分布
即fZ(z)=∫x(m)y(z-m)dm.
由于这个公式和x(t),y(t)存在一一对应的关系.为了方便,所以记 ∫x(m)y(z-m)dm=x(t)*y(t)
长度为m的向量序列u和长度为n的向量序列v,卷积w的向量序列长度为(m+n-1),
当m=n时,
w(1) = u(1)*v(1)
w(2) = u(1)*v(2)+u(2)*v(1)
w(3) = u(1)*v(3)+u(2)*v(2)+u(3)*v(1)
…
w(n) = u(1)*v(n)+u(2)*v(n-1)+ … +u(n)*v(1)
…
w(2*n-1) = u(n)*v(n)
当m≠n时,应以0补齐阶次低的向量的高位后进行计算
这是数学中常用的一个公式,在概率论中,是个重点也是一个难点.
离散卷积的数学公式可以表示为如下形式:
f(x) = - 其中C(k)代表卷积操作数,g(i)代表样本数据, f(x)代表输出结果。
举例如下:
假设g(i)是一个一维的函数,而且代表的样本数为G = [1,2,3,4,5,6,7,8,9]
假设C(k)是一个一维的卷积操作数, 操作数为C=[-1,0,1]
则输出结果f(x)可以表示为 F=[1,2,2,2,2,2,2,2,1] //边界数据未处理
以上只是一维的情况下,当对一幅二维数字图像加以卷积时,其数学意义可以解释如下:
源图像是作为输入源数据,处理以后要的图像是卷积输出结果,卷积操作数作为Filter
在XY两个方向上对源图像的每个像素点实施卷积操作。如图所示:
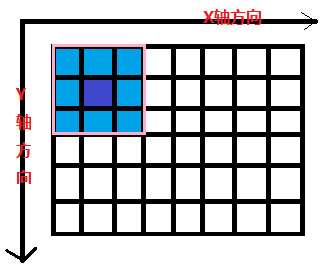
粉红色的方格每次在X/Y前进一个像素方格,就会产生一个新的输出像素,图中正中间深蓝色的代
表要输出的像素方格,走完全部的像素方格,就得到了所有输出像素。
图中,粉红色的矩阵表示卷积操作数矩阵,黑色表示源图像– 每个方格代表一个像素点。
二:卷积在数字图像处理中应用
一副数字图像可以看作一个二维空间的离散函数可以表示为f(x, y), 假设有对于二维卷积操
作函数C(u, v) ,则会产生输出图像g(x, y) = f(x, y) *C(u,v), 利用卷积可以实现对图像模糊处理,边缘检测,产生轧花效果的图像。
一个简单的数字图像卷积处理流程可以如下:
1. 读取源图像像素
2. 应用卷积操作数矩阵产生目标图像
3. 对目标图像进行归一化处理
4. 处理边界像素
三:一个纯Java的卷积模糊图像效果

四:关键代码解释
完成对像素点RGB颜色的卷积计算代码如下:
for( int row = 1;row < srcH-1;row++)
{
for( int col= 1;col< srcW-1;col++)
{
// red color,可以看出卷积核大小为3*3
out3DData[row][col][1] =
in3DData[row][col][1] +
in3DData[row-1][col][1] +
in3DData[row+1][col][1] +
in3DData[row][col-1][1] +
in3DData[row-1][col-1][1] +
in3DData[row+1][col-1][1] +
in3DData[row][col+1][1] +
in3DData[row-1][col+1][1] +
in3DData[row+1][col+1][1];
// green color
out3DData[row][col][2] =
in3DData[row][col][2] +
in3DData[row-1][col][2] +
in3DData[row+1][col][2] +
in3DData[row][col-1][2] +
in3DData[row-1][col-1][2] +
in3DData[row+1][col-1][2] +
in3DData[row][col+1][2] +
in3DData[row-1][col+1][2] +
in3DData[row+1][col+1][2];
// blue color
out3DData[row][col][3] =
in3DData[row][col][3] +
in3DData[row-1][col][3] +
in3DData[row+1][col][3] +
in3DData[row][col-1][3] +
in3DData[row-1][col-1][3] +
in3DData[row+1][col-1][3] +
in3DData[row][col+1][3] +
in3DData[row-1][col+1][3] +
in3DData[row+1][col+1][3];
}
}
计算归一化因子以及对卷积结果归一化处理的代码如下:
// find the peak data frominput and output pixel data.
int inpeak = 0;
int outPeak = 0;
for(int row=0; row<srcH; row++) {
for(int col=0; col<srcW; col++) {
if(inpeak < in3DData[row][col][1]) {
inpeak = in3DData[row][col][1];
}
if(inpeak < in3DData[row][col][2]) {
inpeak = in3DData[row][col][2];
}
if(inpeak < in3DData[row][col][3]) {
inpeak = in3DData[row][col][3];
}
if(outPeak < out3DData[row][col][1]) {
outPeak = out3DData[row][col][1];
}
if(outPeak < out3DData[row][col][2]) {
outPeak = out3DData[row][col][2];
}
if(outPeak < out3DData[row][col][3]) {
outPeak = out3DData[row][col][3];
}
}
}
// normalization
double outputScale = ((double) inpeak) / ((double)outPeak);
for(int row=0; row<srcH; row++) {
for(int col=0; col<srcW; col++) {
out3DData[row][col][1] = (int)(outputScale * out3DData[row][col][1]);
out3DData[row][col][2] = (int)(outputScale * out3DData[row][col][2]);
out3DData[row][col][3] = (int)(outputScale * out3DData[row][col][3]);
}
}
五:本文没有提及的内容 –边界像素处理
没有处理边缘像素,对边缘像素的处理,有两个可以参考的方法
其一是直接填充法– 超出边界部分的以边界像素填充。
其二是线性插值法– 超出边界部分的以 i/row的像素填充。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号