【深度学习】批归一化(Batch Normalization)
BN是由Google于2015年提出,这是一个深度神经网络训练的技巧,它不仅可以加快了模型的收敛速度,而且更重要的是在一定程度缓解了深层网络中“梯度弥散”的问题,从而使得训练深层网络模型更加容易和稳定。所以目前BN已经成为几乎所有卷积神经网络的标配技巧了。
从字面意思看来Batch Normalization(简称BN)就是对每一批数据进行归一化,确实如此,对于训练中某一个batch的数据{x1,x2,...,xn},注意这个数据是可以输入也可以是网络中间的某一层输出。在BN出现之前,我们的归一化操作一般都在数据输入层,对输入的数据进行求均值以及求方差做归一化,但是BN的出现打破了这一个规定,我们可以在网络中任意一层进行归一化处理,因为我们现在所用的优化方法大多都是min-batch SGD,所以我们的归一化操作就成为Batch Normalization。
我们为什么需要BN?
我们知道网络一旦train起来,那么参数就要发生更新,除了输入层的数据外(因为输入层数据,我们已经人为的为每个样本归一化),后面网络每一层的输入数据分布是一直在发生变化的,因为在训练的时候,前面层训练参数的更新将导致后面层输入数据分布的变化。以网络第二层为例:网络的第二层输入,是由第一层的参数和input计算得到的,而第一层的参数在整个训练过程中一直在变化,因此必然会引起后面每一层输入数据分布的改变。我们把网络中间层在训练过程中,数据分布的改变称之为:“Internal Covariate Shift”。BN的提出,就是要解决在训练过程中,中间层数据分布发生改变的情况。
BN怎么做?

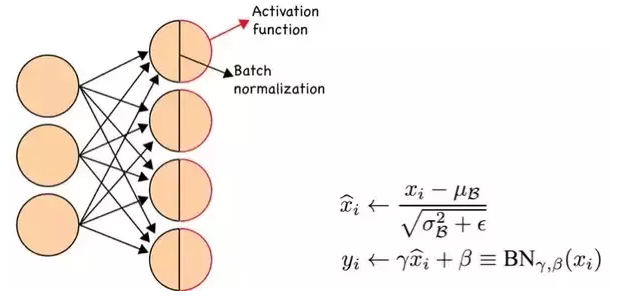
如上图所示,BN步骤主要分为4步:
- 求每一个训练批次数据的均值
- 求每一个训练批次数据的方差
- 使用求得的均值和方差对该批次的训练数据做归一化,获得0-1分布。其中\(\varepsilon\)是为了避免除数为0时所使用的微小正数。
- 尺度变换和偏移:将\(x_{i}\)乘以\(\gamma\)调整数值大小,再加上\(\beta\)增加偏移后得到\(y_{i}\),这里的\(\gamma\)是尺度因子,\(\beta\)是平移因子。这一步是BN的精髓,由于归一化后的\(x_{i}\)基本会被限制在正态分布下,使得网络的表达能力下降。为解决该问题,我们引入两个新的参数:\(\gamma\),\(\beta\)。 \(\gamma\)和\(\beta\)是在训练时网络自己学习得到的。
BN到底解决了什么?
一个标准的归一化步骤就是减均值除方差,那这种归一化操作有什么作用呢?我们观察下图,
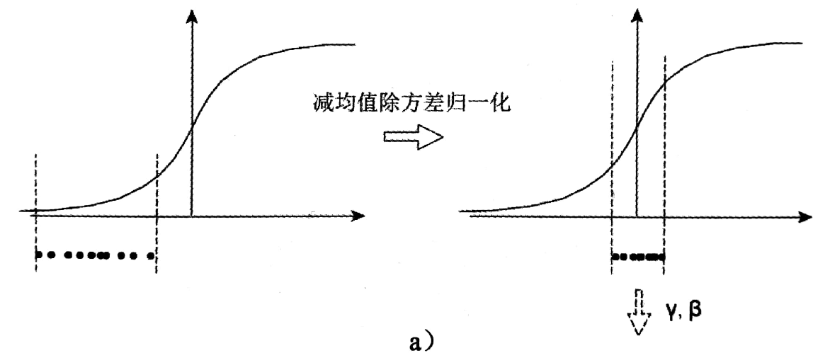

a中左图是没有经过任何处理的输入数据,曲线是sigmoid函数,如果数据在梯度很小的区域,那么学习率就会很慢甚至陷入长时间的停滞。减均值除方差后,数据就被移到中心区域如右图所示,对于大多数激活函数而言,这个区域的梯度都是最大的或者是有梯度的(比如ReLU),这可以看做是一种对抗梯度消失的有效手段。对于一层如此,如果对于每一层数据都那么做的话,数据的分布总是在随着变化敏感的区域,相当于不用考虑数据分布变化了,这样训练起来更有效率。
那么为什么要有第4步,不是仅使用减均值除方差操作就能获得目的效果吗?我们思考一个问题,减均值除方差得到的分布是正态分布,我们能否认为正态分布就是最好或最能体现我们训练样本的特征分布呢?不能,比如数据本身就很不对称,或者激活函数未必是对方差为1的数据最好的效果,比如Sigmoid激活函数,在-1~1之间的梯度变化不大,那么非线性变换的作用就不能很好的体现,换言之就是,减均值除方差操作后可能会削弱网络的性能!针对该情况,在前面三步之后加入第4步完成真正的batch normalization。
BN的本质就是利用优化变一下方差大小和均值位置,使得新的分布更切合数据的真实分布,保证模型的非线性表达能力。BN的极端的情况就是这两个参数等于mini-batch的均值和方差,那么经过batch normalization之后的数据和输入完全一样,当然一般的情况是不同的。
预测时均值和方差怎么求?
在训练时,我们会对同一批的数据的均值和方差进行求解,进而进行归一化操作。但是对于预测时我们的均值和方差怎么求呢?比如我们预测单个样本时,那还怎么求均值和方法呀!其实是这种样子的,对于预测阶段时所使用的均值和方差,其实也是来源于训练集。比如我们在模型训练时我们就记录下每个batch下的均值和方差,待训练完毕后,我们求整个训练样本的均值和方差期望值,作为我们进行预测时进行BN的的均值和方差:

最后测试阶段,BN的使用公式就是:
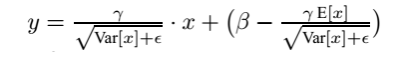
关于BN的使用位置,在CNN中一般应作用与非线性激活函数之前,s型函数s(x)的自变量x是经过BN处理后的结果。因此前向传导的计算公式就应该是:

其实因为偏置参数b经过BN层后其实是没有用的,最后也会被均值归一化,当然BN层后面还有个β参数作为偏置项,所以b这个参数就可以不用了。因此最后把BN层+激活函数层就变成了:

CNN中的BN
注意前面写的都是对于一般情况,对于卷积神经网络有些许不同。因为卷积神经网络的特征是对应到一整张特征响应图上的,所以做BN时也应以响应图为单位而不是按照各个维度。比如在某一层,batch大小为m,响应图大小为w×h,则做BN的数据量为m×w×h。
BN在深层神经网络的作用非常明显:若神经网络训练时遇到收敛速度较慢,或者“梯度爆炸”等无法训练的情况发生时都可以尝试用BN来解决。同时,常规使用情况下同样可以加入BN来加速模型训练,甚至提升模型精度。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号