表示学习

表示学习

这一章聚焦表示学习(Representation Learning)及其应用，主要内容有无监督及有监督预训练的作用，迁移学习及分布式表示。机器学习的主要问题就是如何更合理高效的将特征表示出来。怎么判定某种表示更好呢，这需要具体问题具体分析，这通常依赖于后续的学习任务是否能够得益于这种表示。通常是进行某些无监督学习提取出特征，而这些特征可用来我们更好的进行监督学习，或者将这些特征迁移到其他相关任务中。同时也可以将监督学习训练的前馈神经网络看做是一种表示学习，通常神经网络的最后一层是个分类器如softmax，它之前的隐藏层可以看做是给这个分类器提供一个高效的表征。

在深度学习的再次兴起中，贪心逐层无监督预训练(Greedy Layer-Wise Unsupervised Pretraining)作为无监督学习的代表起了重要的作用，

这其中包括了RBM(restricted boltzmann machine)，单层自编码器，稀疏自编码器等等，它可以通过无监督学习得到输入数据的分布，常常用来提供神经网络的合理的初始值设置。一个常用例子是word embedding，如果我们仅仅用one-hot encoding即用某个元素上为1其他元素为零的向量来表示所有单词的时候，所有的单侧的距离都是相同的 \(\sqrt2\) ，而我们用word embedding将其映射到新的空间，令词义更相近的单词靠得更近，如下图所示。如果我们有某些字符串类型的数据，则利用word embedding可以更有效的表示数据之间的关系。

当然，随着深度学习的发展，无监督预训练重要性逐渐下降，除了自然语言处理外，在其他应用场景如图像识别渐渐被监督预训练所取代，即利用某些在大量有标记图像数据下学习到的公开的较好的配置来初始化我们具体问题的模型。

迁移学习（Transfer Learning)

迁移学习指的是我们将在某种设置下学习到的知识迁移到一个新的领域中，这有点类似于人类举一反三的能力。其基本思想是对于某类任务，其输入或输出遵循一定的基本的共通的规律，学习其中一个则其他任务也可以受益。其中极端的例子是zero-shot learning，即在没有相应的具有标记的数据的情况下进行学习，例如在机器翻译中，假如我们想将X语言中的单词\(A\)翻译成\(Y\)语言中的单词\(B\)，而我们并没有直接的将\(X\)中\(A\)对应到\(Y\)中\(B\)单词的训练数据，但我们之前已经得到了\(A\)在\(X\)中的表征，\(B\)在\(Y\)中的表征，假如我们学习过\(X\)与\(Y\)的表征空间的映射（例如我们只需要一些\(X\)和\(Y\)中哪些句子是成对的数据而不需要单词一一对应的数据即可学习这种映射），则我们可以推断\(A\)的对应的翻译\(B\)。

分布式表示(Distributed Representation)

分布式表示的概念 ( 由很多元素组合的表示, 这些元素之间可以设置成可分离的 ) 是表示学习最重要的工具之一。分布式表示非常强大, 因为他们能用具有 \(k\) 个值的 \(n\) 个特征去描述 \(k^n\) 个不同的概念。正如在本书中看到的, 具有多个隐藏单元的神经网络和具有多个潜变量的概率模型都利用了分布式表示的策略。现在再介绍一个观察结果。许多深度学习算法基于的假设是, 隐藏单元能够学习表示出解释数据的潜在因果因子。这种方法在分布式表示上是自然的, 因为表示空间中的每个方向都对应着一个不同的潜在配置变量的值。
\(n\) 维二元向量是一个分布式表示的示例, 有 \(2^n\) 种配置, 每一种都对应输入空间中的一个不同区域。这可以与符号表示相比较, 其中输入关联到单一符号或类别。如果字典中有 \(n\) 个符号, 那么可以想象有 \(n\) 个特征监测器, 每个特征探测器监测相关类别的存在。在这种情况下, 只有表示空间中 \(n\) 个不同配置才有可能在输入空间中刻画 \(n\) 个不同的区域。这样的符号表示也被称 为 one-hot 表示, 因为它可以表示成相互排斥的 \(n\) 维二元向量 (其中只有一位是激活的)。符号表示是更广泛的非分布式表示类中的一个具体示例, 它可以包含很多条目，但是每个条目没有显著意义的单独控制作用。下图为分布式表示：

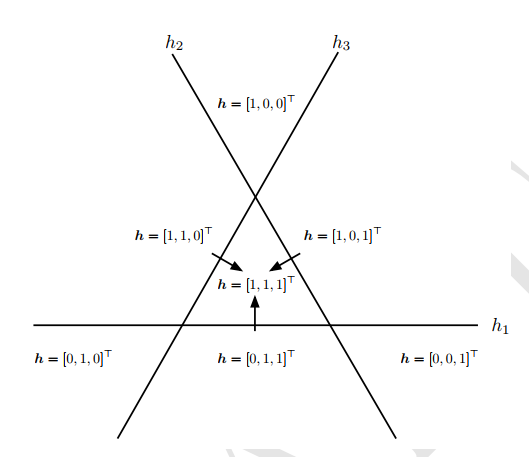
下图为符号表示：

以下是基于非分布式表示的学习算法的示例:

• 聚类算法, 包含 k-means 算法: 每个输入点恰好分配到一个类别。

• \(k\)-最近邻算法: 给定一个输入, 一个或几个模板或原型样本与之关联。在 \(k>1\) 的情况下, 每个输入都使用多个值来描述, 但是它们不能彼此分开控制, 因此 这不能算真正的分布式表示。

• 决策树: 给定输入时, 只有一个叶节点 (和从根到该叶节点路径上的点) 是被激活的。

• 高斯混合体和专家混合体: 模板 (聚类中心) 或专家关联一个激活的程度。和 \(k\)-最近邻算法一样, 每个输入用多个值表示, 但是这些值不能轻易地彼此分开控制。

• 具有高斯核（或其他类似的局部核）的核机器：尽管每个“支持向量”或模板样本的激活程度是连续值, 但仍然会出现和高斯混合体相同的问题。

• 基于 \(n\)-gram 的语言或翻译模型: 根据后缀的树结构划分上下文集合（符号序列 )。例如, 一个叶节点可能对应于最后两个单词 \(w_1\) 和 \(w_2\) 。树上的每个叶节点分别估计单独的参数 (有些共享也是可能的)。

不可否认的是，之前很多的无监督学习方法有一定的局限性，比如常常需要设定特定的优化目标，比如均方差尽量小，这决定了哪些特征可以是显著的特征而忽略了其他特征。例如图像合成领域某些局域的对比度变化不高的图案会被忽略掉。所以Ian提出了生成对抗网络(Generative Adversarial Network）简称GAN，这个在第20章会详细总结，其基本思想就是我们训练生成模型取欺骗另一个分类器，而分类器则是尽量提高能区分出我们的生成模型与真实的训练数据的准确度。这样两个模型都不断改进，并且能提取所有的关键信息而不产生遗漏。如下图中所示，采用均方差为训练目标的传统无监督学习的合成图像会丢失掉耳朵的信息，而GAN合成的图像则可以以假乱真。

回到最初的问题，怎样判定某种表示优于另一种表示呢? 这里总结一些大致的指导思想，当然具体问题还需要选取合适的判定条件：

• 平滑: 假设对于单位 \(\boldsymbol{d}\) 和小量 \(\epsilon\) 有 \(f(\boldsymbol{x}+\epsilon \boldsymbol{d}) \approx f(\boldsymbol{x})\) 。这个假设允许学习器从训练样本泛化到输入空间中附近的点。许多机器学习算法都利用了这个想法, 但它不能克服维数灾难难题。

• 线性: 很多学习算法假定一些变量之间的关系是线性的。这使得算法能够预测远离观测数据的点, 但有时可能会导致一些极端的预测。大多数简单的学习算法不会做平滑假设, 而会做线性假设。这些假设实际上是不同的, 具有很 大权重的线性函数在高维空间中可能不是非常平滑的。

• 多个解释因子: 许多表示学习算法受以下假设的启发, 数据是由多个潜在解释因子生成的, 并且给定每一个因子的状态, 大多数任务都能轻易解决。学习 \(p(x)\) 的结构要 求学习出一些对建模 \(p(\boldsymbol{y} \mid x)\) 同样有用的特征, 因为它们都涉及到相同的潜在解释因子。

• 因果因子：该模型认为学成表示所描述的变差因素是观察数据 \(\boldsymbol{x}\) 的成因, 而并非反过来。这对于半监督学习是有利的, 当潜在成因上的分布发生改变, 或者我们应用模型到一个新的任务上时, 学成的模型会更加鲁棒。

• 深度，高级抽象概念能够通过将简单概念层次化来定义。从另一个角度来看, 深度架构表达了我们认为任务应该由多个程序步骤完成的观念, 其中每一个步骤回溯到先前步骤处理之后的输出。

• 任务间共享因素: 当多个对应到不同变量 \(\mathrm{y}_i\) 的任务共享相同的输入 \(\mathrm{x}\) 时, 或者当每个任务关联到全局输入 \(\mathrm{x}\) 的子集或者函数 \(f^{(i)}(\mathbf{x})\) 时, 我们会假设每个变量 \(\mathrm{y}_i\) 关联到来自相关因素 \(\mathrm{h}\) 公共池的不同子集。因为这些子集有重叠, 所以通过共享的中间表示 \(P(\mathbf{h} \mid \mathbf{x})\) 来学习所有的 \(P\left(\mathrm{y}_i \mid \mathbf{x}\right)\) 能够使任务间共享统 计强度。

• 流形: 概率质量集中, 并且集中区域是局部连通的, 且占据很小的体积。在连续情况下, 这些区域可以用比数据所在原始空间低很多维的低维流形来近似。很多机器学习算法只在这些流形上有效。一些机器学习算法, 特别是自编码器, 会试图显式地学习流形的结构。

• 自然聚类：很多机器学习算法假设输入空间中每个连通流形可以被分配一个单独的类。数据分布在许多个不连通的流形上, 但相同流形上数据的类别是相同的。这个假设激励了各种学习算法, 包括正切传播、双反向传播、流形正切分类器和对抗训练。

• 时间和空间相干性：慢特征分析和相关的算法假设, 最重要的解释因子随时间 变化很缓慢, 或者至少假设预测真实的潜在解释因子比预测诸如像素值这类原 始观察会更容易些。

• 稀疏性: 假设大部分特征和大部分输入不相关, 如在表示猫的图像时, 没有必要使用象鼻的特征。因此, 我们可以强加一个先验, 任何可以解释为 “存在” 或 “不存在” 的特征在大多数时间都是不存在的。

• 简化因子依赖: 在良好的高级表示中, 因子会通过简单的依赖相互关联。最简 单的可能是边缘独立, 即 \(P(\mathbf{h})=\prod_i P\left(\mathbf{h}_i\right)\) 。但是线性依赖或浅层自编码器所能表示的依赖关系也是合理的假设。这可以从许多物理定律中看出来, 并且假设在学成表示的顶层插入线性预测器或分解的先验。

总的来说学习数据的更好表示是一个仍需大量深入研究的课题。不仅仅是深度学习，在线性代数，高等代数，复变函数中的多种数学分解，也可以理解为改进数据或者函数的数学表示，从而帮助我们进行后续的处理。而这又与算法的先验紧紧相关，天下没有白吃的午餐，所以对于不同的问题，我们需要选择合理的表示和表示学习法。