批量梯度下降

批量梯度下降

本文主要介绍了在深度学习优化中遇到的问题以及解决方法，在此简要地记录核心的部分。

Stochastic Gradient Descent（随机梯度下降）

在数值计算中，书本介绍了Gradient Descent算法，但是在实际使用中，梯度下降计算梯度时需要利用所有的数据样本，其优点是这样计算的梯度较为准确，但缺点是在样本量大的情况下计算量较大。

假设我们有n个样本，其均值的标准差为 \(\sigma\) ，其中 \(\frac{\sigma}{\sqrt{n}}\) 是MLE的真实标准差。我们可以看到，分母是 \(\sqrt{n}\) 表明随着样本的增多，计算梯度的准确度的回报是小于线性的。例如我们有两种方法：1. 利用100个样本计算梯度 2.利用10000个样本计算梯度。 第二种方法是第一种的100倍的计算量，但只将均值的标准差减少了10倍，我们通常希望我们能更快的达到我们的优化目标，所以不需要每次计算梯度都严格的利用全部样本，而是进行多次iteration，而每次估算的梯度有合适的准确度即可。在优化算法里，我们通常把一次仅利用一个样本来更新的方式叫做stochastic或online方法。但对于深度学习来讲，我们通常所说的stochastic gradient descent指的是minibatch stochastic methods，即每次计算梯度时利用一部分样本，其样本量是新引入的超参数batch size。随机梯度下降算法参数更新规则如下表示：

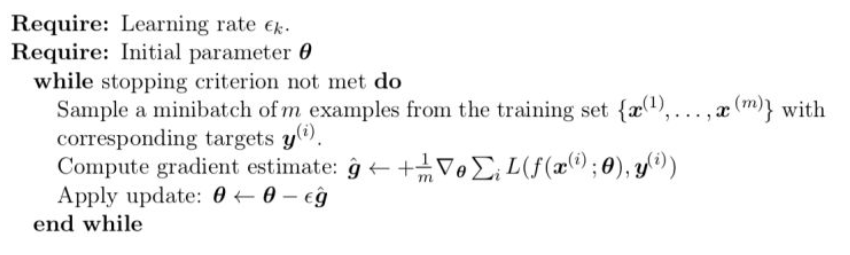
tips: 随机梯度下降在第一次样本的迭代过程中可以看作是在求解真实数据生成分布 \(\mathit{p} _{data}\)对\(\mathit{p} _{model}(y|x)\)的交叉熵损失函数梯度 $-\mathbb{E}_{\mathbf{x,y}\sim \mathit{p} _{data}}\bigtriangledown _{\theta}\log\mathit{p} _{model}(y|x) $ 的无偏估计，其学习对象是泛化误差而非训练误差。因为从模型的角度上来说，每次取mini batch 的时候是从数据流得到数据的，而数据流是来自真实的数据分布 \(\mathit{p}_{data}\)，因此随机梯度下降的泛化能力更好。从图进行解释，就是SGD算法相比与GD算法，更容易随机地在函数曲面进行移动，相比于GD每次固定下降的梯度，SGD更容易跳出一些局部最小值点。

注意到，我们引入了另一个超参数学习率 \(\epsilon_k\) ，可以说学习率是深度学习中最重要的需要调节的参数，如果学习率过大，我们可能会一次就跳过极小点而到山谷的另一侧，那么训练的loss可能会有较大波动而不是一致的向极小点步进，另一方面，如果学习率过小，训练更新过小，需要较长时间才能达到较好效果。通常我们需要经过不断的试验来选取合适的学习率，另外也可以在初始时使用稍大一些的学习率，随着训练的进行可以逐步的降低学习率从而避免波动，例如通常采用的方法是对于前 \(\tau\) 次iteration, 线性的降低学习率 \(\epsilon_k=\left(1-\frac{k}{\tau}\right) \epsilon_0+\frac{k}{\tau} \epsilon_\tau\)，之后保持学习率恒定。
但是，对于SGD，常常会遇到一个问题：病态的Hessian矩阵。Hessian在条件数非常大的时候，会使得函数在各个方向上的曲率区别非常大，此时在使用SGD算法时，较短的步长也会导致函数值不降反升，或者下降的路径曲折蜿蜒，非常影响效率，如下图所示：

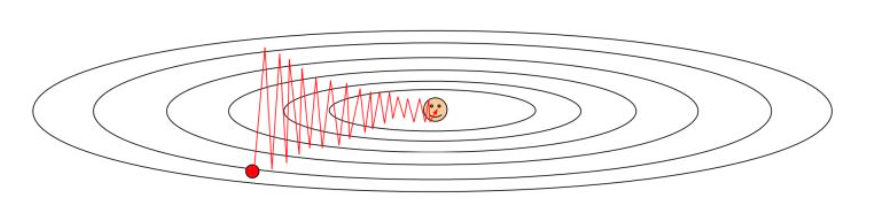
所以为了改进算法的性能，人们提出了几种改进梯度下降算法。

Momentum（动量）

Momentum，顾名思义，来自物理学中的动量概念，即我们用一个新的变量 \(v(v\) 可以看做是速度，在质量为单位质量时大小等于Momentum) 来记录之前的梯度变化的速度，其优势在于对于 局域极小值或鞍点的情况，由于保持了原有的速度，模型可以继续更新。
更新法则用公式表示为

\[\begin{aligned} & v \leftarrow \alpha v-\epsilon \nabla_\theta\left(\frac{1}{m} \sum_{i=1}^m L\left(f\left(x^{(i)} ; \theta\right), y^{(i)}\right)\right) \\ & \theta \leftarrow \theta+v \end{aligned} \]

其中 \(\alpha\) 表示了之前的梯度的贡献衰减的速率，如果 \(\alpha\) 相对于 \(\epsilon\) 越大，则之前的梯度对当前方向影响越大。与SGD比较，可以看出原SGD只要梯度大步进幅度较大，而对于Momentum来说，如果之前若干次梯度方向一致，才有较大的步进幅度。受Nesterov加速算法的启发，后续人们还提出了Nesterov动量的随机梯度下降算法。其与动量的SGD只有一个区别，就是在计算梯度的时候进行了下一步的梯度预测，所以更加保守。

到此为止，学习算法依旧是在对梯度进行改进，而对于每一轮的学习，其学习率则采用常数。虽然对梯度进行改进确实改进了算法性能，但是同时也增加了新的超参数，那么我们自然会想到能否对学习率这个超参数进行学习。但是以下三种方法均是自适应学习率(Adaptive learning rate)的算法，即随着模型进行自我调控学习率并对于不同的参数采取不同的学习率。

AdaGrad

与Momentum方法比较，AdaGrad没有引入速度变量 \(v\) ，而是记录每个参数方向上的梯度的值的平方和，在该参数方向上步进时除以这个平方和的平方根，则对于原梯度较小学习进展较慢的方向相较于原梯度较大的方向rescale的程度较小，从而加速在该方向上的学习进程。其具体的更新规则为：

其中 \(\odot\) 为元素乘积符号，即对于每个元素求平方，其输出结果为矢量。矢量 \(r\) 即为每个参数方向 的梯度平方和的积累值，注意我们对其做除法时会假如一个极小量 \(\delta\) 以防除数为零的情况发生。

RMSProp

Adagrad虽然可以较好的解决不同方向曲率差异过大的情况，但是我们可以看到随着训练的进行， 除数 \(\sqrt{r}\) 在不断增大，学习率衰减依赖于所有之前的梯度的历史结果，可能在我们末达到极值点 前学习率已经减至过低从而无法有效的更新模型。所以RMSProp方法在其上做了改进，即对于 \(r\) 加入一定的衰减，使较早的梯度贡献较小，即我们计算的是一个带有指数权重的moving average。其更新法则与AdaGrad不同的地方在于

Adam

Adam 可以看做是RMSProp 与Momentum方法的一种结合，其得名于Adaptive moments，意在结合两者的优点。它引入两个moment, 第一个即为速度的Momentum，第二个moment则是如RMSProp中的梯度的平方和，并分别对两个moment进行一些随时间变化的修正。其更新法则如下：

Adam算法对梯度的一阶矩和二阶矩进行了修正，使其成为无偏估计量，相比于使用动量的RMSProp算法，其避免了二阶矩的高偏置，拥有更好的鲁棒性。