浅谈扫描线
前言
之前在qbxt听lxl讲课的时候,一直在强调扫描线很重要,知道学了之后才明白这东西好用归好用,难写归难写。
预备知识
线段树,平衡树,各种数据结构,离线询问……
概念
因为有很多题我们难以直接分析出性质,再加之人类本身就有几何直观性,因此,扫描线就诞生了。
再说说扫描线,就是将问题中一些关键点放到平面上的一种思路。
其实扫描线的本质就是将静态的二维问题变成动态的一维问题。
还是放在例题里将比较明白吧……
不算例题的例题
二维数点,可以在 \(O(n log n)\) 内解决
考虑构建平面,将点放在上面。
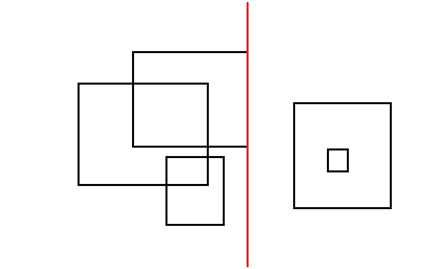
然后将每个询问看做在平面上的矩形查询,那么就会如图:
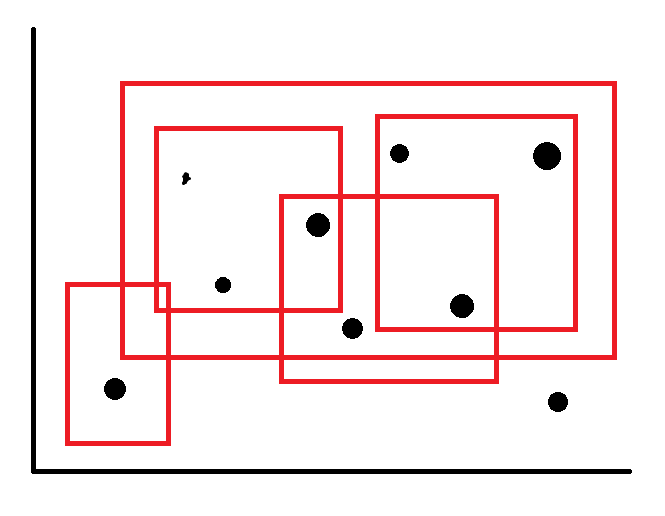
但是发现好像不太好做一个 \(4-side\) 矩形的查询
那就差分,把一个 \(4-side\) 矩形差分成4个 \(2-side\) 矩形,就很好处理了。
和上面的数据不一样,但是还是看看图吧
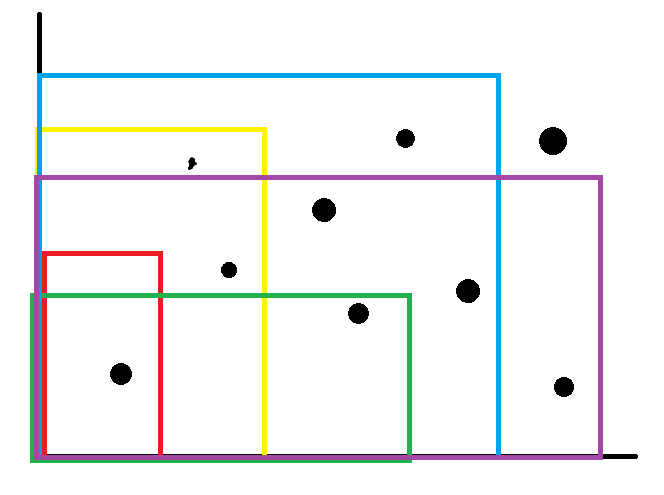
然后想有一根线从左扫到右边,那根线是一个什么随便一个数据结构,每遇到一个点就单点加,遇到一条边就区间查,最后合并答案,就算完了。
差不多图长这样:
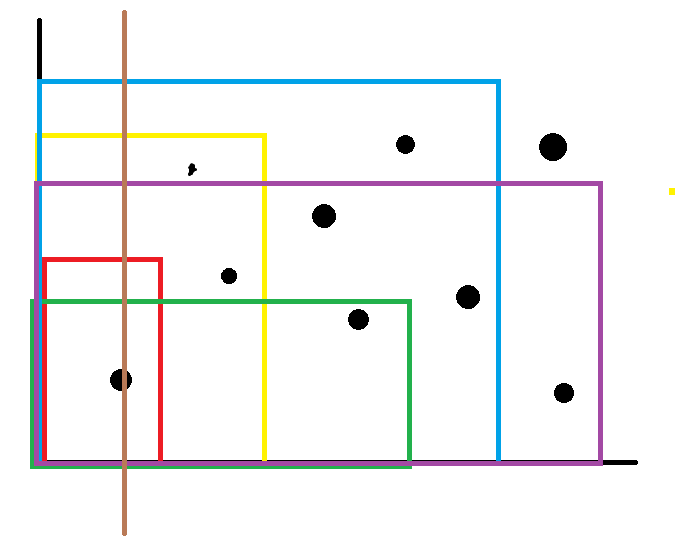
不算例题的例题+1
求每个点被多少个给定的\(n\)个矩形包含,可以在 \(O(n log n)\) 内解决
大概就是这样,考虑使用扫描线,将每个矩形的左边界和右边界分开处理,左边区间加,右边区间减,遇见点的时候单点查询。
例题1
简化版题意:静态的区间数颜色
看到这道题,我们不难想到一个莫队解法,但是与本题没什么关系,现在可能也过不去了。
首先,我们不难得出一个性质:区间内如果一个颜色是第一次出现,那么他上一次出现必然在区间外。
这个看起来很显然的性质能够有大用。
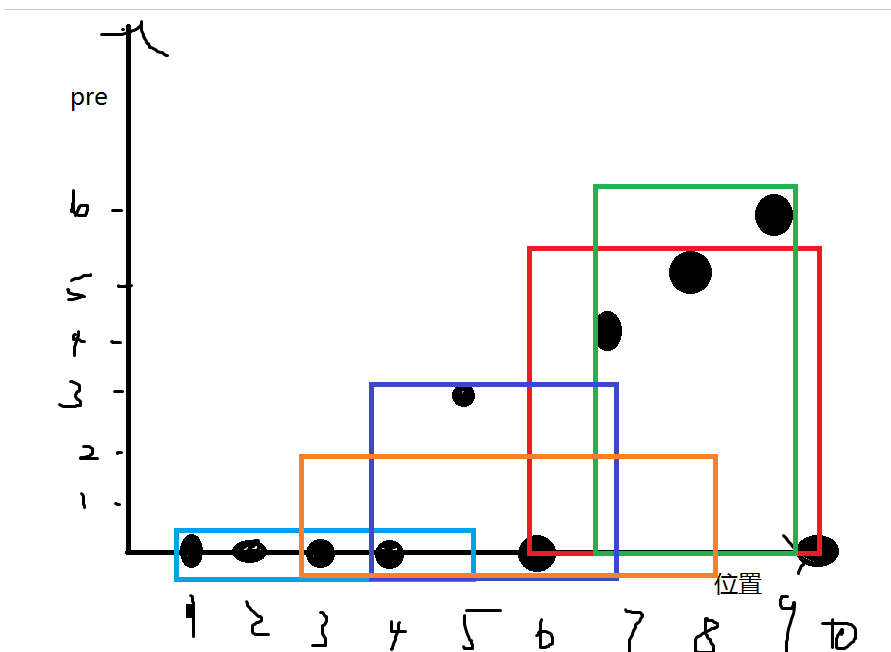
这个时候,我们发现每一个元素有两维,一个是位置,一个是前驱的位置。
将他们放到平面上,就转化成了一个二维数点问题,也可以仿照上面的那个东西,把\(3-side\)矩形差分成2个\(2-side\)矩形,之后可以拿扫描线解决,具体看下图。
数据:
4 6 5 2 5 1 2 5 1 7
6 10
7 9
1 5
4 7
3 8
例题2
经典问题:矩形面积并
离散化什么的都是小问题,先不考虑那些有的没的,就假设离散化完了或者不用离散化。
考虑把这种矩形并给分开来算,就是分割矩形,大体来说,就是用扫描线扫横坐标,数据结构维护纵坐标。
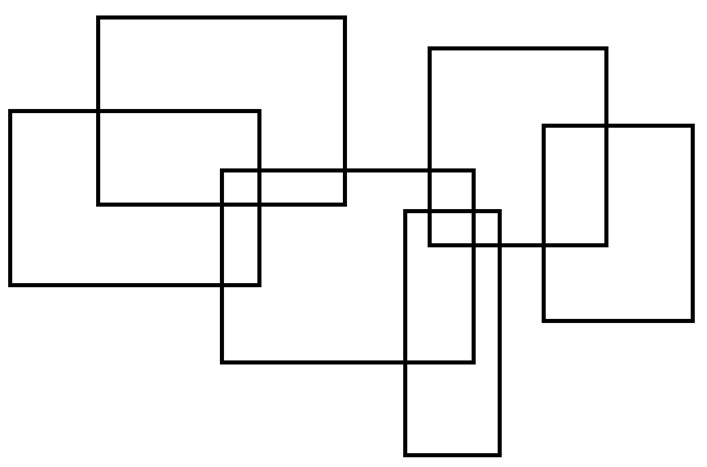
分割之后:

接下来问题来了,怎么用数据结构维护纵坐标呢?
还是相似地考虑,走到矩形左边时区间加,右边时区间减,那维护答案时就是 全局非零值的个数 \(\times\) 两根线的宽度
如何维护全局非零个数?
使用线段树,对于每一个节点,我们维护最小值和最小值个数,在合并时,如果最小值不同,取较小值,然后继承较小值那边的个数;如果最小值相等,那么就直接把个数相加
在最后,我们检验最小值是否是零就可以维护了qwq
例题3
给定许多模式字符串,然后查询时每次给你两个字符串s1,s2,问你这一堆模式串里有多少个串满足前缀是s1,后缀是s2的
来一个 \(O(\left| S \right| + (m+n)logn)\) 的做法
见到了前缀,后缀,字符串,不妨考虑一下我们可爱的 \(trie\) 树
我们建两棵 \(trie\) 树,一棵叫 \(T1\) ,用来正着插入那一堆模式串,还有一棵叫 \(T2\) ,用来倒着插入那一堆模式串
之后我们不难发现,如果对于一个模式串 \(S1\) ,它的前缀可以在 \(T1\) 里面找,后缀可以在 \(T2\) 里面找。
那么对于询问时给出的那两个字符串,如果前一个在 \(T1\) 中匹配到的地方dfs序是 \(l1,r1\) ,后一个在 \(T2\) 中匹配到的地方dfs序是 \(l2,r2\),那么就有一个结论
满足题目条件的字符串的首字符的dfs序和末尾字符的dfs序必然在 \(l1,r1\) 和 \(l2,r2\)中
那么考虑把他们放到平面上,每一个字符串代表的点的横坐标就是他在 \(T1\) 中的dfs序,纵坐标就是他在 \(T2\) 中的dfs序
每一次询问都是一个二维数点了qwq
例题4
题意很简单,现就不考虑强制在线的版本,我也不会说的……
我们不妨换个角度去说这个东西,不去考虑询问时怎么办,而是考虑每个元素会对可能的答案产生什么贡献
那么这个时候,我们就想一想元素怎么出现,区间怎么分布,可能会产生贡献
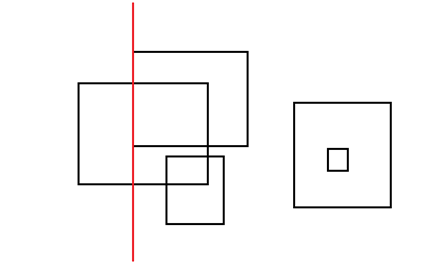
如下图
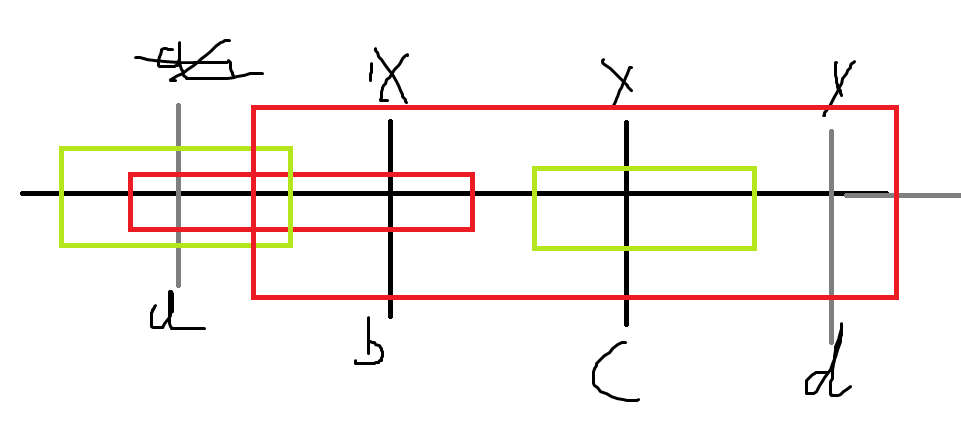
在 \(a,b,c,d\) 处都出现了 \(x\) 那么可以发现,只有绿框的情况下会产生贡献,红框是不行的
那么绿框的范围是相邻的两个区间,也就是左端点在一个区间,右端点在一个区间
同时,绿框的数量是 \(n\) 的
把它放到二维平面内,就变成了 \(n\) 次矩形加, \(m\) 次单点查,形同点矩形包含


 浙公网安备 33010602011771号
浙公网安备 33010602011771号