279. Perfect Squares

一、题目

　　1、审题

　　

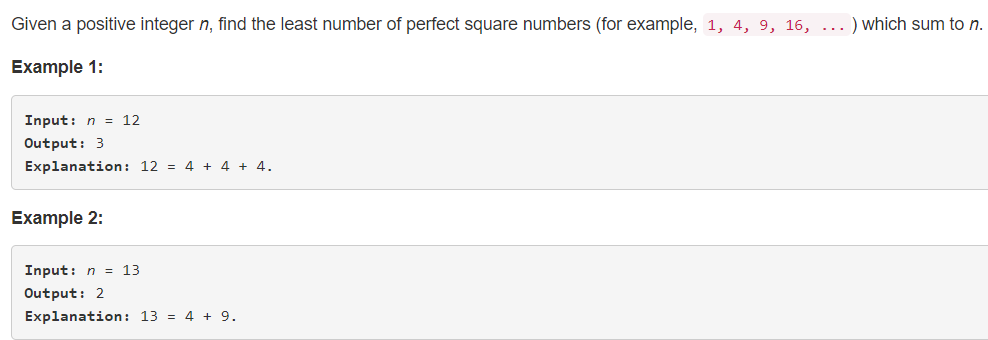
　　2、分析

　　　　给出正整数 n，判断 n 由几个平方数的和构成。

 

二、解答

　　1、思路

　　　　方法一、

　　　　　　动态规划！

　　　　　　①、创建大小为 n + 1 的数组。其中，初始化时 dp[0] = 0,其他元素值为 Integer.Max_VALUE。

　　　　　　②、之后，依次给 dp 从 1 开始的下标元素进行赋值。采用  dp[i] = dp[i - j *j] + 1; 即通过前面的元素值来推断出后面的元素值。

　　　　　　③、返回 dp[n];

    public int numSquares(int n) {
        int[] dp = new int[n + 1];
        Arrays.fill(dp, Integer.MAX_VALUE);
        dp[0] = 0;
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j * j <= i; j++) {
                dp[i] = Math.min(dp[i], dp[i - j * j] + 1);
            }
        }
        return dp[n];
    }

 

　　方法二、

　　　　 Legendre's  四平方定理；

　　　　根据这一定理： 任意一个正整数，可以用不超过 4 个平方和的数来表示。其中：

　　　　用 1 个平方和表示： n = A * A;

　　　　用 2 个平方和表示： n = A * A + B * B;

　　　　用 4 个平方和表示： n = 4^k*(8*m + 7)； 能用这种方式表示；

　　　　用 3 个平方和表示： 其他。

    public int numSquares2(int n) {
        // If n is a perfect square, return 1.
        if(is_square(n))
            return 1;
        
        // The result is 4 if and only if n can be written in the 
        // form of 4^k*(8*m + 7). Please refer to 
        // Legendre's three-square theorem.
        while((n & 3) == 0) // n%4 == 0  
            n >>= 2;
        
        if((n & 7) == 7)    // n%8 == 7
            return 4;
        
        // Check whether 2 is the result.
        int sqrt_n = (int)Math.sqrt(n);
        for (int i = 1; i <= sqrt_n; i++) {
            if(is_square(n - i * i))
                return 2;
        }
        
        return 3;
    }
    
    public boolean is_square(int n) {
        int sqrt_n = (int)(Math.sqrt(n));
        return sqrt_n * sqrt_n == n; 
    }