动态区间求和

遇到问题，寻求解决问题的博客：Xenny

这里简单的随笔，是想整理一份自己看得懂的资料

---

题目描述：
请编写程序对数组a1​,a2​,...,an​进行如下操作 ：
1 i x：给定i,x，将ai​ 加上x ；
2 l r：给定l,r，求al​+al+1​+...+ar​的值。

解决方法：

（1）树状数组

关键：lowbit()

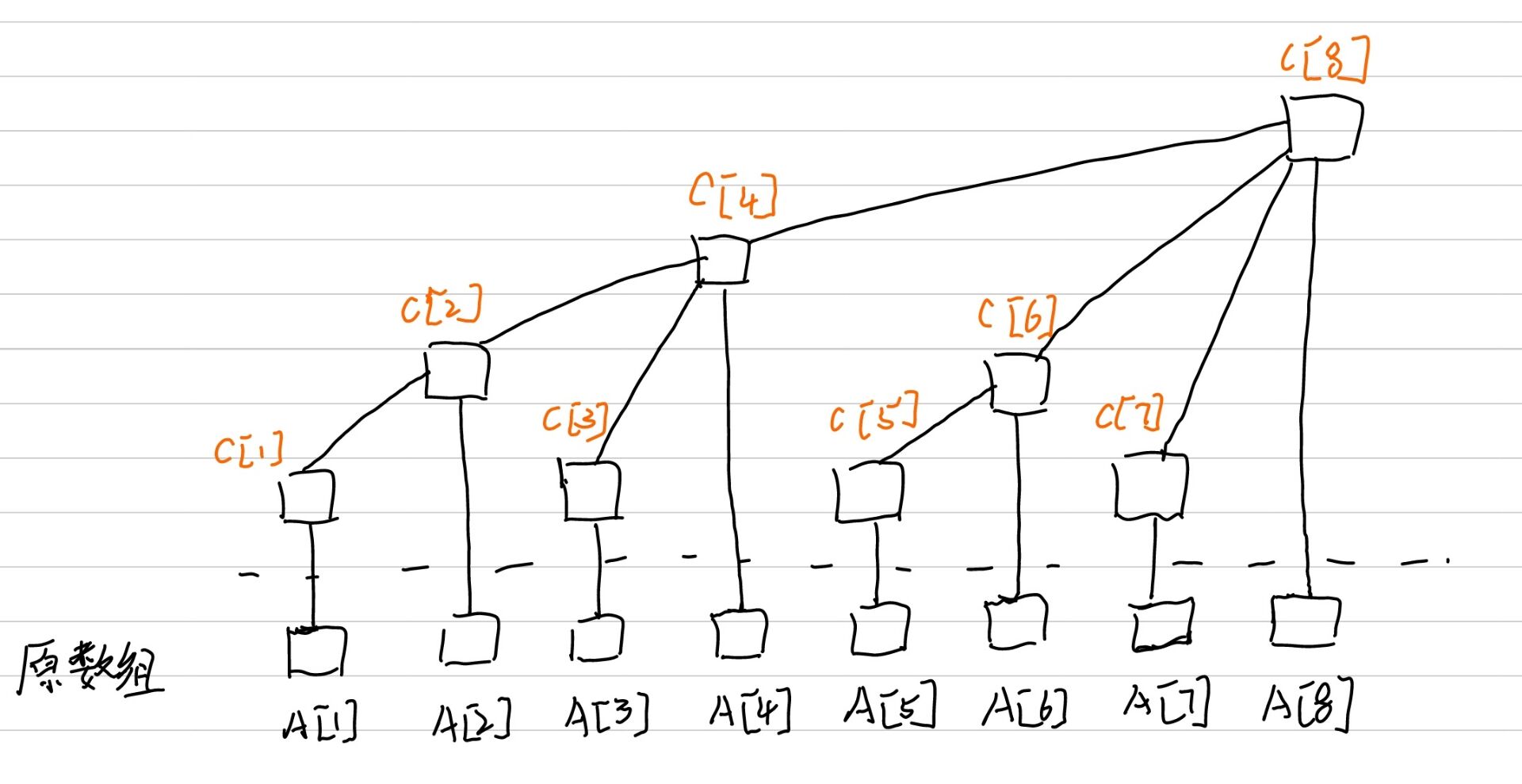
在数组表示树的前提下，每个节点通过一定的规则来表示一段区间（根据具体要求可以将其改为最小值，最大值，和），通过少部分区间的修改来得到答案。
更新时需要注意的规则：C[i] = A[i - 2k+1] + A[i - 2k+2] + ... + A[i];   //k为i的二进制中从最低位到高位连续零的长度

求和时需要注意的规则：

而根据上面的式子，容易的出SUMi = C[i] + C[i-2k1] + C[(i - 2k1) - 2k2] + .....；其中2k中的k表示的就是当前这个位置的i的二进制中从最低位到高位连续的0的长度。
求法
可以为

  int lowbit(const int& i){
  　　return i&(-i);
  }

解决问题的代码：

int lowbit(const int& set) {
  return set & (-set);
}
void update(const int& set, const int& mod) {
  for (int k = set; k <= number; k += lowbit(k)) {
    tree_array[k] += mod;
  }
}
long long getsum(int var) {
  sum = 0;
  while (var)
  {
    sum += tree_array[var];
    var -= lowbit(var);
  }
  return sum;
}

---

以上就是树状数组最基本的应用

---

但是这种只是一种问题（单点更新，区间求和的一个实例）

那么类似的问题分为一下几类：

（1）单点更新，单点查询

直接数组应用

（2）单点更新，区间查询

正是这种区间求和问题，树状数组基本应用

（3）区间更新，区间查询

已有基础上可能想到的方法：
1，普通数组，一个个加，
2，树状数组（在只学完求和的基础上），也是在区间里一个个改变，还没1快，多余操作太多

利用树状数组改进方法：

利用差分和

普通数组存储的是这个值和前一个值的差，树状数组中原本应该存值的和，现在存储差分的和

也就是说通过差分构建树状数组：

就是把update(const int& set,const int& value); 中的value改为a[i]-a[i-1]
其它的就和求和代码一样了

（4）区间更新，单点查询：：

∑ni = 1A[i] = ∑ni = 1 ∑ij = 1D[j];

则A[1]+A[2]+...+A[n]

= (D[1]) + (D[1]+D[2]) + ... + (D[1]+D[2]+...+D[n])

= nD[1] + (n-1)D[2] +... +D[n]

= n * (D[1]+D[2]+...+D[n]) - (0D[1]+1D[2]+...+(n-1)*D[n])

所以上式可以变为∑ni = 1A[i] = n∑ni = 1D[i] -  ∑ni = 1( D[i](i-1) );

所以维护两个树状数组：：第一个每个节点：D[i]，第二个每个节点：D[i]*(i-1)

代码：

#include<iostream>
using namespace std;
const int len = 1e5 + 2;
int array_raw[len];
long long tree_array1[len], tree_array2[len];
int N;
long long num;
int lowbit(const int& i) {
  return i & (-i);
}
void update(const int& set, const int& var) {
  for (int i = set; i <= N; i += lowbit(i)) {
    tree_array1[i] += var;
    tree_array2[i] += var * (set - 1);
  }
}
long long getnum(const int& set) {
  num = 0;
  for (int i = set; i>0; i -= lowbit(i)) {
    num += (set*tree_array1[i] - tree_array2[i]);
  }
return num;
}
int main() {
  int Q;
  cin >> N >> Q;
  int var;
  for (int i = 1; i <= N; i++) {
  cin >> array_raw[i];
    update(i, array_raw[i]-array_raw[i-1]);
  }
  int var2,var1;
  char varr;
  while (Q--)
  {
    cin >> varr;
    cout << "***" << varr << endl;
    switch (varr)
    {
      case 'C': {
        cin >> var >> var1 >> var2;
        update(var,var2);
        update(var1 + 1, -var2);
        break;
       }
    case 'Q': {
        cin >> var1 >> var2;
        cout << getnum(var2) - getnum(var1 - 1) << endl;
        break;
      }
    }
  }
  return 0;
}

（2）线段树

那为什么有了树状数组还要有线段树呢， 线段树比二叉树解决的问题更为广泛，我看到的树状数组解决的是区间的更新以及求和问题，但是线段树可以区间的更新，求和，求最大值，求最小值，等更多问题。