CDQ && 珂朵莉树

对于题目：P4690 [Ynoi2016] 镜中的昆虫我们零基础从各个小部分开始学习，并且 A 了 Ta.

Part 1 CDQ分治

一看到这个东西，一定会觉得很吓人，觉得是什么高大上的东西。其实不然，且听我慢慢讲来。

先明白 ta 是用来干什么的，解决三维偏序。三维偏序是什么？

给定一个命题 $j$ Ta 有三个属性不妨设为

$pos_{j_1} \enspace pos_{j_2} \enspace pos_{j_3}$

问所有满足条件的命题 $i$ 对 $j$ 的贡献是什么。（$i$ 也一样与 $j$ 有三个对应的属性）

所谓满足条件，就是这三个对应的属性同时满足指定的大小关系。

（关于模型的扩展后面会将 >w<）

有点抽象？上模板！

【模板】三维偏序（陌上花开）

题目背景

这是一道模板题，可以使用 bitset，CDQ 分治，KD-Tree 等方式解决。

题目描述

有 $ n $ 个元素，第 $ i $ 个元素有 $ a_i,b_i,c_i $ 三个属性，设 $ f(i) $ 表示满足 $ a_j \leq a_i $ 且 $ b_j \leq b_i $ 且 $ c_j \leq c_i $ 且 $ j \ne i $ 的 $j$ 的数量。

对于 $ d \in [0, n) $，求 $ f(i) = d $ 的数量。

输入格式

第一行两个整数 $ n,k $，表示元素数量和最大属性值。

接下来 $ n $ 行，每行三个整数 $ a_i ,b_i,c_i $，分别表示三个属性值。

输出格式

$ n $ 行，第 $ d + 1 $ 行表示 $ f(i) = d $ 的 $ i $ 的数量。

样例 #1

样例输入 #1

样例输出 #1

提示

$ 1 \leq n \leq 10^5$，$1 \leq a_i, b_i, c_i \le k \leq 2 \times 10^5 $。
————————————————————————————————————————————

可以发现，我们先前所说的三个元素，在这里分别表示 $a, b, c$。

而所谓的大小关系在这一道题里面全都表现为 $ \ge$

那么考虑如何解决这个问题。

暴力的做法就是一个一个枚举去比较，同时满足三个条件的就计入答案。

这是三个“愿望” 一次满足。

那么我们一个一个去满足 “愿望” 呢？

发现：三个约束条件在地位上是等价的，也就是说先满足哪个都无所谓。这里我选择满足的顺序为 $a, b, c$

先考虑 $a$
直接 $sort$ 按 $a$ 的大小排序，这样直接搞定第一个条件。

sort(tmp + 1, tmp + 1 + n, com);

现在我们排序好了！

再考虑后面两个条件，并不是很好处理。于是CDQ分治就出现了！

首先我们假设要处理的序列长度为 $n$

定义 $mid = (1 + n) / 2$。

将该序列分为

$[1, mid], [mid + 1， n]$ 两个序列

先看看能不能快速计算前面一个序列对后面一个序列里的每个元素贡献。

显然，后面一个序列任意一个元素的 $a$ 一定是大于等于任意一个前面一个序列元素的 $a$。对于 $a$ 的约束条件直接略去，不看。
（$a$：是不是不爱我了 qwq）

两部分都对 $b$ 满足的条件去 $sort$ 根据上面的依据，两个队列这样排序完之后对 “前序列对后序列元素”的贡献并无影响。

现在我们再一次排序好了！

这是候我们使用两个指针 $L$ 和 $R$ 起始位置

$L = 1, R = mid + 1$

对于$R$ 每指到一个数字，我们一直将 $b_L \le b_R$ 的数放入备选区并且使 $L$ 指针向后移动($L ++$ )，直到 $L > mid \enspace || \enspace b_L < b_R$。这时候，再从备选区中统计 $R$ 的答案。统计完之后 $R$指针向后移动($R ++$)，直到 $R == n$.

由于之前排过序的原因， $L$ 一直往前，备选区里面的元素始终都会满足当前 $R$ 的 $b$ 条件。于是现在完成了两个“愿望”

现在考虑如何统计备选区的元素如何统计进答案。

假设当前备选区中有 $k$ 个元素，那么对于 $R$ 的贡献为 $\sum\limits_{i = 1}^k [c_i \le c_R]$, 直接使用权值树状数组去搞。（这应该很容易想到吧（雾））。

mid = (1 + n) >> 1;
int L = 1, R = mid + 1; //这是两个指针的起始位置
for(; R <= n; R ++){
while(L <= m && a[L].b <= a[R].b) Add(a[L].val, 1), L ++；//插入树状数组并且移动指针。
ans[a[R].id/*答案编号*/] += Query(a[R].c);
}

现在我们统计完了答案，发现成功的求出了前一个区间对后一个区间里元素的贡献。这当然是不够的，发现对于任意一个区间都可以进行类似的操作，于是我们分而治之，直接递归处理。

先在不是对于区间$[1, n]$, 而是更一般的 $[l, r]$
只要修改一下变量即可

$mid = (l + r) >> 1$
$L = l, R = mid + 1$

递归的底层就是 $l == r$

别忘了递归下去做的时候把树状数组清空！

正确性先感性理解一发，举例序列原长为 $9$，看看哪些元素对 $7$ 有贡献。由于对 $a$ 的限制，那么 $8 \sim 9$是不会对 $7$ 有贡献的。

开始分治（qwq）

第一次对 $[1, 9]: [1, 5]$ $[6, 9]$ 那么计算了 $[1, 5]$ 对 $7$ 的贡献

之后$[1, 5]$ 对 $7$ 没有影响了，直接跳过不去看他

第二次对 $[6, 9]: [6, 7]$ $[8, 9]$

对 $7$ 无影响，之后对于 $7$ , $[8, 9]$也无用了

第三次对 $[6, 7] : [6, 6] [7, 7]$ 计算了 $[6, 6]$ 对 $7$ 的贡献。

递归结束。

综上，我一共统计了 $[1, 6]$ 对 $7$ 的贡献！正好是我们暴力所作的 >w<

上代码：（可能变量申明会有所不同）

#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int tr[N];
int l_ans[N];
struct T{
	int a, b, c, ans, cnt;
}cd[N], tmp[N];

int bs(int x){
	return x & (-x); 
}
void clear(){
	memset(tr, 0, sizeof(tr));
}

int n, k;

bool com(T x, T y){
	if(x.a == y.a && x.b == y.b)
		return x.c < y.c;
	if(x.a == y.a)
		return x.b < y.b;
	return x.a < y.a;
}

void Add(int x, int val){
	while(x <= k){
		tr[x] += val;
		x += bs(x);
	}
	return ;
}

int query(int x){
	int ans = 0;
	while(x > 0){
		ans += tr[x];
		x -= bs(x); 
	}
	return ans;
}


bool com1(T x, T y){
	if(x.b == y.b)
		return x.c < y.c;
	return x.b < y.b;
}
void cdq(int l, int r){
	if(l == r) return;//到头就直接run
	int mid = (l + r) >> 1;
	cdq(l, mid), cdq(mid + 1, r);//先递归处理两边qqq 
	sort(cd + l, cd + mid + 1, com1);
	sort(cd + mid + 1, cd + r + 1, com1);
	
	int L = l, R = mid + 1;
	for(; R <= r; R ++){
		while(L <= mid && cd[L].b <= cd[R].b)
			Add(cd[L].c, cd[L].cnt), L ++;
		cd[R].ans += query(cd[R].c); 
	}
	for(int i = l; i < L; i ++)
		Add(cd[i].c, -cd[i].cnt);
		
	return;
}
int main(){
	scanf("%d%d", &n, &k);
	for(int i = 1; i <= n; i ++){
		scanf("%d%d%d", &tmp[i].a, &tmp[i].b, &tmp[i].c);
//		tmp[i].id = i;
	}
//	tmp[n + 1] = {-114514, -1919810, -190307, 0};	
	sort(tmp + 1, tmp + 1 + n, com);
	int tot = 0;
	int m = 0;
	for(int i = 1; i <= n; i ++){
		tot ++;
		if(tmp[i].a != tmp[i + 1].a || tmp[i].b != tmp[i + 1].b || tmp[i].c != tmp[i + 1].c){//这边是合并了同类元素
			cd[++ m] = tmp[i];
			cd[m].cnt = tot;
			tot = 0;
		}
	}
	cdq(1, m); 
	
	for(int i = 1; i <= m; i ++)
		l_ans[cd[i].ans + cd[i].cnt - 1] += cd[i].cnt;
	
	for(int i = 0; i < n; i ++)
		printf("%d\n", l_ans[i]);
	
	return 0;
}

这是模板，你可能觉得没有什么用，但是如果我告诉你 Ta 可以把动态的问题静态话呢？
将动态问题静态化，在我看来是CDQ分治最迷人的地方。

先上一道题。

[CQOI2011]动态逆序对

题目描述

对于序列 $a$，它的逆序对数定义为集合

\[\{(i,j)| i<j \wedge a_i > a_j \} \]

中的元素个数。

现在给出 $1\sim n$ 的一个排列，按照某种顺序依次删除 $m$ 个元素，你的任务是在每次删除一个元素之前统计整个序列的逆序对数。

输入格式

第一行包含两个整数 $n$ 和 $m$，即初始元素的个数和删除的元素个数。
以下 $n$ 行，每行包含一个 $1 \sim n$ 之间的正整数，即初始排列。
接下来 $m$ 行，每行一个正整数，依次为每次删除的元素。

输出格式

输出包含 $m$ 行，依次为删除每个元素之前，逆序对的个数。

样例 #1

样例输入 #1

样例输出 #1

提示

【数据范围】
对于 $100\%$ 的数据，$1\le n \le 10^5$，$1\le m \le 50000$。

【样例解释】
删除每个元素之前的序列依次为：

\[1,5,3,4,2 \]

\[1,3,4,2 \]

\[3,4,2 \]

\[3,2 \]

————————————————————————————————————————————
在思考这道题前，先回忆一下逆序对满足的条件是什么。
对于两个数 $j$ 以及 $i$。
从 $j$ 的视角来看。（$pos_j$ 指的是 $j$ 的下标）。

若 $j < i \enspace \&\& \enspace pos_j > pos_i$ 那么 $i, j$ 构成逆序对

若 $i < j \enspace \&\& \enspace pos_j < pos_i$ 那么 $i, j$ 也构成逆序对

那么现在我们对于一个命题就拥有了两个约束条件。

对了！这是动态问题，题目会不断地删元素。
我们将每一次查询和修改看作一个又一个时间点，那么对于每一个数都可能在某一个时间点消失（删除操作）
如果我们把一个数的 “存活时间” 记录下来，那么这时候如果 $i$ 对 $j$ 有贡献那么一定要 $time_i \ge time_j$。这个贡献是在时间段 $[1, time_j]$都存在的。我们可以将这样的贡献暂且存储在 $val[time_j]$ 中，当我们处理完所有时间点后取一发前缀和就能搞定（后缀和？）

现在我们回过头来再看看一共的条件:

\[j < i \enspace \&\& \enspace pos_j > pos_i \enspace or \enspace i < j \enspace \&\& \enspace pos_j < pos_i \]

\[time_i \ge time_j \]

没错，每一组正好三个约束条件，直接上三维偏序的模板。
但是这里又有一点不一样，对于 “或上” 的两个条件在每次区间到元素统计答案的时候分开来一组一组做。
这样就完成了本题。这么看来是不是就体会到了动态转静态的神奇用法？
上代码：

#include <bits/stdc++.h>
using namespace std;
#define ll long long
int n, m;
const int N = 1e5 + 1145; 
struct T{
	int time, id, val;
}cd[N];
int mp[N];

ll ans_time[N];
ll tr[N];
ll ans[N];

int lb(int x){
	return x & (-x);
}

void Add(int x, int val){
	while (x <= n){
		tr[x] += val;
		x += lb(x);
	}
}

ll Que(int x){
	ll ans = 0;
	while (x){
		ans += tr[x];
		x -= lb(x);
	}
	return ans;
}

bool com1(T a, T b){ //时间第一关键字， id第二关键字， val第三关键字 
	if(a.time == b.time)
		return a.id < b.id;
	return a.time < b.time;
}

bool com2(T a, T b){
	return a.id < b.id;
} 

void cdq(int l, int r){
	if(l == r) return ;
	int mid = (l + r) >> 1;
	cdq(l, mid);
	cdq(mid + 1, r);
	sort(cd + l, cd + mid + 1, com2);
	sort(cd + mid + 1, cd + r + 1, com2);
	
	int L = l, R = mid + 1;
	for(; R <= r; R ++){//这里只是 id > && val >  
		 
		while(L <= mid && cd[L].id <= cd[R].id )
			Add(cd[L].val, 1), L ++;
		ans_time[-cd[R].time] += Que(cd[R].val); 
//		cout << Que(cd[R].val) << endl;
	}
	for(int i = l; i < L; i ++)
		Add(cd[i].val, -1);
//分开来统计两次答案——————————————————————————————————————
	L = mid;
	R = r;
	for(; R > mid; R --){
		while(L >= l && cd[L].id >= cd[R].id)
			Add(cd[L].val, 1), L --;
		ans_time[-cd[R].time] += Que(n) - Que(cd[R].val - 1);
	}
	
	for(int i = mid; i > L; i --)
		Add(cd[i].val, -1);
	
	return ;
}
int main(){
	scanf("%d%d", &n, &m);
	
	for(int i = 1; i <= n; i ++){
		scanf("%d", &cd[i].val);
		mp[cd[i].val] = i;
		cd[i].time = - m;
		cd[i].id = -i; //这样的话就转化为了纯纯的三位偏序题目 
	}
	
	for(int i = 1; i <= m; i ++){
		int v;
		scanf("%d", &v);
		cd[mp[v]].time = -i;
	} //那么现在 一个玩意儿有贡献就是 'time' i > 'time' j &&  val i > val j && 'id' i > id 'j'   那么对于 <= (- 'time' i 的时候， i的贡献都是成立的） 
	//这边取负号相当于是改变的不等号的方向， 并不是一定要取的qwq
	sort(cd + 1, cd + 1 + n, com1);
	
	cdq(1, n);
	
	ans[m + 1] = 0;
	for(int i = m; i >= 1; i --)
		ans[i] = ans[i + 1] + ans_time[i];
	for(int i = 1; i <= m;i ++)
		printf("%lld\n", ans[i]);
		 
	return 0;
}

到这里我们是不是可以举一反三。
由此我们得到了三维偏序建模的技巧。
（其实没有什么技巧）：构造出合理的三个属性，然后直接套模板。

对了, 三位偏序还有一个经典的模型 ————二维数点。
虽然这玩意儿也可以用树套树来做，但是树套树在某些题目中会使空间爆炸，就像下面一道题

[BOI2007]Mokia 摩基亚

题目描述

摩尔瓦多的移动电话公司摩基亚（Mokia）设计出了一种新的用户定位系统。和其他的定位系统一样，它能够迅速回答任何形如“用户 C 的位置在哪？”的问题，精确到毫米。但其真正高科技之处在于，它能够回答形如“给定区域内有多少名用户？”的问题。

在定位系统中，世界被认为是一个 $w×w$ 的正方形区域，由 $1\times 1$ 的方格组成。每个方格都有一个坐标 $(x,y)$，$1\leq x,y\leq w$。坐标的编号从 $1$ 开始。对于一个 $4\times 4$ 的正方形，就有 $1\leq x\leq 4$，$1\leq y\leq 4$（如图）：

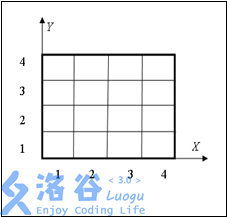
请帮助 Mokia 公司编写一个程序来计算在某个矩形区域内有多少名用户。

输入格式

有三种命令，意义如下：

命令	参数	意义
$0$	$w$	初始化一个全零矩阵。本命令仅开始时出现一次。
$1$	$x\,y\,a$	向方格 $(x,y)$ 中添加 $a$ 个用户。$a$ 是正整数。
$2$	$x1\,y1\,x2\,y2$	查询 $x1\leq x\leq x2$，$y1\leq y\leq y2$ 所规定的矩形中的用户数量。
$3$	无参数	结束程序。本命令仅结束时出现一次。

输入共若干行，每行有若干个整数，表示一个命令。

输出格式

对所有命令 $2$，输出一个一行整数，即当前询问矩形内的用户数量。

样例 #1

样例输入 #1

样例输出 #1

3
5

提示

数据规模与约定

对于 $100\%$ 的数据，保证：

$1\leq w\leq 2000000$。
$1\leq x1\leq x2\leq w$，$1\leq y1\leq y2\leq w$，$1\leq x,y\leq w$，$0<a\leq 10000$。
命令 $1$ 不超过 $160000$ 个。
命令 $2$ 不超过 $10000$ 个。
————————————————————————————————————————————
将操作分成两部分，查询和修改。

现在我们对于一个修改 $i$ 和一个查询 $j$。

我们还是先切成一个又一个时间点来做。
看看再什么时候 $i$ 会对 $j$ 有贡献

\[time_i < time_j \]

\[x_{j_1} \le x_i \le x_{j_2} \]

\[y_{j_1} \le y_i \le y_{j_2} \]

这三个条件显然不好处理，不妨利用二维前缀和的思想把每一个 $j$ 拆开为四个查询。

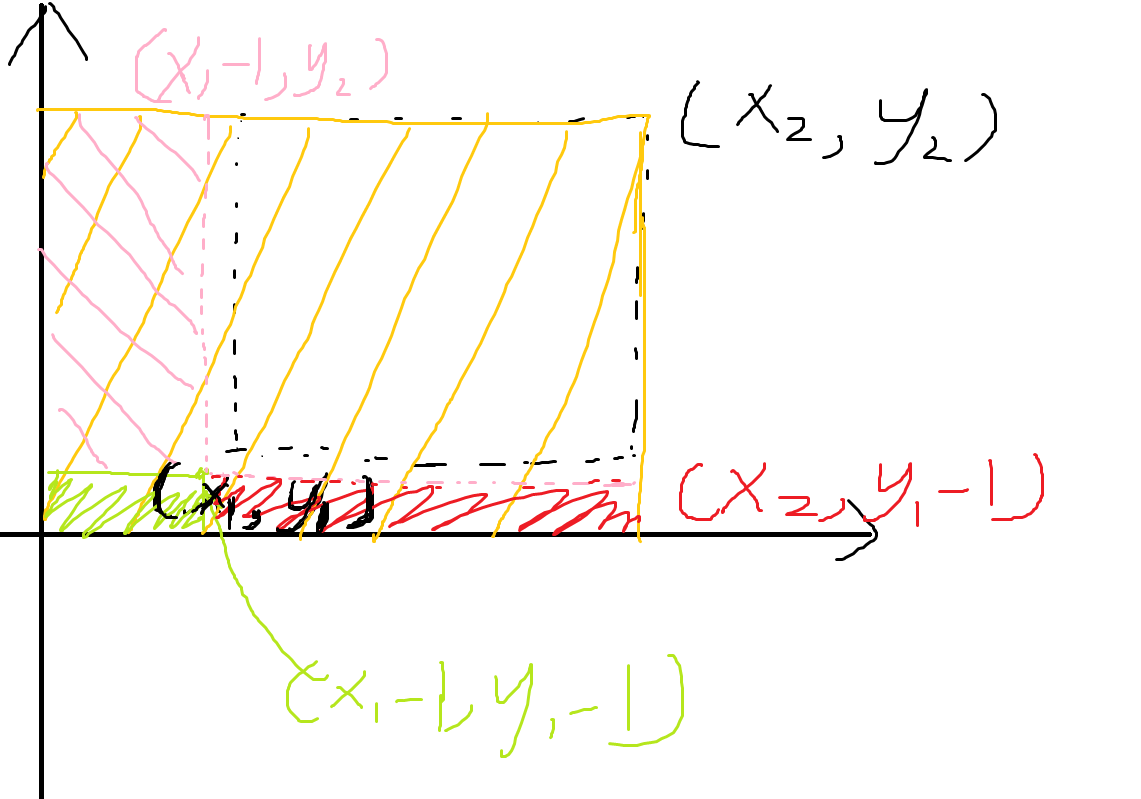
我们对于每一个拆开来的查询只要满足

\[time_i < time_{j'} \]

\[x_i \le x_{j'} \]

\[y_i \le y_{j'} \]

就可以产生贡献，最后合并一下就可以了！（如上图：$ans_j = ans_{yellow} + ans_{green} - ans_{res} - ans_{pink}$）

我们又回到了三维偏序！

注意在计算价值的时候只有修改才有可能对查询产生贡献
上代码

#include <bits/stdc++.h>
using namespace std;
const int N = 2e7 + 1130;
const int M = 2e5 + 1123;
const int inf = 0x3f3f3f3f;
#define ll long long
ll la_ans[M];
//看两个参数 i, j 当time_i < time_j的时候， 同时 x_i <= x_j && y_i <= y_j 那么i这个修改对于j这个查询有贡献。 
//这是什么？ 三维偏序！！！ 直接二分时间乱搞 
//tim为第一关键字， x为第二关键字， y为第三关键字 
struct trr{
	int val[N], up;
	int lb (int x) {return x & (-x);}
	void Add(int x, ll va) {
		while (x <= up)
			val[x] += va,
			x += lb(x);
	}
	ll Que(int x){
		ll ans = 0;
   		while(x)
   			ans += val[x],
   			x -= lb(x);
   		return ans;
	} 
}tr;

struct T{
	int x, y;//[x], [y]
	bool pos, way;//[pos : 1 修改 / 0 查询] [way ：对答案的贡献形式]
	ll id, cnt; //[cnt :修改时的量/ 查询的价值] [id : 对答案编号的贡献] 
	int tim;//[tim : 出现的时间] 
}cd[M];

int n, m;

bool com1(T a, T b){
	if(a.tim == b.tim){
		if(a.x == b.x)
			return a.y < b.y;
		return a.x < b.x; 
	}
	return a.tim < b.tim;
} 

bool com2(T a, T b){
	if(a.x == b.x)
		return a.y < b.y;
	return a.x < b.x;
} 

void solve(int l, int r){
	if(l == r)  return;
	int mid = (l + r) >> 1;
	solve(l, mid), solve(mid + 1, r); //两边处理一下 
	sort(cd + l, cd + mid + 1, com2);
	sort(cd + mid + 1, cd + r + 1, com2);

	int L = l, R = mid + 1;
	for(; R <= r; R ++){
		if(cd[R].pos) continue; //这里要统计的是答案， 修改这种东西直接跳过
		
		while(L <= mid && cd[L].x <= cd[R].x){ //保证 x 的合法性 
			if(!cd[L].pos) {L ++;continue;} //这里要修改，  查询什么的不要啦 >w< 
			tr.Add(cd[L].y, cd[L].cnt);//类似于权值树状数组 
			L ++; 
		}
		cd[R].cnt += tr.Que(cd[R].y); //累加答案 
	}
	for(int i = l; i < L; i ++)
		if(cd[i].pos)
			tr.Add(cd[i].y, -cd[i].cnt); //清空 |>w<|
	return ; 
}
int main(){
	int tot = 0;
	int time = 0;
	int ii = 0; 
	while(1){
		int pos, x_1, x_2, y_1, y_2, va;
		scanf("%d", &pos);
		if(pos == 3) break;
		switch(pos){
			case 0 : 
				scanf("%d", &x_1);
				tr.up = x_1;
				break;
			case 1 :
				time ++;
	                        scanf("%d%d%d", &x_1, &y_1, &va);
				cd[++ tot] = {x_1, y_1, true, false, -1, va, time};
				break;
			case 2 :
				time ++;
				ii ++;
				scanf("%d%d%d%d", &x_1, &y_1, &x_2, &y_2);
				cd[++ tot] = {x_2, y_2, false, 1, ii, 0, time};
				cd[++ tot] = {x_1 - 1, y_1 - 1, false, 1, ii, 0, time};
				cd[++ tot] = {x_1 - 1, y_2, false, 0, ii, 0, time};
				cd[++ tot] = {x_2, y_1 - 1, false, 0, ii, 0, time};
				break;	
		}
	}
	
	sort(cd + 1, cd + 1 + tot, com1);
	
	solve(1, tot);
	
	for(int i = 1; i <= tot; i ++){
		if(cd[i].pos == 1) continue;
//		if(cd[i].id == 2) cout << cd[i].way << ' ' << cd[i].cnt << endl;
		if(cd[i].way) la_ans[cd[i].id] += cd[i].cnt;
		else la_ans[cd[i].id] -= cd[i].cnt;
	}
	
	for(int i = 1; i <= ii; i ++)
		printf("%lld\n", la_ans[i]);
	return 0;
}

这样，我们在CDQ上的内容就过掉了，下面进入珂朵莉树

Part 2珂朵莉树

--我知道珂朵莉是世界上最幸福的女孩，但珂朵莉树永远是一个暴力数据结构。

先阐述一下珂朵莉树适用于什么情况吧！

数据随机同时有区间推平操作（使一个区间都变成相同的玩意儿）

直接上模板题，对着题目来讲：

Willem, Chtholly and Seniorious

题面翻译

【题面】
请你写一种奇怪的数据结构，支持：

$1$ $l$ $r$ $x$ ：将$[l,r]$ 区间所有数加上$x$
$2$ $l$ $r$ $x$ ：将$[l,r]$ 区间所有数改成$x$
$3$ $l$ $r$ $x$ ：输出将$[l,r]$ 区间从小到大排序后的第$x$ 个数是的多少(即区间第$x$ 小，数字大小相同算多次，保证 $1\leq$ $x$ $\leq$ $r-l+1$ )
$4$ $l$ $r$ $x$ $y$ ：输出$[l,r]$ 区间每个数字的$x$ 次方的和模$y$ 的值(即($\sum^r_{i=l}a_i^x$ ) $\mod y$ )

【输入格式】
这道题目的输入格式比较特殊，需要选手通过$seed$ 自己生成输入数据。
输入一行四个整数$n,m,seed,v_{max}$ （$1\leq $ $n,m\leq 10^{5}$ ,$0\leq seed \leq 10^{9}+7$ $,1\leq vmax \leq 10^{9} $ ）
其中$n$ 表示数列长度，$m$ 表示操作次数，后面两个用于生成输入数据。
数据生成的伪代码如下

其中上面的op指题面中提到的四个操作。

【输出格式】
对于每个操作3和4，输出一行仅一个数。

题目描述

— Willem...

— What's the matter?

— It seems that there's something wrong with Seniorious...

— I'll have a look...

Seniorious is made by linking special talismans in particular order.

After over 500 years, the carillon is now in bad condition, so Willem decides to examine it thoroughly.

Seniorious has $ n $ pieces of talisman. Willem puts them in a line, the $ i $ -th of which is an integer $ a_{i} $ .

In order to maintain it, Willem needs to perform $ m $ operations.

There are four types of operations:

$ 1\ l\ r\ x $ : For each $ i $ such that $ l<=i<=r $ , assign $ a_{i}+x $ to $ a_{i} $ .
$ 2\ l\ r\ x $ : For each $ i $ such that $ l<=i<=r $ , assign $ x $ to $ a_{i} $ .
$ 3\ l\ r\ x $ : Print the $ x $ -th smallest number in the index range $ [l,r] $ , i.e. the element at the $ x $ -th position if all the elements $ a_{i} $ such that $ l<=i<=r $ are taken and sorted into an array of non-decreasing integers. It's guaranteed that $ 1<=x<=r-l+1 $ .
$ 4\ l\ r\ x\ y $ : Print the sum of the $ x $ -th power of $ a_{i} $ such that $ l<=i<=r $ , modulo $ y $ , i.e. .

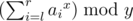输入格式

The only line contains four integers $ n,m,seed,v_{max} $ ( $ 1<=n,m<=10^{{5},0<=seed<10}+7,1<=vmax<=10^{9} $ ).

The initial values and operations are generated using following pseudo code:

def rnd():

    ret = seed
    seed = (seed * 7 + 13) mod 1000000007
    return ret

for i = 1 to n:

    a[i] = (rnd() mod vmax) + 1

for i = 1 to m:

    op = (rnd() mod 4) + 1
    l = (rnd() mod n) + 1
    r = (rnd() mod n) + 1

    if (l > r): 
         swap(l, r)

    if (op == 3):
        x = (rnd() mod (r - l + 1)) + 1
    else:
        x = (rnd() mod vmax) + 1

    if (op == 4):
        y = (rnd() mod vmax) + 1

Here $ op $ is the type of the operation mentioned in the legend.

输出格式

For each operation of types $ 3 $ or $ 4 $ , output a line containing the answer.

样例 #1

样例输入 #1

10 10 7 9

样例输出 #1

样例 #2

样例输入 #2

10 10 9 9

样例输出 #2

提示

In the first example, the initial array is $ {8,9,7,2,3,1,5,6,4,8} $ .

The operations are:

$ 2\ 6\ 7\ 9 $
$ 1\ 3\ 10\ 8 $
$ 4\ 4\ 6\ 2\ 4 $
$ 1\ 4\ 5\ 8 $
$ 2\ 1\ 7\ 1 $
$ 4\ 7\ 9\ 4\ 4 $
$ 1\ 2\ 7\ 9 $
$ 4\ 5\ 8\ 1\ 1 $
$ 2\ 5\ 7\ 5 $
$ 4\ 3\ 10\ 8\ 5 $
————————————————————————————————————————————
珂朵莉树的思想很简单，就是把每一块取出来处理。(下面代码中的变量后面会具体去说)

先讲插入，把这个区间里的整块一个一个取出来，然后删掉，然后塞一块大的进去。

for(It it = s.lower_bound(node(l)); (it -> r) <= r; ){
		int L = it -> l;
		it  ++;
		int R = it -> l - 1;
		s.erase(node(L, R));
	}
s.insert(node(l, r ,x));

二讲区间加法，还是把区间里的整块一个一个找到，然后加上修改的值。

for(It it = s.lower_bound(node(l)); (it -> r) <= r; it ++){
		it -> v += x; //就是因为这里的修改， 导致v要使用muteble 
	}

三讲区间求和，依然是把区间里的整块一个一个找到，然后计算。

for(It it = s.lower_bound(node(l)); (it -> r) <= r; it ++){
		ans += quick_pow(it -> v, mi, p) * (it -> r - it -> l + 1) % p;/*用了一个快速幂*/
		ans %= p;
	}

四讲区间rank，把区间...没错还是把区间里的整块取出存储起来，然后sort, 暴力去做。

	vector <T> vec;
	for(It it = s.lower_bound(node(l)); (it -> r) <= r; it ++)
		vec.push_back({it -> v, it -> r - it -> l + 1});
	sort(vec.begin(), vec.end(), com);
	int i;
	for(i = 0; i < vec.size(); i ++){
		if(vec[i].len < rnk)
			rnk -= vec[i].len;
		else{
			return vec[i].val;
		} 
	}

先什么都别想， it指向的就是一个整块，对应的 $it->l \enspace it->r$就是这个区间的左右端点，$it -> v$就是这一块的数。($[l, r]$里的数全是 $v$)

维护这样的东西好烦啊，但是我们有STL。

使用 set 按照左端点去排序，我们居然会惊奇的发现 set 里面的区间没有重合，且按左端点排号了。

struct node{
	int l, r;
	mutable ll v;//（后面要修改其， 所以mutable）
	node(ll l, ll r = 0, ll v = 0) : l(l), r(r), v(v){}

	friend bool operator < (node x, node y){
		return x.l < y.l;
	}


};

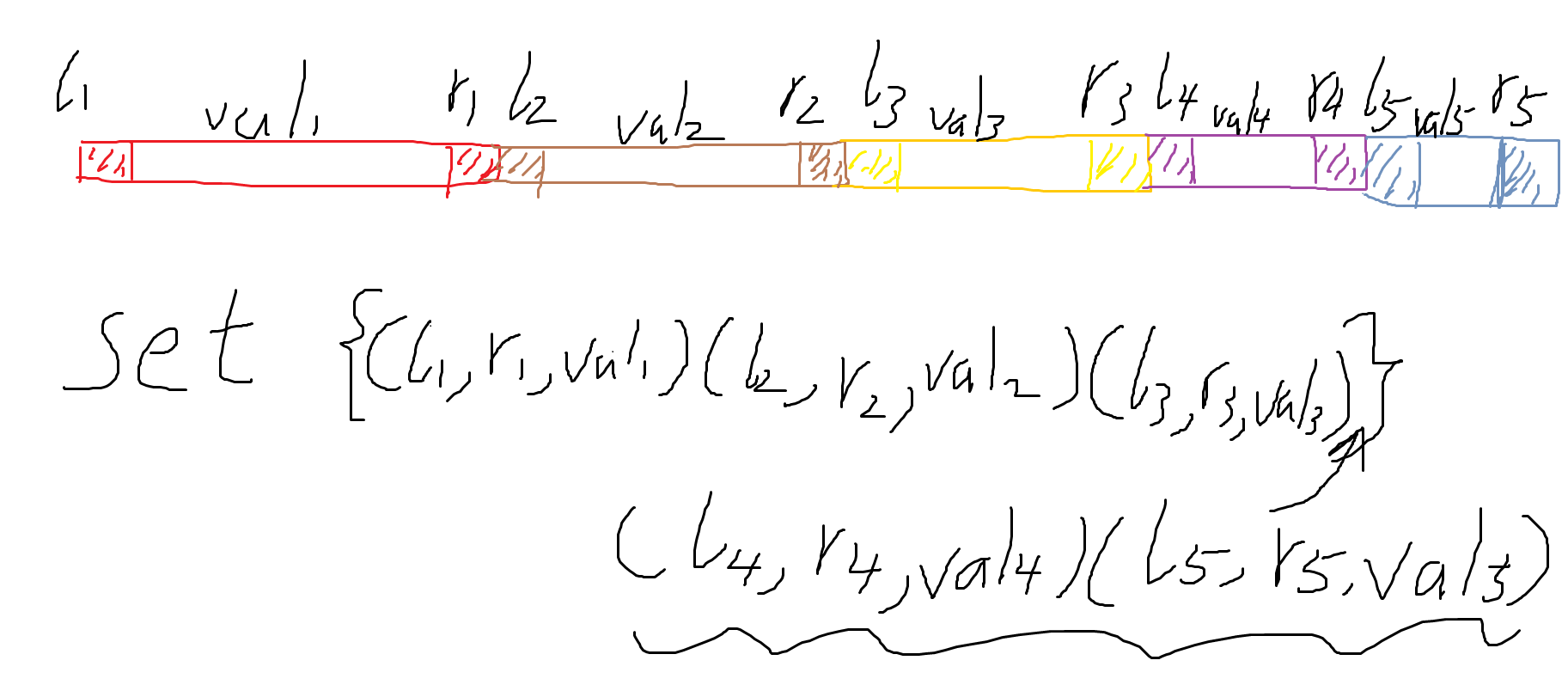
就像这样子。

细心的你一定发现了，有时候操作区间内并不会包含整个部分块，像这样。

肿么办呢？暴力拆开这两个区间...嘿嘿...
这也是这个数据结构的关键部分！

void split(ll pos){//将区间以pos拆开使得 pos为一个区间的开头 
	It it =s.lower_bound(node(pos));
	if(it -> l == pos) return;//已经是了， 直接return
	ll R = (it -> l) - 1;//这一步要参考第一张图， 此时 it->l 是第一个大于pos所在的区间的左端点， 那么将他 -1 不正是 pos所在区间的右端点吗 (在assign中也用到了这一性质)
	it --;//向前推一个 
	
	ll L = (it -> l);
	ll pv = it -> v; //提取出当前区间的玩意儿
	
	s.erase(it); //那么就拆开当前区间了
	s.insert(node(L, pos - 1, pv));
	s.insert(node(pos, R, pv)); 
}

可能你还要问，如果pos在最后一个块中怎么办，指针不会漂移么？
没事，在主函数多搞一个

s.insert(node(n + 1, 1145, 190307));//这里的l一定要是 n + 1, r要是一个极大值， 结合上面的split

保险一点，在搞一个兜底

s.insert(node(0, 0, 0));

上代码！

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define It set <node> :: iterator
const ll Mod = 1e9 + 7;
const ll N = 1e5 + 1134;
ll n, m, seed, vmax;
ll a[N];
ll rnd(){
	ll ret = seed;
	seed = (seed * 7 + 13) % Mod;
	return ret;
}
ll op, l, r, x, y;

struct node{
	int l, r;
	mutable ll v;
	node(ll l, ll r = 0, ll v = 0) : l(l), r(r), v(v){}

	friend bool operator < (node x, node y){
		return x.l < y.l;
	}
	
};

set<node> s;

void split(ll pos){//返回的是以pos为开头的区间的迭代器 
	It it =s.lower_bound(node(pos));
	if(it -> l == pos) return;//找到力！
	ll R = (it -> l) - 1;
	it --;//向前推一个 
	
	//从这里往上的三行本质上就是去查找pos这个点  pps 超过了当前区间的右端点， 又因为这几个区间是没有重合部分的， 不存在 【（）】的情况， 所以直接取最后一个 
	ll L = (it -> l);
	ll pv = it -> v; //提取出当前区间的玩意儿
	
	s.erase(it); //那么就拆开当前区间了
	
	s.insert(node(L, pos - 1, pv));
	s.insert(node(pos, R, pv)); 
}

void assign (ll l, ll r, ll x){
	split(r + 1),split(l);
	for(It it = s.lower_bound(node(l)); (it -> r) <= r; ){
		int L = it -> l;
		it  ++;
		int R = it -> l - 1;
		s.erase(node(L, R));
	}
	s.insert(node(l, r ,x));
} 

void Add(ll l, ll r, ll x){
	split(r + 1), split(l);
	for(It it = s.lower_bound(node(l)); (it -> r) <= r; it ++){
		it -> v += x; 
//
就是因为这里的修改， 导致v要使用muteble 
	}
} 

struct T{
	ll val, len;
};

bool com(T a, T b){
	return a.val < b.val;
}

ll get_val(ll l, ll r, ll rnk){
	split(r + 1), split(l);
	vector <T> vec;
	for(It it = s.lower_bound(node(l)); (it -> r) <= r; it ++)
		vec.push_back({it -> v, it -> r - it -> l + 1});
	sort(vec.begin(), vec.end(), com);
	int i;
	for(i = 0; i < vec.size(); i ++){
		if(vec[i].len < rnk)
			rnk -= vec[i].len;
		else{
			return vec[i].val;
		} 
	}
	
	return vec[vec.size() - 1].val;
}

ll quick_pow(ll a, ll b, ll p){
	if(b == 0) return 1;
	if(b & 1) return a % p * quick_pow(a, b - 1, p) % p;
	ll cun = quick_pow(a, b / 2, p) % p;
	return cun * cun % p; 
}

ll get_mi(ll l, ll r, ll mi, ll p){
	split(r + 1), split(l);
	ll ans = 0;
	for(It it = s.lower_bound(node(l)); (it -> r) <= r; it ++){
		ans += quick_pow(it -> v, mi, p) * (it -> r - it -> l + 1) % p;
		ans %= p;
	}
	
	return ans;
}
int main(){
	scanf("%lld%lld%lld%lld", &n, &m, &seed, &vmax);
	s.insert(node(0, 0, 9090));
	s.insert(node(n + 1, 200000, 200000));//这里的l一定要是 n + 1, r要是一个极大值 
	for(int i = 1; i <= n; i ++)
		a[i] = (rnd() % vmax) + 1, s.insert(node(i, i, a[i]));

	while(m --){
		op = (rnd() % 4) + 1;
		l = (rnd() % n) + 1;
		r = (rnd() % n) + 1;
		if(l > r) swap(l, r);
		if(op == 3)
			x = (rnd() % (r - l + 1)) + 1;
		else
			x = (rnd() % vmax) + 1;
			
		if(op == 4)
			y = (rnd() % vmax) + 1;
//		cout << op <<' '<<l <<' ' << r<< endl;
		switch(op){
			case 1:
				Add(l, r, x);
				break;
			case 2:
				assign(l, r, x);
				break;
			case 3:
				printf("%lld\n", get_val(l, r, x));
				break;
			case 4:
				printf("%lld\n",  get_mi(l, r, x, y));
				break;
		}
	}
	return 0;
}

Part 3 最终章

这道题中包含着区间修改以及区间查询，发现有区间推平，想到珂朵莉树。

但是具体怎么操作却还是一头雾水。

那么从最简单的无修改区间数颜色开始吧。

[SDOI2009] HH的项链

题目描述

HH 有一串由各种漂亮的贝壳组成的项链。HH 相信不同的贝壳会带来好运，所以每次散步完后，他都会随意取出一段贝壳，思考它们所表达的含义。HH 不断地收集新的贝壳，因此，他的项链变得越来越长。

有一天，他突然提出了一个问题：某一段贝壳中，包含了多少种不同的贝壳？这个问题很难回答…… 因为项链实在是太长了。于是，他只好求助睿智的你，来解决这个问题。

输入格式

一行一个正整数 $n$，表示项链长度。
第二行 $n$ 个正整数 $a_i$，表示项链中第 $i$ 个贝壳的种类。

第三行一个整数 $m$，表示 HH 询问的个数。
接下来 $m$ 行，每行两个整数 $l,r$，表示询问的区间。

输出格式

输出 $m$ 行，每行一个整数，依次表示询问对应的答案。

样例 #1

样例输入 #1

6
1 2 3 4 3 5
3
1 2
3 5
2 6

样例输出 #1

2
2
4

提示

【数据范围】

对于 $20\%$ 的数据，$1\le n,m\leq 5000$；
对于 $40\%$ 的数据，$1\le n,m\leq 10^5$；
对于 $60\%$ 的数据，$1\le n,m\leq 5\times 10^5$；
对于 $100\%$ 的数据，$1\le n,m,a_i \leq 10^6$，$1\le l \le r \le n$。

本题可能需要较快的读入方式，最大数据点读入数据约 20MB
————————————————————————————————————————————
在处理区间数色问题时，有一个较为套路的做法。

对于每一个位置 $i$ 记录前一个与其颜色($val_i$)相同的位置 $pre_i$,没有的话就等于 $0$

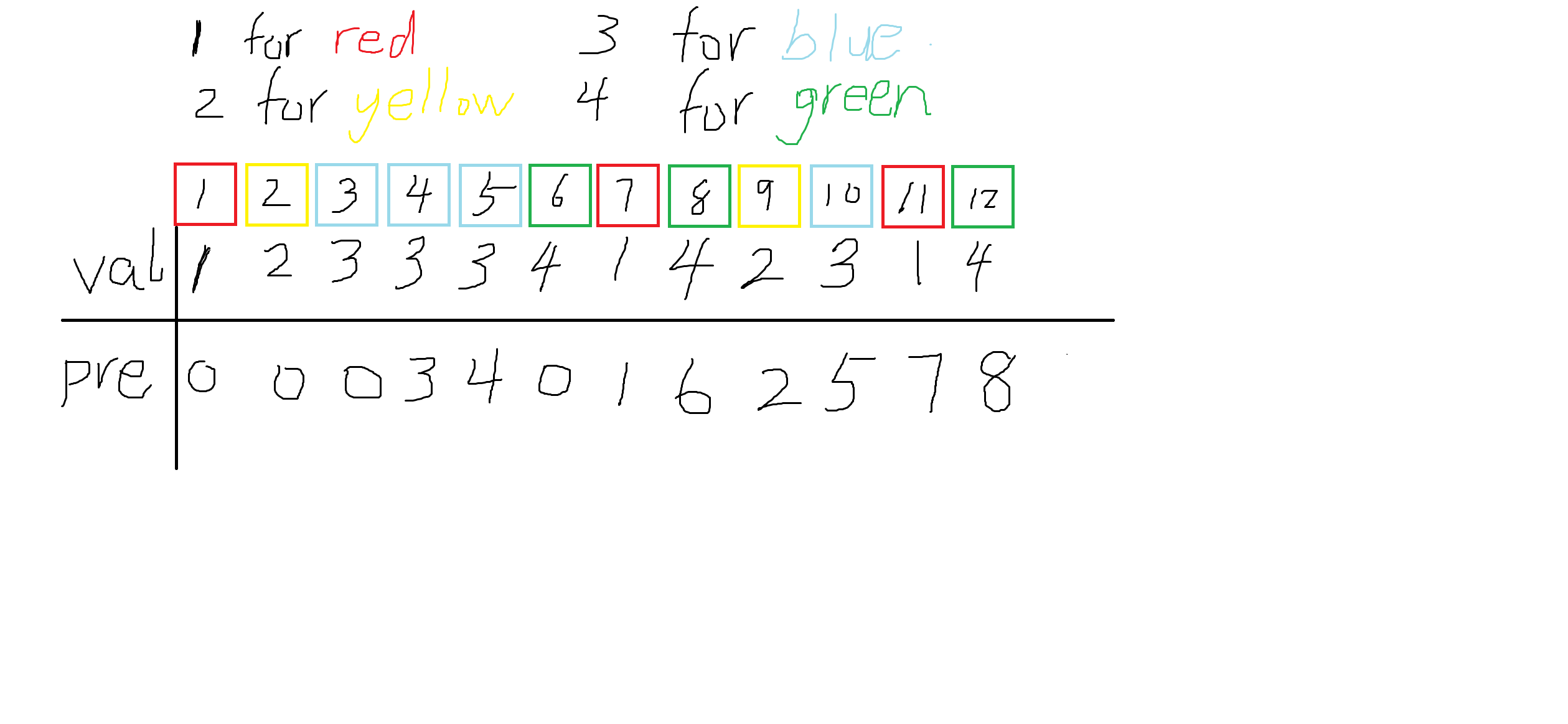
然后有个结论性的玩意儿。

设位置 $i$ 若 $pre_i < l \enspace $, 那么 $i$ 对区间 $[l, r]$有贡献, 否则没有。

有点抽象，给一张图感性理解一下罢！

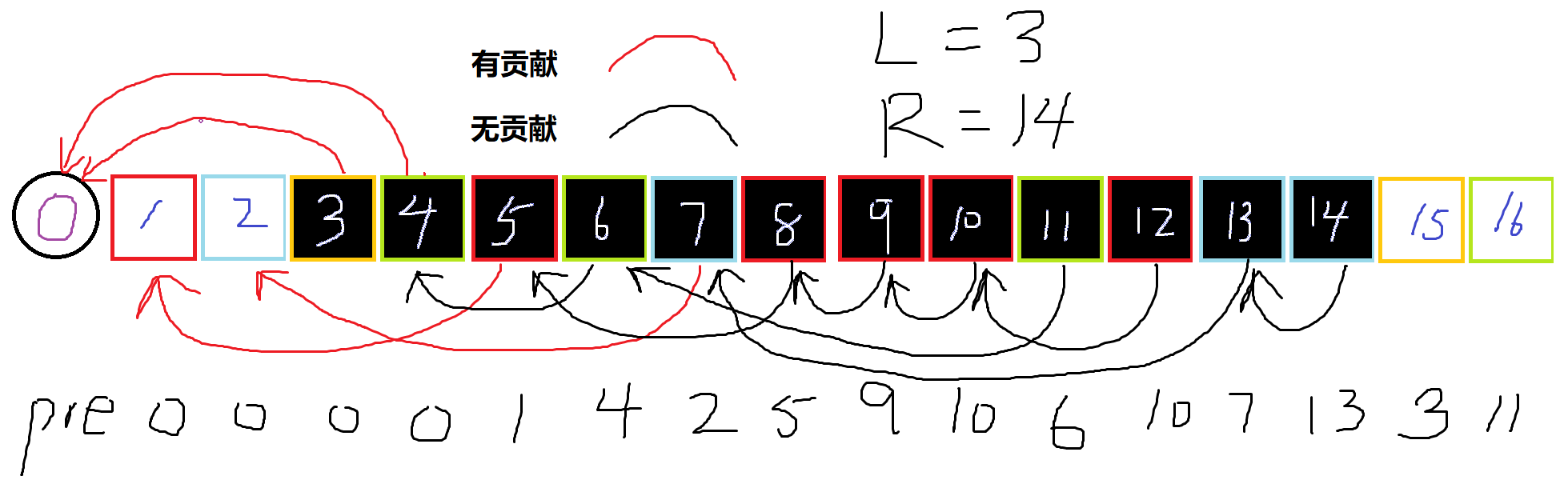
其中箭头指向的是pre数组的下表，会发现如果指向的玩意儿在区间内，那么它的贡献已经被它指向的玩意儿算过了。

所以我们要满足

\[pre_i < l \]

即

\[pre_i \le l - 1 \]

才有贡献。
同时$i$ 要在区间范围内。也就是说

\[l \le i \le r \]

两个一结合：

\[pre_i \le l -1 \]

\[l \le i \le r \]

还看不出来？那么这样呢？

\[0 \le pre_i \le l - 1 \]

\[l \le i \le r \]

没错，正是静态二维数点的形式，现在都没有了时间的约束，应该很好做罢！
事实上，对于每一个

\[i \]

我们可以看成点

\[(i, pre_i) \]

而每一次的查询可以看成是矩形内点的个数，这里只是一个小例子

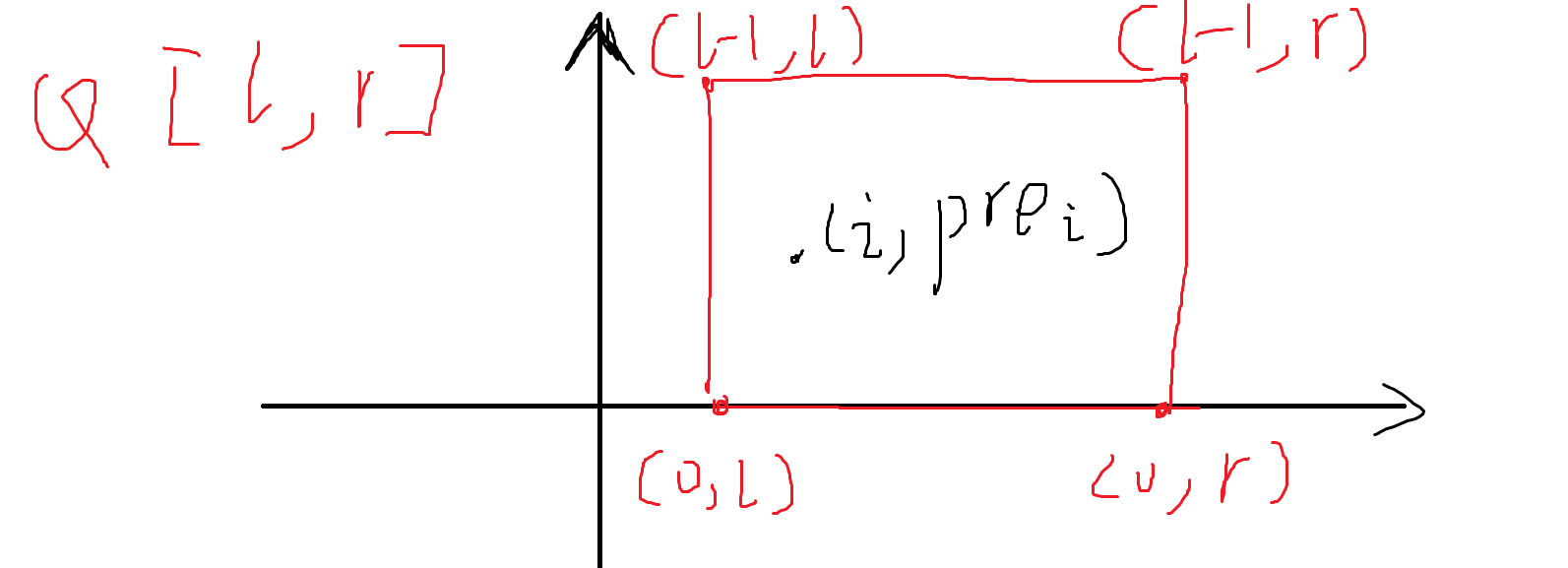
处理细节的一些小技巧：

但是注意到树状数组可能会存到 $0$ 上，因为。

\[0 \le pre_i \le l \]

稍作变形

\[1 \le pre_i + 1 \le l + 1 \]

一些细节处稍微注意一下就好，上代码：

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 114;
int n, m;
int a[N];
int pre[N], now[N];
int tr[N];
struct T{
	int id, v, way, limi;
}cd[N * 2];

bool com(T a, T b){
	return a.v < b.v;
}

int lb(int x){
	return x & (-x);
}

void Add(int pos, int val){
	while(pos <= n){
		tr[pos] += val;
		pos += lb(pos);
	}
}

int Que(int pos){
	int ans = 0;
	while(pos){
		ans += tr[pos];
		pos -= lb(pos);
	}
	return ans;
}
int l_ans[N];
int main(){
	scanf("%d",  &n);
	for(int i = 1; i <= n; i++){
		scanf("%d", &a[i]);
		pre[i] = now[a[i]] + 1;
		now[a[i]] = i;
	}
	int tot = 0;
	scanf("%d", &m);
	for(int i = 1; i <= m; i ++){
		int l, r;
		scanf("%d%d", &l, &r);
		cd [++ tot] = {i, l - 1, -1, l};
		cd [++ tot] = {i, r, 1, l};
	}
	sort(cd + 1, cd + tot + 1, com);
	int r = 1;
	for(int i = 1; i <= tot; i ++){
		int L = cd[i].v;
		while (r <= L) Add(pre[r], 1), r ++;
		l_ans[cd[i].id] += cd[i].way * Que(cd[i].limi);
	}
	
	for(int i = 1; i <= m; i ++)
		cout << l_ans[i]<< endl;
	return 0;
}

这是静态无修改的，那么带修改的呢，我们从单点开始。

[国家集训队] 数颜色 / 维护队列

题目描述

墨墨购买了一套 $N$ 支彩色画笔（其中有些颜色可能相同），摆成一排，你需要回答墨墨的提问。墨墨会向你发布如下指令：

$Q\ L\ R$ 代表询问你从第 $L$ 支画笔到第 $R$ 支画笔中共有几种不同颜色的画笔。
$R\ P\ Col$ 把第 $P$ 支画笔替换为颜色 $Col$。

为了满足墨墨的要求，你知道你需要干什么了吗？

输入格式

第 $1$ 行两个整数 $N$，$M$，分别代表初始画笔的数量以及墨墨会做的事情的个数。

第 $2$ 行 $N$ 个整数，分别代表初始画笔排中第 $i$ 支画笔的颜色。

第 $3$ 行到第 $2+M$ 行，每行分别代表墨墨会做的一件事情，格式见题干部分。

输出格式

对于每一个 Query 的询问，你需要在对应的行中给出一个数字，代表第 $L$ 支画笔到第 $R$ 支画笔中共有几种不同颜色的画笔。

样例 #1

样例输入 #1

6 5
1 2 3 4 5 5
Q 1 4
Q 2 6
R 1 2
Q 1 4
Q 2 6

样例输出 #1

提示

对于30%的数据，$n,m \leq 10000$

对于60%的数据，$n,m \leq 50000$

对于所有数据，$n,m \leq 133333$

所有的输入数据中出现的所有整数均大于等于 $1$ 且不超过 $10^6$。

本题可能轻微卡常数

来源：bzoj2120

本题数据为洛谷自造数据，使用 CYaRon 耗时5分钟完成数据制作。

————————————————————————————————————————————
本题虽然使用莫队就可以硬C过去（人家算法标签里也只有莫队），但是却是一道不错的CDQ分治的练手题。

看到有修改，直接多开一维时间。

修改的过程中一定是对某些玩意儿的贡献消失了，同时增加对某些玩意儿的贡献。

也就是说我们可以通过删某个点（减掉该点的贡献），再通过增加某个点（增加这个点的贡献）来完成修改操作，下面给出了一个图就可以看出来辣：

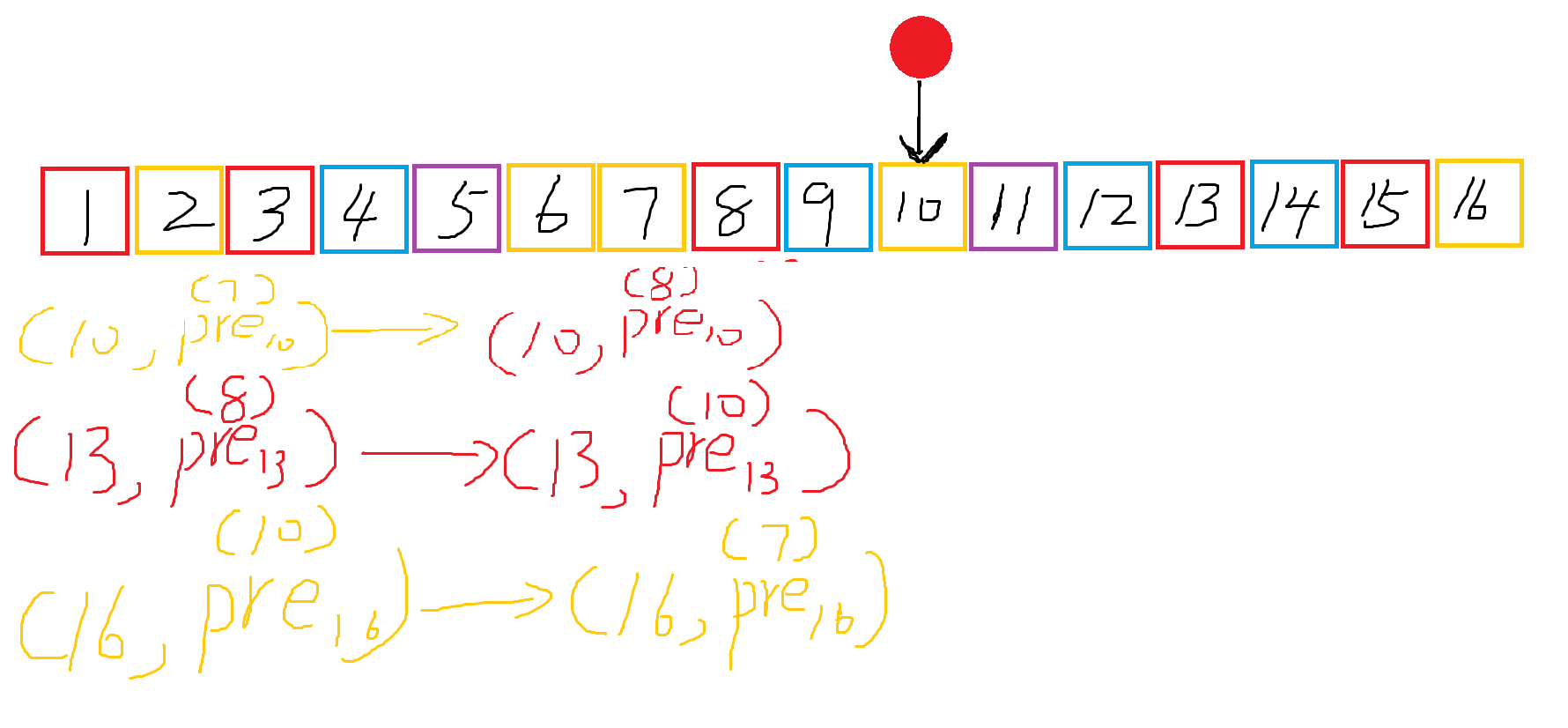
这揭示了哪些点被删，和哪些点被加。

也解释了 $pre$ 的变化。

可能产生变化的只有以下几个点（以及 $pre$的修改变化）

\[修改前颜色的后一个与其同色的节点(如果有的话) -- pre 变为当前节点的 pre \]

\[当前节点 -- pre 变为修改后颜色的后继的 pre（有后继的话，否则为0） \]

\[修改后颜色的后一个与其同色的节点(如果有的话) -- pre 变为当前节点 \]

那么修改的顺序也稍有讲究（小细节辣）。

那么如何迅速找到这些玩意儿呢？

对于每一个颜色建立一个set（本题颜色不多，不要离散化）
按照出现位置排序。然后利用其中的成员函数就可以不费吹灰之力找到辣。

包括初始的几个颜色，也可以视作插入操作。

struct T{
	bool op;//[op : 1修改/ 0查询]
	int pos;//查询的位置 --> 第二关键字 
	int val;//[“第三关键字 ”]  "存的时候还没有 + 1"
	int time;//第一关键字
	int id; //映射到答案的编号
	int way;//[修改：+ or -//查询：对答案 + or -] 
} cd[N * 3];

void sep(int pos, int val){ //将一个修改进行分开 
	if(a[pos] == 0){ //初始的几个点直接特判（这里是按从前到后的顺序插入的， 详情可见完整代码）
		s[val].insert(pos);//s为set 这里是在颜色为val的集合里插入 pos
		It it = s[val].lower_bound(pos);//这时 *it == pos
		it --;//左移一下， 刚好是pos的前驱
//因为按顺序， 所以他不会有后继有影响， 只对当前节点有影响
		pre[pos] = *it;//维护一下pre数组
		cd[++ cnt] = {1, pos, pre[pos], tim, 0, 1};//记录下操作
		a[pos] = val;//维护颜色
	}else{
		int pcol = a[pos];//之前的颜色
		if(pcol == val) return; //同色不要操作 
		It itr = s[pcol].lower_bound(pos);//指针之前颜色的位置
		itr ++;//向后移一个， 那么就是之前颜色的后继
		int p = *itr;//指向那个位置
		if(p != N){ //存在后继
			cd[++ cnt] = {1, p, pre[p], tim, 0, -1}; //当前后继的前驱要先删 
			cd[++ cnt] = {1, p, pre[pos], tim, 0, 1};//当前后继的前驱要重加 （这边要满足存在后继！）
			pre[p] = pre[pos];//维护一下pre
		} //跟上面写的一样
		itr --;//回到原来的位置
		s[pcol].erase(itr);//删除原来的 
		s[val].insert(pos);//加入新来的 
		cd[++ cnt] = {1, pos, pre[pos], tim, 0, -1};//当前前驱要先删 
		itr = s[val].lower_bound(pos);//指向当前位置（val）
		itr ++;//找到后继
		p = *itr;//指一下
		if(p != N){//存在后继
			cd[++ cnt] = {1, p, pre[p], tim, 0, -1}; //前驱删掉 
			cd[++ cnt] = {1, p, pos, tim, 0, 1};//前驱改为当前的位置
			pre[p] = pos;//维护pre
		} 
		itr --;
		itr --;//指到前驱
		cd[++ cnt] = {1, pos, *itr, tim, 0, 1}; //修改一下pos的前驱 
		pre[pos] = *itr;//维护pre
		a[pos] = val;//维护颜色
	}
}

这是所有的修改操作，也就是比较难理解的部分。

下面给出完整代码（看了上面的玩意儿应该会很好理解吧？）

#include <bits/stdc++.h>
using namespace std;
//在这道题里面似乎可以直接去搞颜色块， 没有必要去维护整个玩意儿
const int N = 1e5 + 114514;
const int M = 1e6 + 112;
#define It set <int> :: iterator
struct T{
	bool op;//[op : 1修改/ 0查询]
	int pos;//查询的位置 --> 第二关键字 
	int val;//[“第三关键字 ”] 
	int time;//第一关键字
	int id; //映射到答案的编号
	int way;//[修改：+ or -//查询：对答案 + or -] 
} cd[N * 3];
set <int> s[M];
int tr[M];
int n, m;
int cnt = 0, tim = 1, Id; //始终记住我们要维护pre 
int a[N] = {0};
int pre[N], tmp;
int l_ans[N];
bool com1 (T a, T b){
	if(a.time == b.time){
		return a.pos < b.pos;
	}
	return a.time < b.time;
}

bool com2 (T a, T b){
	return a.pos < b.pos;
} 

int lb(int x){
	return x & (-x);
}

void Add(int x, int val){
	while (x <= n){
		tr[x] += val;
		x += lb(x);
	}
}

int Que(int x){
	int ans = 0;
	while(x){
		ans += tr[x];
		x -= lb(x);
	}
	return ans;
}


void sep(int pos, int val){ //将一个修改进行分开 
//	cout << pos << ' ' << val << endl;
	if(a[pos] == 0){ //直接插入就可以 
		s[val].insert(pos);
		It it = s[val].lower_bound(pos);
		//不可能有后继！
		it --;
		pre[pos] = *it;
		cd[++ cnt] = {1, pos, pre[pos], tim, 0, 1};
		a[pos] = val;
		//第一次插入只对当前的前驱有影响！ 
	}else{
		int pcol = a[pos];
		if(pcol == val) return; //同色不要操作 
		It itr = s[pcol].lower_bound(pos);
		itr ++;
		int p = *itr;
		if(p != N){ //存在后继
			cd[++ cnt] = {1, p, pre[p], tim, 0, -1}; //当前后继的前驱要先删 
			cd[++ cnt] = {1, p, pre[pos], tim, 0, 1};//当前后继的前驱要重加 （这边要满足存在后继！）
			pre[p] = pre[pos];
		} 
		itr --;
		s[pcol].erase(itr);//删除原来的 
		s[val].insert(pos);//加入新来的 
		cd[++ cnt] = {1, pos, pre[pos], tim, 0, -1};//当前前驱要先删 
		itr = s[val].lower_bound(pos);
		itr ++;
		p = *itr;
		if(p != N){
			cd[++ cnt] = {1, p, pre[p], tim, 0, -1}; //前驱删掉 
			cd[++ cnt] = {1, p, pos, tim, 0, 1};//前驱改为当前的位置 
			pre[p] = pos;
		} 
		itr --;
		itr --;
		cd[++ cnt] = {1, pos, *itr, tim, 0, 1}; //修改一下pos的前驱 
		pre[pos] = *itr;
		a[pos] = val;
	}
}

void sep_Q(int l, int r){
	cd[++ cnt] = {0, r, l - 1, tim, Id, 1};
	cd[++ cnt] = {0, l - 1, l - 1, tim, Id, -1}; 
} 


void cdq(int l, int r){
	if(l == r) return ;
	int mid = (l + r) >> 1;
	cdq(l, mid), cdq(mid + 1, r);
	sort(cd + l, cd + mid + 1, com2);
	sort(cd + mid + 1, cd + r + 1, com2);
	int L = l, R = mid + 1;
	for(; R <= r; R ++){
		if(cd[R].op == 1) continue;//这...不要啦...不要修改啦...不要..呜呜 
		while(L <= mid && cd[L].pos <= cd[R].pos){
			if(cd[L].op == 0) {L ++; continue;} //不要...呜呜..不要..不要查询 >w<
			Add(cd[L].val + 1, cd[L].way);
			L ++;
		}
		l_ans[cd[R].id] += (cd[R].way * Que(cd[R].val + 1));
	}
	for(int i = l; i < L; i ++){
		if(cd[i].op == 0) continue; //哼，前面不让我插（入）树状数组， 别想让我再 插（出来）
		Add(cd[i].val + 1, - cd[i].way); 
	}
	return ;
}
int main(){
	for(int i = 1; i <= M - 112; i ++)
		s[i].insert(0), s[i].insert(N); //分别是这颜色的第一个和最后一个 
	scanf("%d%d", &n, &m);
	for(int i = 1; i <= n; i ++)
		scanf("%d", &tmp), sep(i, tmp);
	for(int i = 1; i <= m; i ++){
		char op;
		int l, r;
		tim ++; 
		cin >> op;
		scanf("%d%d", &l, &r);
		if(op == 'R'){
			if(l > n) continue;
			sep(l, r);
		}
		else {
			++ Id, sep_Q(l, min(r, n));
		}
	}
	
	sort(cd + 1, cd + 1 + cnt, com1);
	
	cdq(1, cnt);
	
	for(int i = 1; i <= Id; i ++)
		printf("%d\n", l_ans[i]);
	return 0;
}

镜中的昆虫题解也来不及写了，就把代码贴上罢，也算是一个交代了
（退役一年之后）

#include <bits/stdc++.h>
using namespace std;
#define It set<Pa> :: iterator
const int N = 1e5 + 114005;
int n, m, Id = 0;
int a[N], b[N * 2], cnt = 0;
map <int, int> mp;
int id_col[N * 2];
struct Pa{
	int l, r;
	Pa (int l, int r = 0) : l(l), r(r) {}
	bool operator < (const Pa &x) const {
		return l < x.l;
	}
};
struct T{
	int op, l, r, x; //存储一下操作， 准备离线操作
}tmp[N];

struct F{
	int op;//[op : 1 查询/ 0 修改]
	int tim;//[tim : 第一关键字]
	int pos;//[pos : 位置， 第二关键字]
	int pr; //[pre : 第三关键字]
	int id;//对应到最后答案的id
	int way;//造成贡献的形式 - or +
}cd[N * 20];

bool com1(F a, F b){
	if(a.tim == b.tim){
		if(a.pos == b.pos)
			return a.pr < b.pr;
		return a.pos < b.pos;
	}
	return a.tim < b.tim;
}

bool com2(F a, F b){
	return a.pos < b.pos;
}
int l_ans[N]; //最后的答案
int pre[N]; //维护一下pre, 以及 a
int tot = 0;
struct CC{
	set<Pa> col;//左端点 和 颜色
	set<Pa> s[N];//左端点和右端点
	
	inline void Spl (int pos){ //将pos作为一个区间的开头分裂
		It it = col.lower_bound(Pa(pos));
		if(it -> l == pos) return;
		int R = (it -> l) - 1;
		it --;
		int c = it -> r;
		int L = it -> l;
		/*if(pos == L) return; ******/
		col.erase(it);col.insert(Pa(L, c));col.insert(Pa(pos, c));
		s[c].erase(Pa(L, R));s[c].insert(Pa(L, pos - 1));s[c].insert(Pa(pos, R));
//		It it = col.lower_bound(Pa(pos + 1));
//		int  R = it  -> l - 1;-- it;
//		int L = it -> l;
//		if(pos == R) return ;
//		int c = it->r;
//		col.erase(it);
//		col.insert(Pa(L, c));
//		col.insert(Pa(pos + 1, c));
//		s[c].erase(Pa(L, R));
//		s[c].insert(Pa(L, pos));
//		s[c].insert(Pa(pos + 1, R));
	}
	
	void Insert(int l, int r, int c, int t){
		Spl(l);Spl(r + 1);//直接搞出来 l ~ r 这部分一定是一块一块的
		for(It it = col.lower_bound(Pa(l)); (it->l) <= r;){
			int L = it -> l, Col = it -> r;
			it ++;
			int R = it -> l - 1;
			col.erase(Pa(L, Col));
			s[Col].erase(Pa(L, R));
			if(L == l){ //特判一下
				int e = (--(s[c].lower_bound(Pa(L)))) -> r;
				if(pre[L] != e){//要修改哦
					cd[++ tot] = {0, t, L, pre[L], 0, -1};
					pre[L] = e;
					cd[++ tot] = {0, t, L, pre[L], 0, 1};
				}
			}else{
				if(pre[L] != L - 1){
					cd[++ tot] = {0, t, L, pre[L], 0, -1};
					pre[L] = L - 1;
					cd[++ tot] = {0, t, L, pre[L], 0, 1};
				}
			}
			L = R + 1;
			R = (s[Col].lower_bound(Pa(L))) -> l;//这个是修改前后面一段的前面
			int e = (-- s[Col].lower_bound(Pa(l))) -> r;//这里对应修改前的一段的后面
			if(R <= n && r < R && pre[R] != e){
				cd[++ tot] = {0, t, R, pre[R], 0, -1};
				pre[R] = e;
				cd[++ tot] = {0, t, R, pre[R], 0, 1};
			}
		}
		if(r + 1 <= n){
		It it = s[c].lower_bound(Pa(r + 1)); //找到后面一段颜色为c的
		int L = it -> l;
		if(pre[L] != r && L <= n){//放止他是最后一个， 指到了兜底的极大值
			cd[++ tot] = {0, t, L, pre[L], 0, -1};
			pre[L] = r;
			cd[++ tot] = {0, t, L, pre[L], 0, 1};
		}}
		s[c].insert(Pa(l, r));
		col.insert(Pa(l, c));
		int L = r + 1; //后面一个点我们是没有维护的
		if(L <= n){ //存在
			It it = col.lower_bound(L);
			int Col = it -> r;
			int e = (-- s[Col].lower_bound(Pa(L))) -> r;
			if(pre[L] != e){
				cd[++ tot] = {0, t, L, pre[L], 0, -1};
				pre[L] = e;
				cd[++ tot] = {0, t, L, pre[L], 0, 1};
			}
		}
	}
}co;

struct TR{
	int tr[N + 112];
	int lb(int x){
		return x & (-x);
	}
	
	void Add(int pos, int val){
		while(pos <= N){
			tr[pos] += val;
			pos += lb(pos);
		}
	}
	
	int Que(int pos){
		int ans = 0;
		while(pos){
			ans += tr[pos];
			pos -= lb(pos);
		}
		return ans;
	}
}Tr;

void cdq(int l, int r){
	if(l == r) return ;
	int mid = (l + r) >> 1;
    cdq(l, mid);cdq(mid + 1, r);
	sort(cd + l, cd + mid + 1, com2);
	sort(cd + mid + 1, cd + r + 1, com2);
	
	int L = l, R = mid + 1;
	for(; R <= r; R ++){
		if(cd[R].op == 0) continue;//唔...呃啊..不..不要修改...呜呜
		while(L <= mid && cd[L].pos <= cd[R].pos){
			if(cd[L].op == 1) {L ++;continue;}//不要...呼呼..不..唔...不要..呜啊..查询...
			Tr.Add(cd[L].pr + 1, cd[L].way);//这边插进去！舒服！ >w< 
//			cout << cd[L].way << endl;
			L ++;
		}
		l_ans[cd[R].id] += Tr.Que(cd[R].pr + 1)* cd[R].way;
	}
	for(int i = l; i < L; i ++){
		if(cd[i].op == 1) continue;
		Tr.Add(cd[i].pr + 1, -cd[i].way);
	}	 
	return ;
}
int main(){
	scanf("%d%d", &n, &m);
	for(int i = 1; i <= n; i ++){
		scanf("%d", &a[i]);
		b[++ tot] = a[i];
	}
	
	for(int i = 1; i <= m; i ++){
		scanf("%d%d%d", &tmp[i].op, &tmp[i].l, &tmp[i].r);
		if(tmp[i].op == 1) scanf("%d", &tmp[i].x), b[++ tot] = tmp[i].x;	
	}
	
	sort(b + 1, b + 1 + tot);
	mp [b[1]] = ++ cnt;
	
	for(int i = 2; i <= tot; i ++)
		if(b[i] != b[i - 1]) mp[b[i]] = ++ cnt; //离散化
		
	for(int i = 1; i <= cnt; i ++)
		co.s[i].insert(Pa(0, 0));
//		cout << "p" << endl;
	tot = 0;
//把a数组处理一下， 顺便把pre先维护好
	for(int i = 1; i <= n; i ++){
		a[i] = mp[a[i]];
		pre[i] = (--co.s[a[i]].end()) -> r;
		cd[++ tot] = {0, 0, i, pre[i], 0, 1};
		co.s[a[i]].insert(Pa(i, i));
		co.col.insert(Pa(i, a[i]));
	}
	
 	for(int i = 1; i <= cnt; i ++)
 		co.s[i].insert(Pa(n + 1, 0)); //插一个兜底
 
 	co.col.insert(Pa(0, 0));
 	co.col.insert(Pa(n + 100, n + 1));
 	
 	for(int i = 1; i <= m; i ++){
		if(tmp[i].op == 1) 	
			co.Insert(tmp[i].l, tmp[i].r, mp[tmp[i].x], i);
		else{
			Id ++;
			cd[++ tot] = {1, i, tmp[i].r, tmp[i].l - 1, Id, 1};
			cd[++ tot] = {1, i, tmp[i].l - 1, tmp[i].l - 1, Id, -1};
		}
	}
////	for(int i = 1; i <= tot; i ++){
////		cout << cd[i].op << ' ' << cd[i].pos <<' ' << cd[i].pr <<' '<< cd[i].way << endl;
////	}
	sort(cd + 1, cd + 1 + tot, com1);
	cdq(1, tot);
	
	for(int i = 1; i <= Id; i ++)
		printf("%d\n", l_ans[i]);
	return 0;
}

posted @ 2022-11-11 21:26 ska_0x08 阅读(82) 评论(0) 收藏举报

刷新页面返回顶部

命令	参数	意义
\(0\)	\(w\)	初始化一个全零矩阵。本命令仅开始时出现一次。
\(1\)	\(x\,y\,a\)	向方格 \((x,y)\) 中添加 \(a\) 个用户。\(a\) 是正整数。
\(2\)	\(x1\,y1\,x2\,y2\)	查询 \(x1\leq x\leq x2\)，\(y1\leq y\leq y2\) 所规定的矩形中的用户数量。
\(3\)	无参数	结束程序。本命令仅结束时出现一次。

Ska_0x08's Blog

CDQ && 珂朵莉树

Part 1 CDQ分治

【模板】三维偏序（陌上花开）

题目背景

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

提示

[CQOI2011]动态逆序对

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

提示

[BOI2007]Mokia 摩基亚

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

提示

数据规模与约定

Part 2珂朵莉树

Willem, Chtholly and Seniorious

题面翻译

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

样例 #2

样例输入 #2

样例输出 #2

提示

Part 3 最终章

[SDOI2009] HH的项链

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

提示

[国家集训队] 数颜色 / 维护队列

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

提示

公告