省常中游记

Day 1

没有题解 全是数论 T1 类欧几里得 T2 积函数 T3 容斥原理 T4 仙人掌拆分

Day 2

上午纯坐牢

T1

题目描述

盒子里有 \(n\) 个球，球的颜色有黑白两种，但是不知道初始状态

一共进行 \(m\) 操作，每次会从盒子中取出一个球，然后放入黑白各一个球，然后再取出一个球

取出的 \(2m\)个球会形成一个序列，你需要对所有初始状态计算本质不同的序列对
\(p\) 取模的结果

两个序列不同当且仅当存在一个位置，其所代表的球的颜色在两个序列中不同

这里的初始状态指的是盒子中两种颜色的球的个数

输入格式

一行三个数 \(n, m, p\)

输出格式

一行一个数表示答案

样例输入

 1 2 114514

样例输出

 8

数据范围

$ 1 \le n, m \le 3 * 10^{3}, 1 \le p \le 10^{9}$

题解

Code

T2

题目描述

定义一个可重集 \(S\) 的众数 \(f(S)\) 为集合中出现次数最多且编号最小的数字。例如 \(f(1,2,2,3) = 2,f(2,2,3,3) = 2\)。

定义一个可重集 \(S\) 的价值为\(2^{f(S)}\) 。

现在你有一个长度为 \(n\) 的序列 \(a_{1},a_{2},...,a_{n}\)，其中数字 \(a_{x}\) 表示可重集 \(S\) 中正整数 \(x\) 出现了 \(a_{x}\) 次。你需要将这个可重集 \(S\) 不重、不漏地划分成若干个可重集，使得这些可重集的价值之和最小。

你只需要输出这个数值在模 \(998244353\) 意义下的结果。

接下来，会有 \(q\) 次修改，每次修改会将 \(a_{x}\) 改为 \(y\) 。每次修改后你都要重新输出上面所描述的数值。

输入格式

第一行一个正整数 \(n\) ，表示序列的长度。

接下来一行 \(n\) 个正整数，分别表示$a_{1}, a_{2}, ..., a_{n} $。

接下来一个正整数 \(q\) ，表示修改次数。

接下来 \(q\) 行，每行两个正整数 \(x, y\)，表示将 \(a_{x}\) 改为 \(y\)。

输出格式

答案对 \(9982444353\) 取模。

在修改之前，先输出一个数值表示答案。

每次修改之后，都要输出一个数值表示答案。

样例输入

 0
 4
 4 1 2 3 
 2
 1 1 
 1 2

样例输出

 2
 10
 6

数据范围

\(1 \le n \le 2 * 10^{5}, 0 \le q \le 2 * 10^{5}, 1 \le a_{i}, y \le 2 * 10^{5}, 1 \le x \le n\) 。

题解

Code

T3

题目描述

有一棵 \(n\) 个节点的树，一条树边可以记为 $(u_{i}, v_{i}, w_{i}),表示连接点 \(u_{i}\) 和点 \(v_{i}\) 权为 \(w_{i}\)。

对于边 \(i\) , \(a_{i,j}\) 的定义如下：令 \(c_{j,i}\) 为点 \(j\) 与其他 \(n - 1\) 个点之间的简单路径中经过边 \(i\) 的路径数，那么 \(a_{i,j} = c_{j,i} * w_{i}\) 。

一条边 \(i\) 在点 \(j\) 是优的，当且仅当不存在有另一条边 \(k\) 使得 \(a_{k,i} > a_{i,j}\)（可能有多条边在同一个点是优的）。

令 \(f(i)\) 表示边 \(i\) 在多少个点上是优的，现在要求 \(f(i)\) 。

输入格式

第一行，一个正整数 \(n\) 。

接下来 \(n - 1\) 行，每行三个正整数 \(u_{i}, v_{i}, w_{i}\) 表示一条边的信息。

输出格式

为减少输出量，共输出一行，一个整数，表示所有 \(f(i)\) 的异或和。

样例输入

 5
 1 2 3
 2 3 1
 3 4 1
 3 5 1

样例输出

 2

数据范围

\(n \le 10^{7}, w_{i} \le 10^{10}\)

题解

Code

T4

题目描述

GreenDuck 买到了最新的扫地机器人——RobotDuck。为了更高效地清扫房间，GreenDuck 决定分析一下房间的布局和 RobotDuck 的清扫机制。

GreenDuck 的房间可以看成是
行 列的网格，每个格子中要么是空的，要么放了一件家具。同时他惊奇地发现，每个家具都很薄(可以看成是一条线段)，两个端点分别占据了一个格子的西北角和东南角！

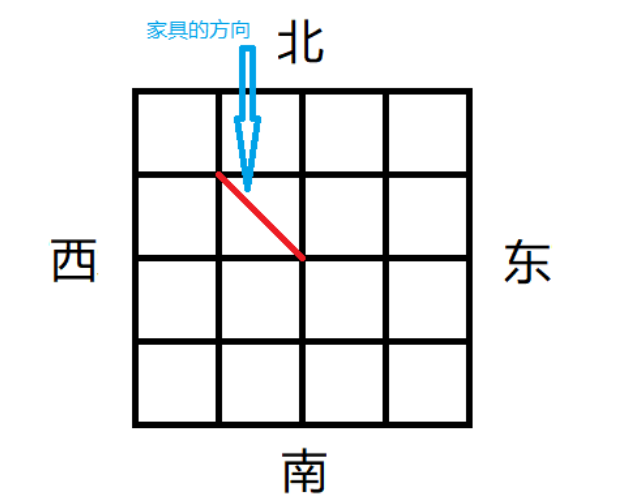
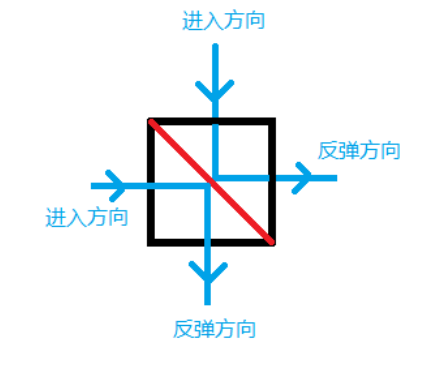
RobotDuck 在清扫时会采取这样一种机制：刚开始，可以给它设定一个方向(向南或向东)，接着它将一直沿着直线行进。如果碰到一个家具，那么会反弹。具体方式如下图所示。

GreenDuck 一开始得知，在自己的房间里有 \(k\) 件家具，第 \(i\) 件家具在第 \(x_{i}\)行，\(y_{i}\) 列。接下来，他会进行 \(Q\)次测试。

第一种测试，是在一个没有家具的格子上放上一件家具(方向保持一致)。这种测试后，他不会拿走任何家具。

第二种测试，是将 RobotDuck 贴着墙壁然后释放。具体来说，如果 RobotDuck 放在北面(对应了图中矩形的上边界)，那么它会从第一行某个格子的上边界的中心出发，面向南面行进。如果 RobotDuck 放在西面(对应了图中矩形的左边界)，那么它会从第一列某个格子的左边界的中心出发，面向东面行进。在行进过程中，它遵守清扫的机制。

GreenDuck 想知道，在每次第二种测试时，RobotDuck 在反弹恰好 \(q\) 次后会在哪个格子里。请你告诉他。

输入格式

第一行四个数字，\(type, n, m, k\), 分别表示数据类型(你可能不需要)，行数，列数，一开始有的家具件数。

接下来 \(k\)行，每行两个整数\(x_{i}, y_{i}\)，分别表示这件家具的行数和列数。

接下来一行一个整数 \(Q\) ，表示测试的次数。

接下来 \(Q\) 行，首先输入一个数字 \(w\)。

若 \(w\) 为 \(1\) ，则会有两个数字 \(x,y\)，分别表示新添的家具的行数和；列数。

若 \(w\) 为 \(2\)，则会有三个数字 \(x, y\)。若 \(x = 0\)，表示RobotDuck 从第一行第 \(y\)列格子的上边界的中心面向南行进。否则 \(y = 0\)，表示 RobotDuck 从第一列第 \(x\) 行格子的左边界的中心面向东行进。 \(q\) 表示反弹的次数。

输出格式

对于每个 \(w = 2\) 的操作，输出一行两个数字 \(x\) 和 \(y\)分别表示所在格子的行数和列数。

特别地，若 RobotDuck 在第 \(q\) 次反弹之前就碰到了墙壁，若墙壁是第 \(n\) 行格子的下边界，输出" \(n + 1\)列数"，否则输出"行数 $ m + 1$ "。

样例输入

 0 4 4 1
 2 2
 5
 2 2 0 3
 1 3 2
 2 2 0 2
 2 2 0 3
 2 2 0 4

样例输出

 5 2
 3 2
 3 5
 3 5

样例解释

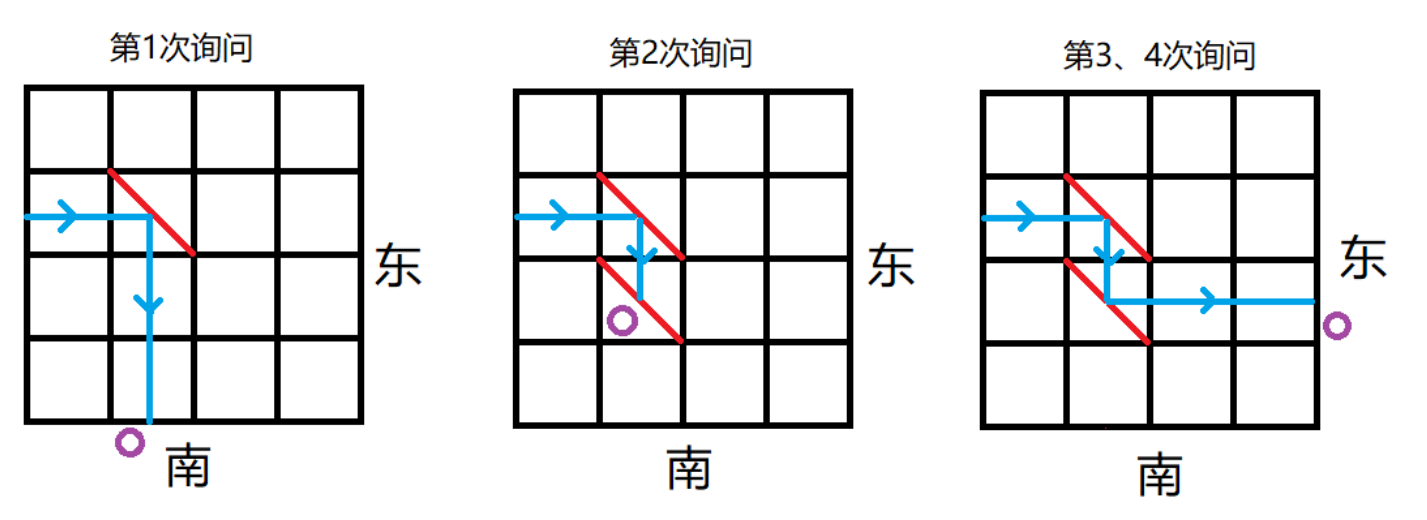
数据范围

对于所有数据，家具的坐标不会重复，每次第二种操作要么 \(x=0\) 要么 \(y=0\)。 \(1 \le q \le 200000\)。

题解

对于每一个格子来说建立两个点，分为上半部分和下半部分。然后分别对外连边。于是每一次查询就是相当于查询弹了 \(q\) 次后所到达的地方。
在这里的路径要记录弹了的次数。方便之后的查询。
关于加家具的操作可以考虑上面所说的上下两部分， 然后交换连一下， 还是很好处理的。
本来一个点的 上半部分由别人上部分向右连的， 加了家具之后就是从别人的下部分向下连， 另外半边也是一样。
涉及到单点交换修改， 且每一条路径都是链的情况下我们可以考虑使用链表经行处理。
不过要么修改时间复杂度高达 $ O(n) $, 要么查询的时间复杂度高达 $ O(n) $
于是考虑分块， 再结合基本不等式可以得出最优的分块数在 \(300\) 左右。
然后注意点细节什么的就好了。

Code

Day 3

上午的题目还可以， T1 拓扑排序但是写挂了 T2 数据结构还是挂了 T3 网络流 但是好像还是寄了 T4看都没看

T1

题目描述

对于计数问题和期望问题，你们⼀定都不陌⽣。
给定⼀个 \(n\)个点 \(m\) 条边的有向⽆环图，第 \(i\) 条边有\(p_{i}\) 的概率存在，另外 \(1-p_{i}\) 的概率不存
在，求从 \(1\) ⾛到 \(n\) 的路径条数的期望。

输入格式

第⼀⾏两个正整数 \(n\) 和 \(m\)，表示点数和边数。
之后m⾏，每⾏三个数 \(u_{i},v_{i},p_{i}\)，表示每条边的起点，终点和出现的概率。

输出格式

⼀个⼩数，表示路径条数的期望，保留2位⼩数。

样例输入

 3 3
 1 2 0.5
 2 3 0.5
 1 3 0.5

样例输出

 0.75

数据范围

\(n,m<=10^{5}\)，对所有 \(1<=i<=m\) ，满⾜ \(0<pi<1\) ，\(p_{i}\)⾄多两位⼩数。
保证给定的有向图不存在环，保证答案不超过100（不需要考虑精度问题）

题解

拓扑排序， 直接搞就可以， 转移就是每个点的期望到达值再乘上边的存在值。
最后用加法原理合并。
记得一开始拓扑的时候要把所有入度为零的点加进去。
虽然除了1以外其他点的贡献为零， 但是他们可以帮助别的点减少入度。（我在考试时就在这里寄了。）

Code

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 +100;
double ans[N];
struct T{
	int v;
	double val;
}; 
vector <T> tu[N];
int ru[N];
int n, m;
int main(){
	scanf("%d%d", &n, &m);
	for(int i = 1; i <= m; i ++){
		int u, v;
		double val;
		cin >> u >> v >> val;
		tu[u].push_back({v, val});
		ru[v] ++;
	}
	queue <int> q;
	for(int i = 1; i <= n; i ++)
		if(!ru[i]) q.push(i);
	ans[1] = 1;
	while(!q.empty()){
		int u = q.front();
		q.pop();
		for(int i = 0; i < tu[u].size(); i ++){
			int v = tu[u][i].v;
			double val = tu[u][i].val;
			ans[v] += (ans[u] * val);
			ru[v] --;
			if(!ru[v])
				q.push(v);
		}
	}
	cout << fixed<< setprecision(2) << ans[n];
	return 0;
} 

T2

题目描述

给定⼀个 \(n\) 个点堆（不⼀定是⼆叉堆）的结构，每个点的值构成 \(1 \sim n\) 的排列，即每个点的
值都是 \(1 \sim n\) 之间的整数，且任意不同的两点的值不同。根据堆的定义，每个点的值⼤于它的
所有⼦节点。
现在已知其中 \(k\) 个点的值，你需要回答是否存在这样的堆，即是否可能填上剩下 \(n-k\) 个点
的值，使得每个点的值是 \(1 \sim n\)的排列，并且满⾜每个点的值⼤于⼦节点。
你需要分别判定 \(T\) 棵堆。

输入格式

第⼀⾏⼀个正整数 \(T\) 。接下来有 \(T\) 组数据。
每组数据第⼀⾏两个正整数 \(n\)
第⼆⾏ \(n\) 个整数，表示这个堆上每个节点的⽗亲 \(f\)，如果 \(f_{i}=0\) 表示根是 \(i\)
第三⾏ \(n\) 个整数，表示每个节点的值 \(v_{i}\)，如果 \(v_{i}=0\) 表示该节点的值未知

输出格式

\(T\) ⾏，第 \(i\) ⾏表示第 \(i\) 组数据是否存在这样的堆，如果存在，输出 \(1\) ，如果不存在，输出0。

数据范围

\(T<=100,n<=10^4\)

样例输入

 2
 5
 0 1 2 3 4
 5 4 3 1 2
 13
 0 1 1 1 2 2 2 3 3 4 4 8 8
 13 7 9 0 0 0 0 3 0 0 0 0 0

样例输出

 0
 1

题解

Code

T3

题意描述

⼤学⾥总共有 \(c\) ⻔课，\(t\) 个时间段。每⻔课会在很多时间段开课，且不同时间段开的同⼀
⻔课可能容纳的⼈数不同，具体地，第 \(j\) 个时间段的第 \(i\) ⻔课的⼈数上限是 \(a[i,j]\)，如果\(a[i,j]=0\) 则表示该时间段不开放该课程。教室可以容纳的的⼈数最⼤值是 \(N\) ，保证所有的 $ a[i,j]<=N$ 。
每个学⽣每⻔课可以选择在任何⼀个时间段上，但不能在同⼀个时间段上超过⼀⻔课。求⼤
学⾥学⽣⼈数的上限，使得存在⼀种选课的⽅式，每位学⽣的每⻔课都能选上。

输入格式

第⼀⾏三个正整数 \(N\)，\(c\) 和 \(t\)，分别表示教室⼤⼩，课程数量和时间段数量。
之后 \(c\) ⾏，每⾏ \(t\) 个⾮负整数，第 \(i\) ⾏第 \(j\)个整数 \(a[i,j]\) 表示第 \(i\) ⻔课在第 \(j\) 个时间段的⼈数上限。

输出格式

⼀个⾮负整数，表示⼤学⾥学⽣⼈数的上限。

数据范围

$ N,c,t<=50 $

样例输入

 3 2 3
 3 1 0
 3 1 0

样例输出

 2

题解

Code

T4

题意描述

给定⼀张 \(n\) 个点 \(m\) 条边的⽆向图，求出所有⽣成树中，以 \(1\) 为根的情况下所有节点的深
度之和的最⼤值，其中树上节点的深度表示该节点到根的路径上的节点个数，包括该节点本身和根节点。

输入格式

第⼀⾏两个正整数 \(n\) 和 \(m\) ，表示点数和边数。
之后 \(m\) ⾏，每⾏两个整数 \(u\) 和 \(v\) ，表示每条边的端点。

输出格式

⼀个整数，表示所有节点深度之和的最⼤值。

数据范围

$ n \le 20, m \le n * (n - 1) / 2$

样例输入

 3 3
 1 2
 1 3
 2 3

样例输出f

 6

题解

Code

下午

下午讲图论

T1 ABC262E

T2 CSP-S2021交通规划

T3 Noi2022 挑战 NPCll （【模板】树同（[BJOI2015]
树的同构））

T4 CCO2022 P5 Phone Plans

T5 ABC261Ex

T6 AGC056C

T7 CF1519F

T8 CF1525F

T9 CF1508C

T10 CF1712F

Day 4

上午
只会T1, 其他的全不会

T1 Doctor

题目描述

给定一棵 \(n\) 个点的树和参数 \(k\)，你需要找到一条起点为 \(1\) 的路径，满足路径上恰好有 \(k\) 个不同的顶点，且路径的长度最短。一条路径的长度定义为路径经过的点数。

注意，你不需要保证路径是一条简单路径，即路径可以经过重复点和重复边。

输入格式

本题有多组数据。
输入的第一行包含一个正整数 \(T\)，分别表示测试数据组数。

对于每一组测试数据：
输入的第一行包含两个正整数 \(n , k\)，分别表示树的顶点数和要求经过的不同的顶点数。

接下来 \(n - 1\) 行，每行两个整数 \(u, v\)，表示树上存在一条连接顶点 \(u\) 和顶点 \(v\) 的边。

输出格式

对于每一组测试数据：
第一行包含一个正整数 \(m\)，表示路径的长度。

第二行包含 \(m\) 个正整数，描述树上的一条路径，其中第 \(i\) 个正整数表示路径上第 \(i\) 个结点的编号。

数据范围

$ 1 \le n, m \le 10^{5} $

样例输入

 2
 6 4
 1 4
 2 5
 1 6
 1 3
 1 2
 6 4
 1 2
 5 6
 1 4
 2 5
 1 3

样例输出

 5
 1 4 1 2 5 
 4
 1 2 5 6 

题解

Code

T2 Patriot

题目描述

给定 \(m\) 个集合 $S_1 \sim S_m $，计数长度为 \(n\) 的整数序列 \(a\)的个数，使得对于任意 \(i\)，$ 0 \le a_i \le r $ 且由 \(a\) 导出的长度为 \(m\) 的序列 $ b_i = \bigoplus\limits_{j \in S_i}a_j$ 是一个不降序列（定义空集的 \(b_i\) 为 $ 0 $），即对于 $ 1 \le i < m，b_i \le b_{i + 1} $。其中 $ \oplus$ 表示异或运算。

由于答案可能很大，请输出答案 \(mod\) $998244353 $ 的值。

输入格式

第一行包含两个整数 \(n，m\)表示序列长度和集合的个数。
接下来 \(n\) 行，每行包含一个用二进制形式表示的正整数，其中第 \(i\) 行的正整数表示 \(r_i\) ，含义见题目描述。

接下来 \(m\) 行，每行包含长度为 \(n\) 的 01 串，第 \(i\) 行描述集合 \(S_i\) ，其中第 \(i\) 个序列的第 \(j\) 个字符为 \(1\) 表示 $ j \in S_i$，为 \(0\) 表示 \(j \not\in S_i\)。

输出格式

一行一个整数，表示答案 \(mod\) \(998244353\) 的值。

数据范围

$ 1 \le n, m \le 7, 1 \le r_i \le 2^{500} - 1$

样例输入

 3 4
 110
 101
 100
 111
 101
 011
 010

样例输入

 10

题解

Code

T3 Talulah

题目描述

给定一个长度为 \(n\) 的排列 \(p\) ，定义集合 \(S_i = \{ x | x \ge i \enspace \max\limits_{i \le k < x} p_k < p_x \}\) 。你需要回答一共 \(q\) 组询问，对于第 \(i\) 组询问，给定区间 $ [l_i, r_i] $，你需要求出 $ \sum\limits_{l \le x, y \le r} |S_x \cup S_y|$的值。

输入格式

第一行包含三个正整数 \(n, 1, type\) ，表示排列的长度，询问次数以及 \(p\) 是否随机生成（ \(type = 1\)表示 \(p\) 随机生成）。

第二行包含 \(n\) 个正整数，描述排列 \(p\) ，其中第 \(i\) 个正整数表示 \(p_i\) 的值。

接下来 \(q\) 行，每行包含两个正整数 \(l_i，r_i\) 描述一组询问。

输出格式

共 \(q\) 行，其中第 \(i\) 行包含一个正整数，表示第 \(i\) 组询问的答案。

数据范围

$ 1 \le n, q \le 2,5 * 10^{5} $

样例输入

 5 5 0
 3 1 4 5 2
 1 2
 3 5
 2 5
 1 3
 1 5

样例输出

 14
 18
 41
 28
 72

题解

Code

T4 Rosmontis

题目描述

求有序正整数序列对 \((A,B)\) 的数量，满足 \(A_i，B_i \in [1,k]\) ,$ |A| = |B| = n $且存在方案使得从 \(A\) 中删去至多两个元素， \(B\) 中删去至多两个元素后，满足 \(A=B\)。

由于答案可能很大，请输出答案 \(mod \enspace 10^{9} + 9\)的值。

输入格式

第一行包含两个正整数 \(n, k\)，分别表示序列的长度和序列的值域。

输出格式

一行一个整数，表示答案模 $ 10^9 + 9$ 的值。

数据范围

$ 1 \le n, k \le 10^9 $

样例输入1

 3 3

样例输出1

 687

样例输入2

 4 7

样例输出2

 2165779

题解

Code

Day 5

T1 equal

上午一道题目都不会， 题目又没有好好讲的， 感觉最近有点寄。

题目描述

有一个长度为 \(n\) 的序列，你要切三刀，把这个序列分成连续的 \(4\) 段，每段的权值
为这段所有数之和, 你要让这四个权值的极差最小。

输入格式

第一行一个整数 \(n\) 。
第二行 \(n\) 个整数，第 \(i\) 个数为 \(a_i\)。

输出格式

一个整数表示最小的四段的极差。

数据范围

$ 4 \le n \le 200000, \enspace 1 \le a_i \le 10^9 $

样例输入

 5
 3 2 4 1 2

样例输出

 2

题解

其实本题很简单（但是在考试的时候没有想到）。
先枚举中间点， 然后把东西分成两部分， 然后再对两部分进行操作。
显然那两部分的极差最小时整体的极差最小, 可以用二分来做。
然后可以发现， 当中间点向左移动一格时， 左右两边的断电也至多会向右移动一格， 所以可以在线性时间内通过此题。

Code

#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 100;
int n;
long long a[N]; 
long long asum[N];
long long get(int l, int r){
	long long ll = l, rr = r;
	while ( ll < rr){
		int mid = (ll + rr) >> 1;
		if(asum[mid] - asum[l - 1] < asum[r] - asum[mid])
			ll = mid + 1;
		else 
			rr = mid;
	}
	return ll;
}

long long check(int l, int mid, int r){
	long long len[5];
	len[1] = asum[l], len[2] = asum[mid] - asum[l], len[3]= asum[r] - asum[mid], len[4]= asum[n] - asum[r];
	sort(len + 1,len + 1 + 4);
	return len[4] - len[1];
}
int main(){
	cin >> n;
	asum[0] = 0;
	for(int i = 1; i <= n; i ++)
		cin >> a[i], asum[i] = asum[i - 1] + a[i];
	int mid = 2;
	int l, r; // 规定第一段的值为 asum[l] 第二段为 asum[mid] - asum[l] 第三段为 asum[r] - asum[mid]  第四段为 asum[n] - asum[r] 
	long long ans = 0x3f3f3f3f3f3f3f3f; 
	for(mid = 2; mid <= n - 1; mid ++){
		int ll= get(1, mid), rr = get(mid + 1, n);
		for(int i = -1; i <= 1; i ++)
			for(int j = -1; j <= 1; j ++){
				int cl = ll + i, cr = rr + j;
				ans = min(check(cl, mid, cr), ans); 
			} 
	}
	cout << ans;
	return 0;
} 

T2 dance

题目描述

有一个长度为 \(n\) 的序列，对于序列中的每一个数你都需要求出，所有包含这个数
且长度在 \(l\) 到 \(r\) 范围内的连续子序列中，最大的连续子序列的权值和。

输入格式

第一行三个整数 \(n\), \(l\), \(r\)。
第二行 \(n\) 个整数，第 \(i\) 个数为 \(a_i\)。

输出格式

一行 \(n\) 个整数，第 \(n\) 个整数表示 \(f_i\)。

数据范围

$ 1 \le l \le r \le n \le 10^5, \enspace 0 \le |a_i| \le 10^5$

样例输入

 5 1 3
 -1 -6 7 7 -4

样例输出

 0 8 14 14 10

题解

Code

T3 practice

题目描述

你有一个数 \(a\)，你想要把它变成 \(b\) ，每次你可以选择一个 \([1, k]\) 范围内的整数 \(x\)，假
设当前的数为 \(p\)，你可以把 \(p\) 变成 \(p - (p \enspace mod \enspace x)\)，特别的，当你选择 \(x = 1\) 时，\(p\) 会变成 \(p - 1\) ，问你至少使用多少次操作才能把 \(a\) 变成 \(b\)。

输入格式

一行一个整数 \(T\)，表示有 \(T\) 组数据。
接下来 \(T\) 行每行 \(3\) 个数 \(a\), \(b\), \(k\)。

输出格式

输出 \(T\) 行每行一个整数表示答案。

数据范围

\(1 ≤ T ≤ 10，\enspace b ≤ a ≤ 10^{18}，\enspace 1 ≤ k ≤ 15\)。

样例输入

 3
 10 1 4
 6 3 10
 1000000000000000000 1 3

样例输出

 6
 2
 666666666666666667

题解

Code

T4 subsets

题目描述

给定一个由整数组成的集合，问有多少个非空子集，子集中的数能划分成和相等的
两份。集合中的数是可以重复的。

输入格式

一行一个整数 \(n\)，集合的大小。
接下来 \(n\) 行，第 \(i + 1\) 行的数 \(a_i\) 表示集合里第 \(i\) 个数。

输出格式

行一个数，表示方案数。

数据范围

$ n \le 20, \enspace |a_i| \le 10^8 $

样例输入

 4
 1
 2
 3
 4

样例输出

 3

题解

考试的时候总觉得像背包， 因为看错题目了。
其实只要输出可行的子集， 而我看成了具体的方案数， 导致写了一个很烦的背包然后成功保灵。
其实就是简单的状压加折半搜索。
可以考虑我们要把一个子集分成两个集合 \(A\) 和 \(B\)， 然后记 \(A\) 中元素总和 减去 \(B\) 中元素总和为 \(s\)。
然后考虑一个元素 \(a_i\) , 以及当前状态 \(sta\) ,有三种情况：

1. 不选， 对 \(s\) 和 \(sta\) 都没有影响
2. 选， 放进 \(A\) , \(s + a_i , sta \enspace | \enspace (1 << (i - 1))\)
3. 选， 放进 \(B\) , \(s - a_i , sta \enspace | \enspace (1 << (i - 1))\)

然后就处理出了半部分所有差值为 \(s\) 的状态 然后Hash一下， 后面要用。
思考， 前半部分差值为 \(s\) 后半部分差值为 \(-s\) 的两种分法合并在一起是不是就可以了。
所以在后半段结束时调用出之前Hash进的相应状态， 再取或运算， 这就是合法的状态。
因为每种子集只算一次， 考虑把合法的状态存进一个 \(bool\) 数组。
最后的答案就是把 \(bool\) 数组里的 \(1\) 全部加起来。
记住， 不能有空集。

Code

#include <bits/stdc++.h>
using namespace std;
int n;
const int N = (1 << 20) + 114514;
map <int, int> id;
int cnt = 0;
vector <int> Hash[N];
#define ll long long
ll a[23];
bool an[N];
int mid;
void dfsl(int dep, int s, int state){
	if(dep == mid + 1){
		if(!id[s]) id[s] = ++ cnt;
		Hash[id[s]].push_back(state);
		return;		
	}
	dfsl(dep + 1, s, state); //不选
	dfsl(dep + 1, s + a[dep], state | (1 << (dep - 1)));
	dfsl(dep + 1, s - a[dep], state | (1 << (dep - 1)));
}
void dfsr(int dep, int s, int state){
	if(dep == n + 1){
		if(!id[s]) return ;
		int k = id[s];
		for(int i = 0; i < Hash[k].size(); i ++)
			an[state | Hash[k][i]] = 1;
		return;
	}
	dfsr(dep + 1, s, state); //不选
	dfsr(dep + 1, s + a[dep], state | (1 << (dep - 1)));
	dfsr(dep + 1, s - a[dep], state | (1 << (dep - 1)));
}
int ans = 0;
int main(){
	scanf("%d", &n);
	for(int i = 1; i <= n; i ++)
		scanf("%lld", &a[i]);
	mid = n / 2;
	dfsl (1, 0, 0); 
	dfsr (mid + 1, 0, 0);
	for(int i = 1; i <= (1 << n); i ++)
		ans += an[i];
	cout << ans;
	return 0;
}

Day 6

T1

题目描述

小Q和小王在博弈。
对于所有 $ 1 \le i \le n$，桌子上有 \(a_i\) 个数字 \(i\)。 小Q和小王轮流操作，小Q先手。每次操作可以选任意两个相等的数 \(x\)，从桌子上拿走这两个数，并再放入一个 $ x + 1 $。
无法操作的人就输了。如果两人都采取最优策略，问谁会赢。
一个测试点含有多组数据。

输入格式

第一行一个整数 \(T\)，表示测试组数。
接下来 \(T\) 组每组第一行一个整数 \(n\)，第二行 \(n\) 个整数表示 \(a_1, a_2 , ...a_n\)

输出格式

\(T\) 行，每行一个大写字母表示该组测试的答案。若小Q会赢输出 \(Q\) ，否则输出 \(W\) 。

数据范围

$ T \le 10, /ensapce n \le 10^5, \enspace 0 \le a_i \le 10^9$

输入样例

 2
 1
 2
 2
 2 1

输出样例

 Q
 W

题解

这道是个诈骗题， 看上去是博弈论其实不是。
可以发现，这个游戏跟决策没有关系， 因为只要拿两个就可以。只要考虑总的操作次数就可以。
每一次操作会对后面一堆有影响， 所以从前往后做。
再注意 \(n\) 后面的数可能对答案也有贡献， 加上去就可以。
每一次做要将数组清零。

Code

 #include <bits/stdc++.h>
using namespace std;
int T;
#define ll long long
const int N = 2e5 + 100000;
ll a[N];
void solve(){
	int n;
	memset(a, 0, sizeof(a));
	scanf("%d", &n);
	for(int i = 1; i <= n; i ++)
		scanf("%lld", &a[i]);
	ll res = 0;
	for(int i = 1; i <= n; i ++){
		res += a[i] / 2;
		a[i + 1] += a[i] / 2;
		res %= 2;
	}
	int k = n + 1;
	while(a[k]){
		res += a[k] / 2;
		a[k + 1] = a[k] / 2;
		k ++;
		res %= 2;
	}
	if(res) printf("Q\n");
	else printf("W\n");
}
int main(){
	freopen("a.in", "r", stdin);
	freopen("a.out", "w", stdout);
	scanf("%d", &T);
	while (T --)
		solve();
	return 0;
} 

T2

题目描述

你有一个长度为 \(n\) 的序列 \(a_1, a_2...a_n\) 。
你需要进行 \(m\) 次操作。

1. 给定 \(p\)，\(x\) 将 \(a_p\) 赋值为 \(x\)。
2. 给定 \(l, r, k\) 将所有 \(l \le i \le r\) 的 \(a_i\) 赋值为 \(a_i \enspace mod \enspace k\)。（ \(mod\) 为取模运算）
3. 给定 \(l，r\) 求所有 $l \le i \le r $ 的 \(a_i\) 的最大值。

输入格式

第一行两个整数 \(n, m\)。
第二行 \(n\) 个整数 \(a_1, a_2, ... , a_n\)。
接下来 \(m\) 行每行第一个整数表示操作类型，后面 \(2\) 或 \(3\) 个整数表示这次操作给定的参数。

输出格式

对于所有操作 \(3\)，输出一行一个整数表示这次操作的答案。

数据范围

\(n, m \le 10^5, 1 \le a_i, x, k \le 10^9, 1 \le l \le r \le n\)。

输入样例

 3 5
 2 3 3
 3 1 3
 2 2 3 2
 3 1 3
 1 2 5
 3 2 3

输出样例

 3
 2
 5

题解

线段树， 暴力操作。
若子树的最大值小于模数， 就不去修改。

Code

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 1e5 + 1000;
int n, m;
struct Tr{
	ll val;
}tr[N * 8];
ll a[N];
void push_up(int rt){
	tr[rt].val = max(tr[rt << 1].val, tr[rt << 1 | 1].val);
	return;
}
void build(int rt, int l , int r){
	if(l == r){
		tr[rt].val = a[l];
		return;
	}
	int m = (l + r) >> 1;
	build(rt << 1, l, m);
	build(rt << 1 | 1, m + 1, r);
	push_up(rt);
	return ; 
}

bool check(int rt, ll p){
	if(tr[rt].val < p) return false;
	return true;
}
void change(int rt, int l, int r, ll p, ll x){
	if(l == r){tr[rt].val = p; return;}
	int m = (l + r) >> 1;
	if(m >= x) change(rt << 1, l, m, p, x);
	else change(rt << 1 | 1, m + 1, r, p, x);
	push_up(rt);
}

void update(int rt, int l, int r, int L, int R, ll k){
	if(l == r){tr[rt].val %= k; return;}
	int m = (l + r) >> 1;
	if(L <= m && check(rt << 1, k)) update(rt << 1, l, m, L, R, k);
	if(m < R && check(rt << 1 | 1, k)) update(rt << 1 | 1, m + 1, r, L, R, k);
	push_up(rt);
}

ll query(int rt, int l, int r, int L, int R){
	if(L <= l && r <= R) return tr[rt].val;
	int m = (l + r) >> 1;
	ll ans = -19090;
	if(L <= m){
		if(tr[rt << 1].val == 0) ans = max(ans, (ll)0);
		else ans = max(ans, query(rt << 1, l, m, L, R));
	}
	if(m < R){
		if(tr[rt << 1 | 1].val == 0) ans = max(ans, (ll)0);
		else ans = max(ans, query(rt << 1 | 1, m + 1, r, L, R));
	}
	return ans;
}
int main(){
	freopen("b.in", "r", stdin);
	freopen("b.out", "w", stdout);
	scanf("%d%d", &n, &m);
	for(int i = 1;i <= n; i ++)
		scanf("%lld", &a[i]);
	build(1, 1, n);
	for(int i = 1; i <= m; i ++){
		int pos;
		scanf("%d", &pos);
		if(pos == 1){
			ll p, x;
			scanf("%lld%lld", &p, &x);
			change(1, 1, n, x, p);
		}
		if(pos == 2){
			int l, r;
			ll k;
			scanf("%d%d%lld", &l, &r, &k);
			update(1, 1, n, l, r, k);
		}
		if(pos == 3){
			int l, r;
			scanf("%d%d", &l, &r); 
			printf("%lld\n", query(1, 1, n, l, r));
		}
	}
	return 0;
}

T3

题目描述

给定 \(n\)，求所有长度为 \(n\) 的错排的逆序对数之和。
一个测试点含有多组数据。
答案对 $998244353 $取模。

输入格式

第一行一个整数 \(T\)，表示测试组数。
接下来 \(T\) 行每行一个整数 \(n\)。

输出格式

\(T\)行， 每行一个整数表示这组数据的答案。

数据范围

$ T \le 2 * 10^5 \enspace n \le 10^7 $

输入样例

 3
 2
 3
 114514

输出样例

 1
 4
 556483447

题解

Code

T4（TL = 3s）

题目描述

现在是晚上九点，小王准备为大家献歌一首。
小王要唱的歌的歌词可以抽象成一个长度为 \(n\) 的字符串 \(s\)，其中每个字符可能是大小写字母，数字，下划线。
(注：大小写相同字母视为不同的字符)
现在，小Q会进行以下 \(m\) 次操作，每次操作给定 \(l, r, t\):

1. 小Q为了让小王唱的更魔怔，把歌词的第 \(l\) 个字符到第 \(r\)个字符替换为长度为 \(r - l + 1\) 的字符串。
2. 小Q想检验小王唱的怎么样，让小王从第 \(l\) 个字符唱到第 \(r\) 个字符。他想知道在这个过程他总共会听到多少次 \(t\) 。即 \(t\) 在 \(s[l,r]\) 中共可重叠出现了多少次。
   由于训练小王唱歌不是一件轻松的事，所以小Q请你写一个程序来帮他训练小王并回答每次询问。

输入格式

第一行两个整数 \(n, m\)。
接着一行长度为 \(n\) 的字符串 \(s\)。
下面 \(m\) 行每行开头一个 \(1\) 或 \(2\)表示操作类型，然后是两个正整数 \(l,r\) 和一个字符串 \(t\)。

输出格式

对于每次 \(2\) 操作，输出一行表示答案。

数据范围

\(1 \le n, m \le 10^5, \enspace 1 \le k_1 \le 2 * 10^6, \enspace 1 \le k_2 \le 10^5\)
其中，\(k_1\) 为所有 1 操作中的 \(t\) 长度之和， \(k_2\) 为所有 \(2\) 操作中的 \(t\) 长度之和。

输入样例

 34 10
 JinWan9Dian_WHQChangGe_BuJianBuSan 
 2 1 34 an 
 2 6 33 an 
 1 1 10 aaaaaaaaaa 
 2 2 9 aaa 
 2 1 34 _ 
 1 11 20 abaabaabab 
 2 1 20 ab 
 2 1 20 aab 
 1 1 34 JinWan9Dian_WHQChangGe_BuJianBuSan 
 2 1 34 JinWan9Dian_WHQChangGe_BuJianBuSan

输出样例

5
3
6
2
4
3
1

题解

Code

Day 7

T1 permutation

题目描述

给两个大小为 \(n\) 的排列 \(p,q\)。
你需要给出另一个大小为 \(n\) 的排列 \(h * p * h^{-1} = q\) 满足 ，或判断不存在这样的排列 \(h\) 。
一些定义：

• \(p\) 是一个大小为 \(n\) 的排列当且仅当 \(p_i \in \{ 1, 2, ..., n \}\)，且 \(p_i\) 两两不同。
• 对于两个大小为 \(n\) 排列的 \(p，q\) 定义 \(h = p * q\)，其中 \(\forall i, h_i = q_{p_i}\) 。（注意，这里的定义可能与你所了解的定义不同）
• 对于一个大小为 \(n\) 的排列 \(p\)，定义 \(p^{-1}\)为 \(p\) 的逆元，其中 p^{-1}$ 满足 \(\forall i, (p^{-1})_{p_i} = i\)

输入格式

第一行一个正整数 \(n\)。
第二行 \(n\) 个正整数，\(p_i\) 表示 。
第三行 \(n\) 个正整数，\(q_i\) 表示 。

输出格式

第一行输出一个字符串“YES”或"NO"，表示是否有解。
如果存在解，第二行 \(n\) 个正整数，表示 \(q_i\)。

数据范围

$ 1 \le n \le 10^5$

样例输入1

 5
 2 1 5 3 4
 4 3 2 5 1

样例输出1

 YES
 3 1 2 5 4

样例输入2

 2
 1 2
 2 1

样例输出2

 NO

题解

其实很简单。
根据题目意思将上述等式展开， 可以得到 \(q_i = h^{-1}_{p_{h_i}}\)
由逆元定义得到 \(h_{q_i} = p_{h_i}\)。
写成 \(h[q[i]] = p[h[i]]\)。
换元 令 \(i = q[i]\), 得到 \(h[q[q[i]]] = p[h[q[i]]]\)
再通过等式进行替换得到
\(h[q[q[i]]] = p[p[h[i]]]\)
可以不断迭代下去。
可以考虑其实际含义， 会发现\(h\)的下标会形成一个环， \(h\) 的值也会形成一个环， 两个环的大小是相等的！ 然后对\(p,q\)分别搞一下， 注意合并的时候要对应起来。
不存在的话， 就是存在一个环找不到与他相等的环。

Code

#include <bits/stdc++.h>
using namespace std;
int n;
const int N = 1e5 + 1000;
int p[N];
int q[N];
int h[N];

bool vis[N];
queue <int> start[N];
vector <int> cyc; 
int main(){
	freopen("permutation.in", "r", stdin);
	freopen("permutation.out", "w", stdout);
	scanf("%d", &n);
	for(int i = 1; i <= n; i ++)
		scanf("%d", &p[i]);
	for(int i = 1; i <= n; i ++)
		scanf("%d", &q[i]);
	for(int i = 1; i <= n; i ++){
		if(!vis[i]){
			int u = i;
			int size = 0;
			while(!vis[u]){
				vis[u] = 1;
				u = q[u];
				size ++;
			}
			//cout << size << endl;
			start[size].push(i);
		}
	}
	memset(vis, 0,sizeof(vis));
	for(int i = 1; i <= n; i ++){
		if(!vis[i]){
			cyc.clear();
			int u = i;
			int size = 0;
			while(!vis[u]){
				vis[u] = 1;
				u = p[u];
				size ++;
				cyc.push_back(u);
			}
			/*cout << size << endl;*/
			if(start[size].empty()){
				cout << "NO";
				return 0;
			} else{
				int u = start[size].front(); start[size].pop();
				for(int i = 0; i < size; i ++){
					h[u] = cyc[i];
					u = q[u];
				}
			}
		}
	}
	cout << "YES";
	printf("\n");
	for(int i = 1; i <= n; i ++)
		printf("%d ", h[i]);
	return 0;
	}
/*
5
2 1 5 3 4
4 3 2 5 1
2
2 1
1 2
 */

T2 graph

题目描述

图论中常常有一些问题不能在一般图中快速解决，但是能在具有特殊性质的图中得到高效的解法。
最近你知道了一类新的图：线图。线图是由一个原图 \(G \enspace = \enspace <V, E>\)生成的。
对于无向图 \(G \enspace = \enspace <V, E>\)，它的线图 \(L(G)\) 也是一个无向图：

• 它的点集大小为 \(|E|\) ，每个点唯一对应着原图的一条边。
• 两个点之间有边当且仅当这两个点对应的边在原图上有公共点（注意不会有重边和自环）。
  给一个 \(n\) 个点 \(m\) 条边的简单无向图 \(G\)。
  请求出这张图的线图 \(L(G)\) 中的最大匹配。

输入格式

第一行两个正整数 \(n, m\)。
接下来 \(m\) 行，每行两个正整数 \(x, y\)表示一条边。
保证没有重边和自环。

输出格式

第一行一个数表示答案。

数据范围

$ 2 \le n \le 10^5, \enspace m \le 2 * 10^5$

样例输入1

 6 3
 1 2
 3 4
 5 6

样例输出1

 0

样例输入2

 5 4
 1 2
 2 3
 3 4
 4 5

样例输出2

 2

样例输入3

 6 9 
 1 2
 1 5
 2 5
 4 6
 3 4
 3 5
 1 6
 1 3
 2 4

题解

诈骗题。
手玩一下可以发现， 线图不可能是一棵树。
于是先建图（线图）， 然后可能会存在多个连通分量， 每个分量的(点数/2)， 再加起来就是答案。
感性理解， 考试的时候猜到了， 就对了。

Code

#include <bits/stdc++.h>
using namespace std;
const int N = 5 * 1e5 + 114514;
int n, m;
int fa[N];
int size[N];
int find(int x){
	if(fa[x] == x) return x;
	return fa[x] = find(fa[x]);
}
int ans = 0;
void merge(int x, int y){
	int cy;
	x = find(x), y = find(y);
	cy = y;
	if(x == y) return;
	fa[y] = x; //把y与x相连, 后面只会用到 x了
	size[x] += size[cy]; 
	return ;
}

bool vis[N] = {0};
int main(){
//	freopen("graph4.in", "r", stdin);
//	freopen("graph.out", "w", stdout);
	scanf("%d%d", &n, &m);
	for(int i = 1; i <= n; i ++)
		fa[i] = i;
	for(int i = n + 1; i <= n + m; i ++)
		fa[i] = i, size[i] = 1;
	for(int i = 1; i <= m; i ++){
		int u, v;
		scanf("%d%d", &u, &v);
		merge(u, i + n);
		merge(v, i + n);
	}
	
	for(int i = 1; i <= n + m; i ++){
		int f = find(i);
		if(vis[f]) continue;
		vis[f] = 1;
		ans += (size[f] / 2);
	}
	printf("%d", ans);
	return 0;
} 

T3 gcd

题目描述

考虑一个随机过程现在有 \(x \enspace = \enspace 0\)。
随机从选取 \([1,n]\) 中选取一个整数，并将 \(x \enspace = \enspace gcd(x, y)\) ，\(x\)求 第一次变成 \(m\) 的约数的期望选取次数。
注意 \(gcd(x, 0) \enspace = \enspace x\)。
由于 \(m\) 很大，我们将读入 \(m\) 的标准分解式。
输出答案对 \(998244353\) 取模的结果。

输入格式

第一行一个正整数 \(n\)。
接下来读入 \(m\) 的标准分解式。
第二行一个数 \(w\)。
接下来 \(w\) 行每行两个数 \(p_i,a_i\)。
保证 \(p_i\)互不相同且是质数， \(1 \le a_i,m = \prod\limits_{i = 1}^w p_i^{a_i}\) 。

输出格式

一行一个整数，表示答案对 \(998244353\) 取模的结果。

数据范围

$ 1 \le n \le 10^10 , 1 \le w \le 40, 2 \le p_i \le min(n, 10^9), 1 \le a_i \le log_{p_i}n$

样例输入1

 5
 0

样例输出1

 166374061

样例输入2

 4
 1
 2 1

样例输出2

 665496237

样例输入3

 100 
 2
 2 1
 5 1

样例输出3

 375580394

题解

Code

T4 ramsey

题目描述

本题是提交答案题。
本题来自FJOI2077，你需要解决的NP问题是计算Ramsey Number的下界。
为了给出下界，你需要构造一个点数尽量多的无向完全图，并给其中的每一条边染色，颜色数不超过 \(k\) ，使得没有同色三元环。

输入格式

本题为提交答案题。所有输入数据ramsey1.in,...,ramsey6.in，见sample/ramsey目录。
一行一个整数，表示颜色数 \(k\)。

输出格式

对于每组数据，你需要输出你的构造方案，保存在ramsey1.out,...,ramsey6.out里。
第一行输出一个数 \(n\) ，表示你构造图的点数。
接下来 \(n - 1\) 行，第 \(i\) 行 \(n - 1\)个整数：第 \(j\) 个整数\(c_{i, i + j}\) 表示边 \((i, i + j)\) 的颜色。
你需要保证 \(0 \le c_{i, i +j} \le k - 1\)。

数据范围

对于第 \(i\) 个测试点 有\(k = i\)。

1. \(k = 1 ,\enspace score = 6\)
2. \(k = 2 ,\enspace score = 10\)
3. \(k = 3 ,\enspace score = 13\)
4. \(k = 4 ,\enspace score = 20\)
5. \(k = 5 ,\enspace score = 23\)
6. \(k = 6 ,\enspace score = 28\)

样例输入

 3

样例输出

 3
 0 1
 2

题解

Code

Day 8

T1 card

题目描述

在一场会议上，参会的 \(N\) 个人 (编号为 \(1 · · · N\)) 决定互相交换名片。初始时，每个人手里都有恰好 \(N\) 张自己的名片。他们决定将名片交换的过程分为若干轮，在每一轮中，每个人 \(u\) 可以选择另一个人 \(v\)(可以是自己)，然后将自己手中任意数量的名片交给 \(v\)。名片交换完成后，他们希望每人手里恰好有来自每个人的名片各一张 (包括来自自己的)。

请你求出，至少需要几轮名片交换才能满足目标，并给出任意一种可行的方案。

输入格式

输入一行一个整数 \(N\) 表示总人数。

输出格式

第一行输出一个整数 \(M\) ，表示名片交换所需要的轮数。
接下来 \(M\) 行，每行 \(N\) 个数，第 \(i\) 行第 \(j\) 个数表示在第 \(i\) 轮中第 \(j\) 个人选择将部
分名片交给的人的编号。
接下来 \(N^2\) 行，每行一个长度为 \(M\) 的 01 串，其中第 \((i - 1) × N + j\) 行第 \(k\) 位表示原本属于 \(i\) 号，最终送到 \(j\) 号手里的名片在第 \(k\) 轮交换中有没有被它当前的持有者交给另一个人，有则为 1，没有为0。

数据范围

$ 1 \le N \le 1000$

样例

样例是错的然后我就5pts

题解

Code

T2 clique

题目描述

给定一张 \(N\) 个节点的图，其中第 \(i\) 个点的坐标为 \(x_i\)，权值为 \(w_i\)。两个点 \(i, j\) 之间
存在一条边当且仅当 \(abs(x_i - x_j ) \ge w_i + w_j\)。
请你求出这张图的最大团的点数。（团是任意两点间都存在边的顶点集合）

输入格式

第一行一个整数 \(N\)，表示图中点数。
接下来 \(N\) 行, 每行两个整数 \(x_i\), \(w_i\)，意义如上所述。

输出格式

输出一行一个整数，表示答案。

数据范围

\(1 \le N \le 2 * 10^5, 0 \le |x_i|, w_i \le 10^9\)

样例输入

 4
 2 3
 3 1
 6 1
 0 2

样例输出

 3

题解

考试的时候不知道为什么就爆零了。
赛后叫就过了，就先讲一讲我的做法。
首先看到式子， 不妨先令 \(x_i > x_j\),然后移项可得 ：
\(x_i - w_i \ge x_j + w_j\)
有什么用呢， 利用数学中的放缩有（\(w_i \ge 0\)）
\(x_i - w_i \ge x_j + w_j \ge x_j - w_j \ge x_k + w_k \ge ...\)
于是， 我们考虑将他们以 \(x_i + w_i\)从小到大排序。
如果 \(x_i - w_i \ge x_j + w_j\) 那么 \(i\) 就可以直接接在 \(j\) 后面使得答案增加。
这边可以直接考虑贪心， 因为越前面 \(x_i + w_i\) 越小， 越可能能收纳更多的东西。
然后用 \(tmp\) 记录当前的 $x_i + w_i $。

等等， 我们是不是忘了什么？ 没错这一切都是基于 \(x_i \ge x_j\)的！
考虑每一次接在后面的过程， 会有
\(x_i + w_i \ge x_i - w_i \ge x_j + w_j \ge x_j - w_j\)
然后前两项相加， 后两项相加,就得到了\(x_i \ge x_j\)！

Code

  #include <bits/stdc++.h>
using namespace std;
int n;
const int N = 2e5 + 10;
#define ll long long
struct T{
	ll x, y;
}a[N];
bool com(T a, T b){
	return a.y < b.y;
}
int main(){
	scanf("%d", &n);
	for(int i = 1; i <= n; i ++){
		int u, v;
		scanf("%d%d", &u, &v);
		a[i].x = u - v;
		a[i].y = u + v;
	}
	sort(a + 1, a + 1 + n, com);
	ll pre = a[1].y;
	int ans = 1;
	for(int i = 2; i <= n;i  ++){
		if(a[i].x >= pre){
			pre = a[i].y;
			ans ++;
		}
	}
	printf("%d", ans);
	return 0;
}

T3 division

题目描述

给定整数 \(N\)，请你在前 \(N\) 个正整数中选出尽可能多个，满足他们两两互不整除。在满足选出正整数数量尽可能多的前提下，请输出任意一个正整数总和尽可能小的方案。

输入格式

一行一个整数 \(N\)，表示输入。

输出格式

输出一行一个 01 串，第 \(i\) 位为 1 表示选择整数 \(i\)。

数据范围

\(1 \le n \le 2 * 10^7\)

样例输入1

 7

样例输出1

 0110101

样例输入2

 4

样例输出2

 0110

题解

Code

T4 mul

题目描述

无平方因子数指的是不能被任何一个质数的平方整除的数。给定 \(N, K\)，请你求出，
在 \(1 · · · N\) 中不重复地选出不超过 \(K\) 个整数相乘，使得乘积为无平方因子数，有多少种方案？答案对 \(10^9 + 7\) 取模。

输入格式

第一行一个整数 \(T\) 表示数据组数。
接下来 \(T\) 行，每行两个整数 \(N, K\)，意义如题面所述。

输出格式

对于每一组数据，输出一个整数表示答案对 \(10^9 + 7\) 取模后的值。

数据范围

\(1 \le T \le 10, 1 \le K \le N \le 500\)

样例输入

 3
 1 1
 6 4
 4 2

样例输出

 1 
 19
 6

题解

Code

Day 9

上午一道题都不会，纯坐牢。

T1 string

题目描述

给定两个 01 字符串（可重）集合 \(S\), \(T\)，求是否存在一个串\(H\)，满足：

1. 在\(S\)中存在至少两个不同的串\(s_i, s_j(i \ne j)\) 是 \(H\)的子串；
2. \(T\)中任意一个串 \(t_i\)都不是 \(H\)的子串。
   若存在这样的串，输出 Yes，否则输出 No 。
   本题多组数据。

输入格式

第一行一个正整数 \(K\)，表示数据组数。

对于每组数据，第一行两个正整数 \(n, m\)，分别表示 \(S\) 和 \(T\)中的字符串数目。

接下来 \(n\) 行，每行一个 01 串 ，表示集合 \(S\) 中的字符串。

接下来 \(m\) 行，每行一个 01 串 ，表示集合 \(T\) 中的字符串。

输出格式

\(K\) 行，每行一个字符串 Yes 或者 No，表示每组数据的答案。

数据范围

\(1 \le K \le 10^5, \sum n + \sum m \le 10^5, \sum |s_i| + \sum |t_i| \le 10^6\)

样例输入

 2
 3 2
 100
 001
 010
 1001
 000
 2 4
 100
 001
 010
 1001
 000
 11

样例输出

 Yes
 No

题解

Code

T2 sequence

题目描述

有一个长为 \(n\) 的序列，初始时候值均为 \(0\) ，小明昨天对这个序列进行了 \(m\) 次操作，每次操作的格式为：选取 \(a_i\) 个不同的位置，使得这些位置的值加上了 \(1\)。

然而一觉醒来，今天的小明已经不记得每次对哪些位置进行了操作，只记得每次的 \(a_i\)是多少。

他想要知道，对于给定的 \(n,m\)和每次操作的位置数目 \(a_i\)，在所有可能的最终序列中，值为 \(k\) 的位置最多有多少个？

对于 \(1 \le k \le m\) 都输出答案。

输入格式

第一行两个整数\(n,m(1 \le n, m \le 2*10^5)\) 分别表示序列长度和操作数目。
接下来一行 \(m\) 个数 \(a_1, a_2, ..., a_m\) 表示每次操作的位置数目。

输出格式

一行 \(m\) 个数 \(a_1, a_2, ..., a_m\)。

数据范围

\(1 \le n,m \le2 * 10^5, 1 \le a_i \le n\)。

样例输入1

 3 3
 1 2 3

样例输出2

 6 6
 2 2 3 3 4 4 

样例输出

 3 4 6 4 3 2

题解

Code

T3 digital

题目描述

众所周知，& | ！ (与或非） 是一套逻辑完备集，可以拼凑出各种你想要的真值表，从而实现各种 电路。但如果你手头没有非门元器件，& | 便不构成完备集，此时要拼出实现某些功能的电路便面临一些困难。

现在，给定 \(n\)个输入门，编号为 \(1 \sim n\)，每个输入门会输入 \(0\) 或者 \(1\)，然后将输入值放入输出端。你需要设计一个满足要求的电路，使得输出 \(n\) 个数的众数，即 \(0\) 和 \(1\) 中较多的那个，若数目一样，输出 \(1\)。

你手头有 \(5 * 10^4\) 个多输入与门，和 \(5*10^4\) 个多输入或门，他们的使用方法如下，设当前已经使用过的最大编号为 \(cnt\) ，初始时 \(cnt = n\)：

OR \(k \enspace a_1, a_2 ... a_k\):
将此元器件的输入端接入编号为 的元器件的输出端，此元器件输出端为这些值或起来的值，然后令 \(cnt + 1\)并作为这个元器件的编号。

AND \(k \enspace a_1, a_2 ... a_k\):
将此元器件的输入端接入编号为 的元器件的输出端，此元器件输出端为这些值与起来的值。然后令 \(cnt + 1\)并作为这个元器件的编号。

一个元器件的输出端可以被多个元器件调用。

另外，对于整个电路，我们还有以下限制：

1、\(\sum k \le 2*10^5\)；

2、整个电路的层数不能超过参数 \(d\)，所谓“层数”，定义为整个电路中最长的有向路径的长度(节点数目)，你可以通过样例理解这一点

当你拼接好了电路之后，输出一个 END，此时会取你电路中编号最大的元器件的输出端，作为你的答案，即你计算的 01 众数。

本题采用评测方式比较特殊，在你给出你构建的电路之后，\(Special Judge\) 会生成 \(1500\) 组不同的 01 输入分别进入 \(1 \sim n\) 的输入门，并检验你的电路输出是否正确，全部通过才会认为通过该测试点。保证随机种子是固定的，即所有选手在同一个测试点面临的数据都是相同的。

输入格式

一行两个参数 \(n，d\) 分别表示输入个数、深度限制。

输出格式

若干行，以字符串 END 结尾，其余每一行是以下两种格式之一，具体意义见题面：

1. OR \(k \enspace a_1, a_2 ... a_k\)
2. AND \(k \enspace a_1, a_2 ... a_k\)

数据范围

\(1 \le n \le 64, d \ge 14\)。

样例输入

 4 100

样例输出

 AND 2 1 2
 AND 2 1 3
 AND 2 1 4
 AND 2 2 3
 AND 2 2 4
 AND 2 3 4
 AND 3 5 5 6
 AND 1 7
 OR 6 5 6 7 8 9 10
 END

题解

Code

T4 coffee

题目描述

在接下来 \(n\) 天之中，每天咖啡店的价格是不同的，第 \(i\) 天咖啡的价格为 \(a_i\)。

你手上有 \(m\) 张优惠券，每张优惠券会在第 \(r_i\)天后过期（第 \(r_i\) 天时还可以使用），优惠券只能在购买咖啡的时候一并使用，从而使得那杯咖啡价格减少 \(w_i\) 元，一天最多使用一张优惠券。需要注意的是，由于老板并不聪明，咖啡的价格可以变成负数。

由于你最近出题很累，需要喝咖啡补充能量，但是过多的咖啡因不利于身体健康，所以你决定在这 \(n\) 天之中，选择恰好 \(k\) 天，购买咖啡。

请聪明的你合理的利用手上的优惠券，使得这 \(k\) 杯咖啡的价格加起来最小。

输入格式

第一行两个整数 $n,m，表示总天数与优惠券数量。

接下来一行 \(n\) 个整数，第 \(a_i\) 个整数 \(a_i\) 表示每天咖啡的价格。

接下来 \(m\) 行每行两个整数 \(r_i, w_i\) ，分别表示第 \(i\) 张优惠券的最晚使用时间与能减少的价格。

接下来一行一个整数 \(k\)，表示需要购买的咖啡杯数。

输出格式

一个整数 \(ans\) ，表示 \(k\) 杯咖啡的最小价格之和。

数据范围

$ 1 \le n \le 10^5, 1 \le m \le 2*10^5, 1 \le a_i, w_i \le 10^9, r_i \le n, k \le n$

样例输入1

 5 2
 1 2 3 4 5
 3 1
 4 2
 5

样例输出1

 12

样例出入2

 7 3
 4 3 1 10 3 8 6
 4 9
 3 8
 4 5
 5

样例输出2

 -5

题解

Code

Day 10

————今天ska_0x08身体不好， 由z代写

T1 naboo

题目描述

具体来说，加加宾会告诉你一个 \(1 \le v < n\)，你可以重新排列这些数，使得最终 \(a_1 + a_2 ... + a_v = a_{v+1} + ...+a_n\) 。
如果无法达成目标，你需要报告 \(-1\) ，否则，你需要求出最小的操作次数。一次操作是指交换任意的两棵树。
为了增加一些难度，加加宾会偷偷对 \(\{a_n\}\) 进行单点修改操作。在每次修改之后，你都需要对他当前给出的 \(v\) 进行回答。

输入格式

第一行，两个正整数 \(n,m\) 。
接下来一行， \(n\) 个正整数，依次表示 \(a_1 ... a_n\) 。
接下来 \(m\) 行，每行三个正整数 \(x,y,v\) ，表示将 \(a_x\) 修改为 \(y\) ，并作询问 \(v\) 。

输出格式

\(m\) 行，依次表示答案。

数据范围

对于所有数据， \(1 \le n , m \le 10^6 , 2 \le n\) ，保证 \(1 \le x \le n , 1 \le a_i , y \le 3\) 。

样例输入1

2 2
1 2
2 1 1
2 3 1

样例输出1

0
-1

样例出入2

6 4
1 2 3 3 3 3
6 2 3
4 1 2
3 1 2
1 3 5

样例输出2

1
2
1
-1

样例出入3

10 3
2 1 1 3 1 2 2 2 3 2

样例输出3

-1
5
1

T2 塔图因（tatooine）

题目描述

塔图因星球上有\(n\)座小镇，由 \(n − 1\) 条双向道路连接，形成一个联通无向图。
第i条道路连接小镇 \(A_i\) 和 \(B_i\) ，并且有一个容量 \(C_i\) ，表示运送货物的重量上限是 \(C_i\)千克。对于每两座小镇 \(x , y\) ，定义 \(F ( x , y )\) 表示从 \(x\) 向 \(y\) 能够一次性运送的货物重量上限值。
请你对于每条道路求出，在只断掉它而保留其他所有道路的情况下，所有\(F ( x , y )\)的总和。注意 \(( x , y )\) 是无序对，且 \(x \not = y\) 。如果连一千克货物都运送不了，那么 \(F ( x , y ) = 0\) 。

输入格式

第一行，一个正整数 \(n\) ，表示小镇个数。
接下来\(n − 1\)行，每行三个正整数，依次为\(A_i , B_i , C_i\)。

输出格式

共\(n − 1\)行，每行一个整数，表示断掉这条边之后的答案。
请按照边的输入顺序进行输出。

数据范围

对于所有数据，\(1 \le n \le 8×10^5,1 \le A_i \not = B_i \le n , 1 \le C_i \le 20\)。

样例见下发文件

T3 飞船竞赛（contest）

题目大意

竞赛一共进行 \(n−1\) 轮，每轮会从当前还在场上的选手中等概率随机选择两名，进行竞速比赛。水平更高者将以 \(p\) 的概率获胜， \(1−p\) 的概率失败，而败者会被直接淘汰。不存在平局等其他情况。
现在，安纳金想知道，对于每个选手来说，期望会度过多少轮？
注意：如果在某一轮中，该选手没有被选中，或者在这一轮被淘汰了，也会计入度过的轮数。可以结合样例进行理解。
与标准答案的绝对或相对误差在 \(10^{−6}\) 以下即视为正确。

输入格式

一行，两个数， \(n\) 和 \(p\) 。

输出格式

\(n\) 行，第 \(i\) 行表示编号为 \(i\) 的选手的答案。

数据范围

对于所有数据， \(1 \le n \le 8000,0.5 \le p \le 1.0\) ，保证输入的 \(p\) 小数点后最多 \(3\) 位。

样例输入1

2 1.0

样例输出1

1.0
1.0

样例出入2

3 1.0

样例输出2

1.33333333
1.66666667
2.00000000

样例出入3

4 1.0

样例输出3

1.666666667
1.944444444
2.388888889
3.000000000

样例出入4

3 0.5

样例输出4

1.666666667
1.666666667
1.666666667

样例出入5

10 0.618

样例输出5

4.87582118
4.97422389
5.07819620
5.18830806
5.30521511
5.42967545
5.56257027
5.70492931
6.02309818

T4 欧比旺（obiwan）

题目大意

欧比旺的工作是切割鲸鱼肉。他将高低不平的鱼肉抽象为一个\(n \times m\)的网格，位置 \((i,j)\) 处的高度用 \(H_{i,j}\) 表示。
为了使鱼肉变得更加湿润可口，欧比旺召唤来了乌云，干旱的沙漠上罕见地下起了雨。积水的高度将从 \(0\) 缓慢上升至 \(10^9\) 。
欧比旺认为，对于位置 \(( i , j )\) 处的鱼肉来说，只有当积水高度严格位于 \(S_{i,j}\) 和 \(S_{i,j+1}\) 之间的时候，它才可以被采集。当然，一个位置的鱼肉被采集过了就不能再被采集了。
不幸的是，鲸鱼实在是过于巨大了。欧比旺不得不召唤来一些机器人，帮助他采集鱼肉。
每个机器人都可以在网格上自由地走向四联通的位置，但是一旦所在位置的高度≤当前积水高度，机器人就会发生短路故障，停止工作。
你可以认为下雨的速度非常缓慢，缓慢到任意时刻都允许每个机器人行走任意多步。机器人都很小，所以一个位置上可以有多个机器人。
现在，欧比旺想知道，他最多可以采集到多少个位置的鱼肉？在达到这个最大值的情况之下，最少需要召唤多少个机器人？
此外，良心的出题人会对 \(S_{i,j}\) 进行 \(q\) 次单点修改，你需要在所有修改之前以及每次修改之后，都输出上面两问的答案。

输入格式

第一行，两个正整数 \(n,m\) 。
接下来 \(n\) 行，每行 \(m\) 个整数，表示 \(H_{i,j}\) 。
接下来 \(n\) 行，每行 \(m\) 个整数，表示 \(S_{i,j}\) 。
接下来一行，两个整数\(q\)和\(op\)。\(op=0\)表示不强制在线， \(op=1\) 表示强制在线。
接下来 \(q\) 行，每行三个整数 \(x,y,z\) ，表示将\(S_{x,y}\)设置为\(z\) 。
如果 \(op = 1\) ，那么 \(x,y,z\) 均需要异或上一次的第二问答案。
注意：对于第一次修改来说，上一次的第二问答案为 \(0\) ，即 \(q\) 行中的第一行 \(x,y,z\) 永远是真实值。

输出格式

\(q+1\) 行，每行两个整数，表示两问的答案。

数据范围

对于所有数据，\(1 \le n,m,n \times m \le 10^6, 1≤H_{i,j} \le 10^9,0 \le S_i,j \lt 10^9,0 \le q \le 10^6,1 \le x \le n,1 \le y \le m,0 \le z \lt 10^9\) 。

输入样例 1

1 3
98 99 100
97 98 99
1 0
1 1 98

输出样例 1

3 1
2 1

输入样例 2

2 3
5 2 4
3 2 1
3 3 3
3 3 3
5 1
1 2 2
3 3 3
3 3 0
0 2 3
3 0 3

输出样例 2

2 2
2 2
2 1
3 1
3 1
4 2

Day 11

T1 (TL = 2s)

题目描述

有 \(n\) 个数 \(a_1, a_2, ..., a_n\) 。保证 $ 1 \le a_i \le m $。
初始时有一个变量 $ X = 0$ 。你要进行 \(k\) 轮操作，每次操作可以任意选择一个 \(1 \le p \le n\)的 \(p\)，并将\(X\)
赋值为 \(gcd(X, a_p)\)。
（tips: \(gcd(0,x) = x\)）
问对于所有 \(1 \le i \le m\)，最终 $X = i $的方案数是多少。
两种方案不同，当且仅当存在一个 \(i\) ，满足两种方案第 \(i\) 轮选的 \(p\) 不同。
答案对 \(998244353\) 取模。

输入格式

第一行三个整数 \(n, m, k\)。
第二行 \(n\) 个整数 \(a_1, a_2, ... , a_n\)。

输出格式

一行 \(m\) 个整数，第 \(i\) 个表示最终 \(X = i\)的方案数。

数据范围

\(1 \le n, m \le 10^6, 1 \le k \le 10^9\)

样例输入

 6 6 2
 1 1 4 5 1 4

样例输出

 31 0 0 4 1 0

题解

Code

T2 (TL = 2s)

题目描述

初始时有一个 \(n\) 个点， \(0\) 条边的图。
你要进行 \(m\) 次操作：

1. 给定两个点编号 \(u, v\)和整数 \(w\)，在 \(u, v\)两个点之间加一条权值为 \(w\) 的边。
2. 给定一个点编号 \(u\)，求选取一条在 \(u\) 连通块内的路径，使得这条路径上所有边权的异或值最大。
   输出这个最大值。

保证任意时刻，图中都不会出现环。

输入格式

第一行两个整数 \(n, m\)。
接下来 \(m\) 行每行 \(1 u v w\) 或 \(2 u\) ，表示一次操作。

输出格式

对于所有 2 操作，输出一行一个整数表示答案。

数据范围

\(1 \le n \le 10^5, 1 \le m \le 2 * 10^5, 0 \le w \le 10^9\)

样例输入

 5 8
 2 2
 1 1 2 5
 2 1
 1 2 3 3
 2 1
 1 2 4 16
 2 4
 2 5

样例输出

 0
 5
 6
 21
 0

题解

Code

T3 (TL= 2s)

题目描述

有两组人在抢一块金条。两个组编号为 \(1\) 和 \(2\)， \(1\) 组的人从 \(1\) 到 \(n\) 编号，\(2\) 组的人从 \(1\) 到 \(m\) 编号。
初始时， \(P\) 组的 \(X\) 号人拿着金条，然后争夺之战一触即发。
在一轮中：

没拿金条的那组的所有还在场的人按照编号顺序由小到大进行决策：

1. 不去抢。此时什么事也不会发生，决策权给到下一个人。
2. 去抢。那么金条到他手里，原本持有金条的人遗憾离场，游戏立即进入下一轮。

如果编号最大的人都决策完了后金条还没被抢到，那么金条就归拿着的人所有了。

两组之间有 对人有私交，他们不会在任何情况下直接去抢对方手里的金条。

但一个人对于和他没有私交的人就可以任意决策。

每个人都第一希望拿到金条，在拿不到金条的情况下，他们第二希望不遗憾离场。

如果所有人都绝顶聪明，问最后每个人的情况是什么？
（情况分为三种：遗憾离场，在场但无金条，得到金条）

输入格式

第一行五个整数 \(n, m, P,X,k\) 。

接下来 \(k\) 行每行两个整数 \(a_i，b_i\) 表示 \(1\) 组的 \(a_i\) 号人和 \(2\) 组的 \(b_i\)号人有私交。

保证不存在两行描述一组相同的关系（即 \(a_i = a_j, b_i = b_j\)）。

输出格式

第一行 \(n\) 个用空格分隔的数字，表示 \(1\) 组每个人的最终情况。

第二行 \(m\) 个用空格分隔的数字，表示 \(2\) 组每个人的最终情况。

每个情况用一个数字表示，遗憾离场为 \(0\) ，在场但无金条为 \(1\) ，得到金条为 \(2\)。

数据范围

\(1 \le n, m \le 1000, k \le n * m\)

样例输入1

 2 1 1 1 0

样例输出1

 2 1
 1

样例输入2

 2 1 1 1 1 
 2 1

样例输出2

 0 1
 2

样例输入3

 2 2 1 1 1 
 2 2

样例输出3

 0 1
 1 2

题解

Code

T4

题目描述

阿明是一名推销员，他奉命到螺丝街推销他们公司的产品。螺丝街是一条死胡同，出口与入口是同一
个，街道的一侧是围墙，另一侧是住户。螺丝街一共有 \(N\) 家住户，第 \(i\) 家住户到入口的距离为 \(S_i\) 米。由
于同一栋房子里可以有多家住户，所以可能有多家住户与入口的距离相等。阿明会从入口进入，依次向
螺丝街的 \(X\) 家住户推销产品，然后再原路走出去。
阿明每走 \(1\) 米就会积累 \(1\) 点疲劳值，向第 \(i\) 家住户推销产品会积累 \(A_i\) 点疲劳值。阿明是偷懒狂，他想知
道，对于不同的 \(X\) ，在不走多余的路的前提下，他最少可以积累多少点疲劳值。

输入格式

第一行有一个正整数 \(N\) ，表示螺丝街住户的数量。
接下来的一行有 \(N\) 个正整数，其中第 \(i\) 个整数 \(S_i\) 表示第 \(i\) 家住户到入口的距离。数据保证:

$ 1 \le S_1 \le S_2 \le ... \le S_m < 10^8$

接下来的一行有 \(N\) 个正整数，其中第 \(i\) 个整数 \(A_i\) 表示向第 \(i\) 户住户推销产品会积累的疲劳值。数据保证 \(A_i < 1000\)

输出格式

输出 \(N\) 行，每行一个正整数，第 \(i\) 行整数表示当 \(X = i\) 时，阿明最少积累的疲劳值。

数据范围

$ 1 \le N \le 100000, 1 \le A_i < 1000$

样例输入1

 5
 1 2 3 4 5
 1 2 3 4 5

样例输出1

 3
 7
 12
 18
 25

样例输入2

 5
 1 2 2 4 5
 5 4 3 4 1

样例输出2

 7 
 11
 16
 22
 27

题解

Code

Day 12

T1 knapsack

题目描述

义卖活动中一共有 \(n\) 种物品，第 \(i\) 种物品的价值量为 \(v_i\)，价格为 \(w_i\)。（注意价值量和价格是不同的）
你用预知未来的能力得知会有 \(q\) 个人前来买东西，第 \(i\) 个人会带着 \(m_i\) 块钱，且只会购买编号为 \([l_i, r_i]\) 中的物品。第 \(i\) 个人选择的购买物品的方案满足以下条件：

1. 每种物品最多只能买一个
2. 购买的物品的价格总和不能超过 mi。
3. 购买的物品的价值量总和是所有方案中最大的。

你想知道对于每一位买家 \(i\)，是否有合法的选择方案。如果有，你还想知道他购买的物品的价值量总和以及购买物品的方案数（两种方案不同当且仅当存在一种物品 \(x\)，在其中一种方案中购买了一个，而在另一种方案中没有购买）。（方案数只需要输出模 \(998244353\) 后的结果即可，如果没有合法方案输出 0 0）

输入格式

第一行一个正整数 \(n\)，表示物品的种类数。
接下来 \(n\) 行，第 \(i\) 行三个正整数 \(v_i\)，\(w_i\)，表示第 \(i\) 种物品的信息。
接下来一行一个正整数 \(q\)，表示买家人数。
接下来 \(q\) 行，每行三个正整数 \(l_i, r_i, m_i\) 表示一位买家的信息。

输出格式

\(q\) 行，第 \(i\) 行两个正整数依次表示第 \(i\) 个人的最大值和取模后的最大值方案数。（如果没有合法方案输出 0 0，占一行，用空格隔开）

数据范围

\(1 \le l_i \le r_i \le n \le 20000, 1 \le q \le 100000, 1 \le m_i \le 500\)

\(1 \le w_i \le 500, 1 \le v_i \le 10^6\)

样例输入

 5
 1 5
 8 1
 1 6
 4 10
 10 2
 5
 2 4 1
 1 3 6
 1 5 10
 2 3 5
 2 4 4

样例输出

 8 1
 9 1
 19 2
 8 1
 8 1

题解

Code

T2 ancestor

题目描述

你的外星笔友 ∝‡ℑ 给你寄来了一封信请你帮它解决一个问题：
∝‡ℑ 的家族通过无性繁殖来繁衍后代，如果 \(x\) 通过无性繁殖产生了 \(y\)，我们不妨称 \(x\) 是 \(y\) 的父亲，显然如果一个成员有父亲，那么父亲是唯一的。我们称 \(x\) 是 \(y\) 的祖先，当且仅当

\(x = y\)，或 \(x\) 是 \(y\) 父亲的祖先。

∝‡ℑ 的家族有 \(n\) 个成员，编号为 \(1..n\)，其中编号为 \(1\) 的成员是所有成员的共同祖先。它们住所排成一排，住在从西往东第 \(i\) 个住所的是编号为 \(i\) 的家庭成员。
∝‡ℑ 的家族中编号为 \(i(i > 1)\) 的成员的父亲为编号为 \(p_i\) 的成员。
如果编号为 \(i\) 的成员要去拜访编号为 \(j\) 的祖先，必须要满足以下条件：

1.\(j ≤ i\)。
2. 对于所有的 \(k(j < k ≤ i)\)，都有 \(j\) 是 \(k\) 的祖先。
∝‡ℑ 想知道，对于每个家庭成员，有多少个可以拜访的祖先.

输入格式

第一行一个正整数 \(n\)，表示成员个数，编号为 \(1..n\)
接下来一行 \(n - 1\) 个数，第 \(i\) 个数 \(p_i + 1\) 表示编号为 \(i + 1\) 的成员的父亲。

输出格式

\(n\) 行，第 \(i\) 行一个正整数表示成员 \(i\) 的答案。

数据范围

\(1 \le n \le 2200000\)

样例输入

 5
 1 1 1 4

样例输出

 1
 2
 2
 2
 3

题解

Code

T3 rebuild

题目描述

\(A\) 国有 \(n\) 个城市，编号为 \(1\) 到 \(n\)，\(n\) 个城市由 \(n - 1\) 个传送门连接，每个传送门连接两个城市，第 \(i\) 个传送门连接编号为 \(x_i\) 的城市和编号为 \(y_i\) 的城市，\(x_i\) 和 \(y_i\) 可以通过这个传送门互相到达。保证每个城市可以通过这些传送门到达其他任意一个城市。每个传送门有一个重要程度，第 \(i\) 个传送门的重要程度为 \(z_i\)。

由于干旱少雨、植被破坏、风力侵蚀、流水侵蚀、土壤盐渍化等因素，\(A\) 国原先的传送门面临着老化等问题。\(A\) 国决定要重建一组新的传送门。\(A\) 国的建造方案有以下要求：

1. 新传送门一共建造 \(n - 1\) 个，建造完成后从每个城市可以通过新传送门到达任意一个城市。

2. 每个新传送门的重要程度在 \([1, n - 1]\) 中，且为整数。

3. 对于任意两个城市 \(x\), \(y(x \ne y)\)，从 \(x\) 通过若干新传送门到达 \(y\) 必须要经过的新传送门的最大重要程度和之前（从 \(x\) 通过若干老传送门到达 \(y\) 必须要经过的老传送门的最大重要程度）的相同。

两个建造方案不同当且仅当存在两个城市 \(x\), \(y\)，其中一组方案中有新传送门连接 \(x\),\(y\) 而另一组中没有或者必须要经过的新传送门的最大重要程度不同。

由于你经常往返于城市 \(u\) 和 \(v\)，你想知道对于所有的 \(i(1 ≤ i ≤ n)\)，有多少种重建的合法方案，满足你只通过新传送门从 \(u\) 到 \(v\) 需要经过的最少城市数量为 \(i\)（包含两个 \(u\) 和 \(v\)，如果 \(u = v\) 则最少城市数量一定为 \(1\)）。
由于答案可能很大，所以你只需要输出答案模 \(998244353\) 之后的结果。

输入格式

第一行一个正整数 \(n\)，表示城市个数。

接下来 \(n - 1\) 行，每行三个正整数 $x_i, \(y_i\), \(z_i\) 如题所述，表示第 \(i\) 个传送门的信息。

接下来一行两个整数 \(u, v\)，如题所述。

输出格式

一行 \(n\) 个正整数，第 \(i\) 个整数表示要经过的最少城市数量为 \(i\) 时的方案数模 \(998244353\) 之后的结果。

数据范围

\(1 \le z_i \le n - 1\)
\(a \le x_i, y_i, u, v \le n \le 500\)

样例输入1

 4
 2 1 3
 3 1 2
 4 2 1
 1 2

样例输出1

 0 1 2 1

样例输入2

 6
 3 4 1
 6 5 1
 1 5 2
 5 2 1
 5 3 1
 6 1

样例输出2

 0 125 200 180 96 24

样例输入3

 12
 2 12 1
 8 10 3
 11 8 3
 2 9 1
 4 1 3
 1 7 4
 8 4 3
 1 6 2
 8 12 3
 5 8 5
 9 3 1
 5 10

样例输出3

 0 12800000 19200000 27008000 29100800 24384640 16021632 8264256 3118656 784512 111744 5760

题解

Code

T4 derivative

题目描述

给定 \(n, k, a, b\)
求
$ \sum\limits_{i = 0}^{n} a^i b^{ik}\dbinom{nk}{ik} $

输入格式

一行四个正整数 \(n, k, a, b\)，表示输入的数据。

输出格式

输出答案模上\(998244353\)。

数据范围

\(1 \le n \le 10^12, 1 \le k \le 5*10^4, 1 \le a, b < 998244353\)

样例输入1

 5 2 2 2

样例输出1

 338409

样例输入2

20 3 4 2

样例输出2

957471120

样例输入3

1000000000 2 5 6

样例输出3

827467897

样例输入4

 1000000000 3 18 7

样例输出4

 870071422

样例输入5

 1000000000 99 655 122

样例输出5

 101310168

样例输入6

 1000000000000 50000 124 2424

样例输出6

 584412109

题解

Code

Day 13

T1 shop

题目描述

小 A 的学校附近共有 \(n\) 个商店，在时刻 \(0\) 时，小 A 从校门口出发开始购物。

从校门口走到任意一个商店，或从一个商店走到另一个商店需要 \(1\) 单位时间。

每个商店 \(i\) 有两个参数 $a_i,b_i $,如果小 A 在时刻 \(t\) 到达了商店 \(i\) ，他需要先花费\(a_i * t + b_i\) 的时间排队，再在这家商店买东西。

小 A 想知道，在时刻 \(T +0.5\) 之前他最多能在多少个不同商店买到物品呢？

这里假定只会在走路和排队上消耗时间，购买物品不消耗时间。

输入格式

第一行输入两个正整数依次表示 \(n, T\)。

接下来 \(n\) 行每行两个正整数，第 \(i\) 行输入 \(a_i, b_i\) 。

输出格式

一个非负整数，表示答案。

数据范围

\(1 \le n \le 2 * 10^5, 0 \le a_i, b_i, T \le 10^9\)

样例输入

 3 7
 2 0
 3 2
 0 3

样例输出

 2

题解

Code

T2 teatime

题目描述

作为信国的游客，伊雷娜入境第一件事就是去喝下午茶，在茶点店伊雷娜发现了一个神秘的菜单，一共有\(2n\)道甜品，每一件甜品都被赋予了一个数 \(a_i\) 表示其完美程度。
对于她来说，一个完美的下午被定义为选定两份心仪的甜品 \(x，y\)如果\(a_x + a_y\) 是 \(p\)的倍数，那么就是完美的。

伊雷娜准备在信国停留 \(n\) 天，她希望能够每天都吃到不一样的甜品，且都度过完美的下午。但这并不一定可以完成，不过别忘了她可是灰之魔女，所以可以使用一个单位的魔力将 \(a_i\) 变成 \(a_i * 2\)。

现在她想要使用若干魔力改变甜品，使得存在一种 \(n\) 天的完美下午的甜点方案。请帮帮她计算完成目标所需的最少魔力吧！

输入格式

第一行一个正奇数 \(p\)，对于任意正整数 \(y\)，\((2^y + 1)\) 与 \(p\)互质。

然后第二行一共 \(p - 1\)个非负整数，第 \(j\) 个数表示 \(a_i = j\) 的甜品一个有 \(b_j\)个。
\(2n = \sum b_j\)

输出格式

一个数，表示答案，数据保证有解。

数据范围

\(1 \le p \le 2 * 10^6, b_i \le 10^8\), \(p\)为正奇数，对于任意正整数 \(y\)，$(2^y + 1) 与 \(p\) 互质。
保证答案不超过 long long 类型范围内。

样例输入1

 7
 1 2 0 1 3 1

样例输出1

 1

样例输入2

 2 3
 0 0 0 0 2 6 4 5 0 2 4 5 6 3 6 1 0 5 6 0 1 0

样例输出2

 42

题解

Code

T3 complex

题目描述

GreenDuck 的团队里有很多很多人(有三十万个)，但大部分时候，只有他一个人出题。因此，出题的速度很慢。

小 P 等不了那么久，于是他就去找 GreenDuck。当他进入 GreenDuck 房间时，他发现 GreenDuck 并没有在出题，而是在玩最近很火爆的一款游戏“Chaos Complex”！这让 GreenDuck 很是尴尬。

但 GreenDuck 灵机一动，便根据这款游戏现场编出了一道题。“Chaos Complex”是一款休闲散步类小游戏，它在平面直角坐标系里有 \(n\)个点，其中第 \(i\) 点的坐标为 \((x_i, y_i)\)，而玩家需要画出一个面积最小的矩形来覆盖所有点(可以在边上，也可以在角上)，并且四条边要么平行于 x 轴，要么平行于 y 轴。GreenDuck 便把这道题给了小 P 。

这当然难不倒小 P ，小 P 也立即给出了解答，并嘲笑 GreenDuck 出题太没水平。这让 GreenDuck 很是恼火，于是他说：

“假如这 \(n\) 个点均在集合 \(S\) 中，求出 \(S\)的所有 \(2^n\) 个子集所对应的点的最小矩形的面积之和，答案对 \(998244353\) 取模”。

这下小 P 不会了，并陷入了困惑之中。请你帮助小 P 算出这个结果。

输入格式

第一行一个整数 \(n\)，表示点的个数。

接下来 \(n\) 行，每行两个正整数\(x_i ，y_i\) 表示点的坐标。

输出格式

输出一行一个数字，表示答案对\(998244353\)取模的结果。

数据范围

$ 1 \le n \le 200000, max(x_i, y_i) \le 10^9$

样例输入

 4
 1 1
 1 3
 3 1
 3 3 

样例输出

 28

题解

Code

T4 nuance

题目描述

GreenDuck 认为这套题应该简单点，所以他不打算给这道题编故事了。

这道题中，所有字符串的字符集为 \(\sum \enspace a, b, ..., y, z\)，即所有小写英文字母。

对于一个定义在字符集 \(\sum\) 上的双射 \(f\)，即 \(\forall w \in \sum\) ，\(f(w)\) 的值互不相同且取遍字符集 \(\sum\)，那么，对于一个字符串 \(S \enspace = \enspace a_1a_2...a_k\)，定义它的变换 \(G(S, f)\)为

\(G(S, f) = T = f(a_1)f(a_2)...f(a_k)\)

例如， \(S = abc\)，那么 \(G(S, f)\) 可以是 \(aba(f(a) = a, f(b) = b)\)，可以是 \(gdg(f(a) = g, f(b) = d)\)，但不能是 \(hhh\) (因为这样的话 \(f(a) = f(b) = h\)， \(f\) 不满足双射的定义)，也不能是 \(czy\) ( \(f(a)\) 不能同时为 \(c\) 和 \(y\))。

定义字符串的最小表示为 \(M(S)\)，且 \(M(S) \enspace = \enspace minG(S, f) | for \enspace all \enspace possible \enspace f\)，其中 \(min\)表示取字典序最小的一个字符串。

例如，\(M(abab) \enspace = \enspace abab, M(dcba) \enspace = \enspace abcd, M(babf) \enspace = \enspace abac\) 。

现在有一个长度为 \(n\) 的字符串，有 \(m\) 次询问，它的字符集大小为 \(lim\)，每个字符由 \(1\) 到 \(lim\) 中的一个整数来表示。每次询问会从字符串中选出两段区间\([l_1, r_1]\)和 \([l_2, r_2]\)来组成新的字符串 \(S_{l_1, r_1}\)，\(S_{l_2, r_2}\) 你需要输出 \(M(S_{l_1, r_1})\) 和 \(M(S_{l_2, r_2})\) 的最长公共前缀长度，并比较两个最小表示字符串的大小。

输入格式

第一行两个个整数 \(n\)， \(lim\)，分别表示字符串的长度和字符集大小。

接下来一行共 \(n\) 个整数，第 \(i\) 个数字表示字符串第 \(i\) 个位置的字符。

接下来一行一个整数 \(m\)，表示询问次数。

接下来 \(m\) 行，每行 \(4\) 个正整数 \(l_1, r_1, l_2, r_2\), 相邻两个数用空格隔开。

输出格式

对于每次询问，先输出一个整数表示 \(M(S_{l_1,r_1})\) 和 \(M(S_{l_2, r_2})\)的最长公共前缀长度。

接下来，如果 \(M(S_{l_1, r_1}) \enspace = \enspace M(S_{l_2, r_2})\) ，输出“same”；

如果 \(M(S_{l_1, r_1}) \enspace < \enspace M(S_{l_2, r_2})\)，输出“a”；

否则输出“b”。

其中小于号表示符号前面的字符串，字典序小于后面的字符串。

注意，两个答案之间用一个空格隔开。不要输出双引号。

数据范围

\(1 \le n, m \le 10^5, l_1 \le r_1, l_2 \le r_2, 1 \le lim \le 1000\)

样例输入

 6 3
 1 2 1 2 3 1
 3 
 1 2 5 6
 1 4 2 3
 1 4 3 6

样例输出

 2 same
 2 b
 2 a

题解

Code

Day 14

T1 game

题目描述

这是开始前的故事。
羽入和小梨花在 \(n ∗ m\) 的棋盘上下棋，其中行从 \(1\) 到 \(n\) 标号，列从 \(1\) 到 \(m\) 标号。
棋盘上有两种棋子：车和兵。车每次可以往四个方向走任意格，直到在某个空地停下或
者碰到一个兵把兵吃掉并停下来。兵每次可以往四个方向走一格，要求格子是空地或者是车，
如果是车则将车吃掉。
现在羽入控制车，梨花控制兵，车初始在 \((x_1, y_1)\)，终点在 \((x_2, y_2)\) ，如果车走到了终点
（无论下一步是否存活）则羽入获胜，否则若车被吃了或者羽入在 \(10^{100000}\) 步内无法获胜则梨
花获胜。双方每次只能移动自己的某一个棋子走一步（也可以选择不移动）。
棋盘初始只有一个车，梨花在开始前可以选择在任意非车位置（包括终点）放兵，接着
羽入先手操作车，之后两人轮流操作。
因为羽入除了会啊呜啊呜以外还很聪明，所以梨花想知道自己需要放的最少兵的数量，
使得两人都按照最优策略进行时自己可以获胜，如果无解输出 \(1\)。

输入格式

一行六个数 \(n, m, x_1, y_1, x_2, y_2\)，分别表示棋盘的大小、车的起始位置、终点位置。

输出格式

一行一个数表示答案，无解输出 \(-1\)

数据范围

\(1 \le n, m \le 300\)

样例输入

 2 3 1 1 2 3

样例输出

 1

题解

Code

T2 village

题目描述

给出一个网格图，每个格子有黑白二色，求有多少个子矩形满足将其挖出来后恰好有一
个黑色四连通块且不存在由白色格子组成的空腔。
空腔：某个白色格子在空腔内当且仅当其不能通过上下左右四方向走到边界。

输入格式

第一行两个数 \(n,m\)，表示网格图的大小
接下来 \(n\) 行每行一个长为 \(m\) 的 01 串，表示网格图的颜色情况（0 为白 1 为黑）

输出格式

一行一个数表示答案

数据范围

\(1 \le n, m \le 300\)

样例输入

 4 4
 1111
 1101
 1001
 1111

样例输出

 83

题解

Code

T3 fight

题目描述

给出一条长为 \(n\) 的链，求在上面加上 \(k\) 条边后能形成的经过点序列（不是边）不同的哈密顿路条数
对 \(998244353\) 取模

输入格式

第一行两个数 \(n,k\)，含义如题。

输出格式

一行一个数表示模 \(998244353\) 的答案

数据范围

\(1 \le n \le 200000\)

样例输入

 4 2

样例输出

 22

题解

Code

T4 snow

题目描述

小 P 所在的滑稽王国是一个滑稽图，有 \(n\) 个城市 \(n - 1\) 条道路，其中第 \(i\) 条道路连接
城市 \(x_i, y_i\) 。这真不愧是世界上最滑稽的王国，两两城市居然可以互相到达！(
一场大雪袭来，由于地形原因，不同的道路上的积雪深度是不一样的，第 \(i\) 条道路积了 \(z_i\) 深度的雪。
作为王国的资深铲雪师，小 P 被分配了一个任务，将所有道路上的积雪铲除干净，具体来说，每一次小 P 可以选择一个起点 \(x\) 和终点 \(y\)，然后开着他所向披靡的铲雪车一路从 \(x\) 挖到 \(y\)，使得 \(x\) 到 \(y\) 的简单路径上的积雪深度 \(-1\)。但是由于再厉害的铲雪师也不能凭空召唤铲雪车，小 P 还需要花费 \(w_x + w_y\) 在 \(x, y\) 城市的铲雪车站获得和存放他的铲雪车。
需要注意的是，由于小 P 的铲雪车比较暴躁，所以如果地上没有雪，这辆车甚至会把地皮带走，为了避免给城管缴纳天价罚款，小 P 选择的路径上都一定要有雪。
很不幸的是，小 P 还没有出动，\(q\) 场大雪又接连袭来，让本就滑稽的王国雪上加霜。第 \(i\) 场大雪使得 \(u_i\) 到 \(v_i\) 的简单路径上的积雪增多了 \(d_i\)。
为了规划好自己的钱包，小 P 想知道对于第 \(1\) 场大雪之前以及每一场大雪之后，共 \(q+1\) 个时候出动并将所有道路的雪铲干净最少要花多少钱（注意每一个询问是互相独立的）。

输入格式

第一行两个整数 \(n, q\)
第二行 \(n\) 个整数，第 \(i\) 个表示 \(w_i\)
接下来 \(n - 1\) 行，每一行三个整数 \(x_i, y_i , z_i\)，表示一条道路 \((x_i, y_i, z_i)\)
接下来 \(q\) 行，每一行三个整数 \(u_i, v_i, d_i\)，表示一场大雪。

输出格式

输出 \(q + 1\) 行，第 \(1\) 行表示询问前的答案，第 \(i(i > 1)\) 行表示第 \(i - 1\) 修改之后的答案，

数据范围

\(1 \le n \le 2*10^5, 0 \le q \le 2*10^5, 0 \le z_i, w_i, d_i \le 10^6, x_i \not = y_i\)

样例输入

 5 3
 3 1 1 3 1
 3 4 1
 3 1 2
 3 5 3
 1 2 3
 1 2 2
 2 4 3
 2 3 2

样例输出

 12
 20
 32
 34

题解

Code

Day 15

T1 forging

题目描述

“欢迎啊，老朋友。”
一阵寒暄过后，厂长带他们参观了厂子四周，并给他们讲锻造的流程。
“我们这里的武器分成若干的等级，等级越高武器就越厉害，并且对每一等级的武器都有两种属性值 \(b\) 和 \(c\)，但是我们初始只能花 \(a\) 个金币来生产 \(1\) 把 \(0\) 级剑……”
“所以你们厂子怎么这么垃圾啊，不能一下子就造出来 999 级的武器
吗？”勇者不耐烦的打断了厂长的话。
“别着急，还没开始讲锻造呢……那我们举例你手中有一把 \(x\) 级武器和
一把 \(y\) 级武器 \((y = max(x - 1, 0))\)，我们令锻造附加值 \(k = min(c_x, b_y)\)，则
你有 \({k \over c_x}\) 的概率将两把武器融合成一把 \(x + 1\) 级的武器。”
“……但是，锻造不是一帆风顺的，你同样有 \(1 - {k \over c_x}\) 的概率将两把武器
融合成一把 \(max(x - 1, 0)\) 级的武器……”
勇者听完后暗暗思忖，他知道厂长一定又想借此机会坑骗他的零花钱，于是求助这个村最聪明的智者——你，来告诉他，想要强化出一把 \(n\) 级的
武器，其期望花费为多少？
由于勇者不精通高精度小数，所以你只需要将答案对 998244353

输入格式

第一行两个整数 \(n, a\)，含义如题所示。
为了避免输入量过大，第二行五个整数 \(bx, by, cx, cy, p\)，按照下列代码
来生成 \(b\) 和 \(c\) 数组。

	b[0]=by+1;c[0]=cy+1;
	for(int i=1;i<n;i++){
		b[i]=((long long)b[i-1]*bx+by)%p+1;
		c[i]=((long long)c[i-1]*cx+cy)%p+1;
	}

输出格式

输出一行一个整数，表示期望花费。

数据范围

\(0 \le a \le 10^7, 0 \le bx, by, cx, cy < p < 10^7\)

样例输入1

 0 6432
 4602677 3944535 2618884 6368297 9477531

样例输出1

 6432

样例输入2

 1 3639650
 6136976 5520115 2835750 9072363 9302097

样例输出2

 150643649

样例输入3

 10 2
 2 33 6 66 2333333

样例输出3

 976750710

样例输入4

 200 5708788
 0 0 0 0 1

样例输出4

 696441597

题解

Code

T2 division

题目描述

整除符号为 \(|\)，\(d|n\) 在计算机语言中可被描述为 \(n%d == 0\)。
现有一算式 \(n|x^m - x\)，给定 \(n，m\)，求 \([1, n]\) 以内 \(x\) 解的个数。
解可能很大，输出取模 \(998244353\)。

输入格式

其中 \(n\) 的给定方式是由 \(c\) 个不超过 \(t\) 的质数的乘积给出的，\(c\) 和 \(t\) 的范围会在数据范围中给出。
第一行一个 \(id\) 表示这个数据点的标号。
多组数据，其中第二行一个整数 \(T\) 表示数据组数。
对于每一组数据：
第一行两个整数 \(c\) 和 \(m\)。
第二行 \(c\) 个整数，这些整数都是质数，且两两不同，他们的乘积即为 \(n\)。
由于你可以通过输入求出 \(t\)，输入不再给出。

输出格式

对于每组数据输出一行，表示解的个数。

数据范围

\(1 \le c \le 50, 1 \le t \le 10^4, 1 \le m \le 10^9, 1 \le T \le 10000\)
(tips 当 \(1 \le t \le 10^2 ,1 \le c \le 2, 1 \le m \le 10\) 的时候，\(1 \le T \le 10000\)， 其它情况下 \(1 \le T \le 50\))

样例输入

 0
 1
 2 3
 2 3

样例输出

 6

题解

Code

T3 money

题目描述

南极的企鹅王国大学中生活着 \(n\) 只企鹅，作为 21 世纪的优秀大学生，企鹅们积极响应“大众创业，万众创新”的号召，纷纷创业。但是创业需要资金，企鹅们最近手头比较紧，只能互相借钱。

企鹅的借钱行为是有规律可循的：每只企鹅只会借一次钱，并且只会从一只企鹅那里借钱。借钱关系中不存在环（即不存在类似“金企鹅欠银企
鹅钱，银企鹅欠铜企鹅钱，铜企鹅欠金企鹅钱”这种情况）。

企鹅的还钱行为也是有规律可循的：每只企鹅一旦新获得了一笔钱，就会立刻用这笔钱尽可能偿还自己欠的债务，直到债务偿清或用光这笔钱。它只会使用新获得的这笔钱，至于以前它有没有钱、有多少钱，与还钱行为无关。

企鹅们经常会做美梦。在一只企鹅 A 的梦里，它梦见自己创业成功，一下子获得了 \(+∞\) 元钱，于是（按照上文的还钱规则）它赶快把钱用来还债，接着拿到钱的那只企鹅也赶快把钱用来还债……如此往复，直到所有获得钱的企鹅都完成了还债操作。梦醒之后，它开心地把梦的内容告诉了另外一只企鹅 B，企鹅 B 听了，也很开心，于是它问道：在你的梦里，我获得了多少钱呢？(指 B 去还债之前手里的钱，包括后来用于还债的钱和还债后
B 手里剩下的钱。)

梦毕竟是梦，对实际的欠债情况没有影响。

输入格式

第一行两个整数 \(n\) 和 \(m\)，表示有 \(n\) 只企鹅，\(m\) 个操作。
接下来 \(m\) 行，有两种可能的格式：

• 0 a b c：修改操作，企鹅 \(a\) 向企鹅 \(b\) 借了 \(c\) 元钱。
• 1 a b：查询操作，询问假如 \(a\) 有了 \(+∞\) 元钱，企鹅 \(b\) 会净收入多少钱。
  本题强制在线，也就是说：对于每个操作输入的变量 \(a, b, c\)（如果没有
  \(c\)，那就只有 \(a, b\)）都不是实际的 \(a, b, c\)，想获得实际的 \(a, b, c\) 应当经过以下
  操作：

 a = (a + lastans) % n + 1;
 b = (b + lastans) % n + 1;
 c = (c + lastans) % n + 1;

其中，\(lastans\) 是上一次询问的答案。如果没有上一次询问，\(lastans\) 为 \(0\)。

输出格式

对每个询问操作，输出一行一个数表示答案。

数据范围

$ 1 \le n \le 10^5, 1 \le m \le 10^6, 0 \le a, b, c \le n 且 a \not = b$

样例输入

 5 9
 0 1 2 1
 0 0 1 2
 1 0 1
 1 2 4
 0 2 1 1
 1 2 0
 0 3 1 0
 1 4 2
 1 3 4

样例输出

 3
 2
 0
 1
 0

题解

Code

T4

题目描述

你有个\(n\) 个点 \(m\) 条边的无向图， 每条边都有红蓝两种颜色中的一种， 保证红色的边形成了这个图的一个生成树。

你希望给这些边赋上边权， 保证边权是 \(1 \enspace\)~\(\enspace m\) 的排列， 使得红色边是最小生成树。

希望这些边权形成的序列字典序最小， 也就是比较第一条边的边权再比较第二条边的边权， 依次类推。

输入格式

第一行两个正整数 \(n, m\)

接下来 \(m\) 行， 每行三个整数 \(u_i, v_i, c_i\), \(c_i\) 表示颜色， 其中 \(1\) 表示红色， \(0\) 表示蓝色。

保证没有自环， 可能有重边， 保证 \(c_i = 1\)形成了生成树。

输出格式

一行 \(m\) 个整数， 依次表示每条边的边权。

数据范围

$ 1 \le n, m \le 5 * 10^5, m \ge n - 1$

样例输入

 4 5
 1 2 0
 2 3 1
 3 4 1 
 2 4 0
 1 3 1

样例输出

 3 1 4 5 2

题解

Code

Day 16

T1

题目描述

给定正整数 \(L\) ，对所有满足 \(LCM(a,b) \le L\) 的有序正整数对 \((a, b)\)，求 \(| ax - by|\)的和。这里 \(LCM(a, b)\) 是 \(a, b\) 的最小公倍数。

输入格式

三个正整数 \(L, x, y\)。

输出格式

一个整数

数据范围

\(1 \le L \le 10^6, 1 \le x, y \le 100\)

样例输入1

 3 1 3

样例输出1

 26

样例输入2

 1000 12 15

样例输出2

 97478538

题解

第一眼看上去似乎不是很好处理。
考虑互质的两个数 \(a, b\)
记它们的价值为 \(val_{a, b} \enspace = \enspace |ay - bx| + (a \not = b) |ax - by|\)
再考察任意两个数 \(c, d\).

令他们的最大公因数为 \(k\),显然 \(val_{c, d} \enspace = \enspace val_{c / k, d / k} * k\)
那么此时\(c, d\)互质， 于是我们回到了两数互质的情况。（此时 \(LCM(c, d) \enspace = \enspace LCM(c / k, d / k) * k\))

于是我们枚举每一组互质的数 \(i, j\) 保证 \(i * j \le L\)。
在以此扩展价值的时候， 要保证 \(LCM(i * k, j * k) \le L\)
不难发现每一组互质的\(i, j\)所贡献的价值为 \(val_{i, j} * (1 + 2 + ... \lfloor { L \over LCM(i,j) }\rfloor)\)

Code

#include <bits/stdc++.h>
using namespace std;
#define ll long long
ll L;
ll len, x, y;
ll gcd(ll x,ll y){
	if(y == 0) return x;
	else return gcd(y, x % y);	
}
ll sum(ll x){
	return (1 + x) * x / 2;
}
ll ans = 0;
int main(){
	freopen("a.in", "r", stdin);
	freopen("a.out", "w", stdout);
	scanf("%lld%lld%lld", &L, &x, &y);
	for(int i = 1; i <=  L; i ++){
		ll ed = L / i;
		for(int j = i; j <= ed; j ++){
			if(gcd(i, j) == 1){
				ll base = abs(i * x - j * y) + abs(i * y - j * x) * (i != j);
				ll k = i * j;
				ll o = L / k;
				ll add = base * sum(o);
				ans += add;
			}
		}
	}
	printf("%lld", ans);
	return 0;
}

T2

题目描述

有一棵 \(n\) 个点的树，每条边有边权。有 \(q\) 次询问，每次询问给出 \(u,, v, k\)，记从 \(u\) 到 \(v\) 的简单路径上依次经过的边的边权是 \(b_1, ... b_k\) ，请回答有多少个区间\([l,r]\) 满足 \((b_l,+b_{l + 1}+...+b_r) mod \enspace m \enspace = \enspace k\)。

输入格式

每个测试点有 \(T\) 组数据。两组数据间会换一行。对于每组数据：第一行两个正整数 \(n,m\) 然后 \(n - 1\) 行每行三个正整数 \(u, v, k(0 \le k < m)\) 表示一条树边。接下来一行一个正整数 \(q\) ，紧接着 \(q\) 行每行三个整数 \(u, v, k(0 \le k < m)\)表示一次询问。

输出格式

对每组询问输出一行一个整数。

数据范围

\(1 \le T \le 5, 1 \le n, q \le 10^5, 1 \le m \le 100\)

样例输入

 1
 5 4
 2 1 0
 3 2 3
 4 1 3
 5 4 1
 5
 5 3 0
 5 4 1
 5 2 3
 4 1 1
 4 5 0

样例输出

 3
 1
 2
 0
 0

题解

Code

T3

题目描述

给定序列 \(a_1...a_n\)和 \(b_1 ...b_n\)，有 \(q\) 次询问，每次给定 \(l, r, k(1 \le l \le r \le n)\)，请输出运行以下代码后 \(k\) 的值。

for(int i = l; i <= r; ++i) if(k >= a[i]) k += b[i];

输入格式

本题强制在线，第一行输入三个整数 \(n, q, tp\)，接下来一行 \(n\)个整数 \(a_1 .. a_n\)，接下来一行 \(n\) 个整数 \(b_1 ... b_n\)，接下来 \(q\) 行每行三个正整数 \(l,r, k\)。若 \(tp = 1\)，则真实的 \(k\) 是 \(k \enspace xor (lastans \enspace mod \enspace 998244353)\)，其中 \(lastans\) 是上一次询问的答案。若这是第一次询问，则 \(lastans \enspace = \enspace 0\)。

输出格式

\(q\) 行每行一个整数。

数据范围

\(1 \le n, q \le 3 * 10^5, 0 \le tp \le 1\), 输入的所有数在\([0, 10^9]\).

样例输入

 4 3 0
 3 5 8 6
 1 3 1 2
 1 4 3
 1 4 4
 2 4 3

样例输出

 4
 11
 3

题解

Code

T4

题目描述

给定 \(A_{1...n,1...n}\)，记 \(f(S) \enspace = \enspace \sum_{i \in S, j \in S} A_{i, j}\)，请求有多少个 \(\{1 ... n \}\)的子集 \(S\) 满足 \(f(S)\) 是偶数。答案模 \(998244353\)。

输入格式

每个测试点有 \(T\) 组数据。两组数据间会换一行。对于每组数据：第一行一个正整数 \(n\)，接下来 \(n\) 行每行一个字符串，第 \(i\) 个字符串的第 \(j\) 个字符表示 \(A_{i, j}\)。

输出格式

对每组数据输出一行一个整数。

数据范围

\(1 \le T \le 5, 1 \le n \le 1000, 0 \le A_{i,j} \le 9\)

样例输入

 1
 3
 123
 456
 789

样例输出

 4

题解

Code

Day 17

T1

题目描述

有 \(n\) 个数 \(a_1, a_2, ..., a_n\)， 你需要找到一个集合 \(S\) , 使得 \(S\) 中严格大于 \(S\) 的平均数的数字个数尽量多。输出最多的个数。
注意：这里的集合是可重集， 数字可以重复。

输入格式

第一行一个整数 \(n\)
接下来一行 \(n\) 个整数 \(a_1, a_2, ... a_n\)。

输出格式

一个整数， 表示答案。

样例输入

 5
 1 2 3 4 5

样例输出

 2

题解

考虑把所有数字都放在集合里面。
考虑拿出一个数对于答案的贡献。
发现若拿出目前小于平均数的数， 只会让答案更小。 这很显然。
其次， 拿出大于平均数的数， 那么肯定越大越好， 因为这样平均数小了， 答案更大了。
排序后，从后往前删数字， 每删一次搞一波答案，取最大值。

Code

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 114514;
#define ll long long
int n;
int a[N];
ll sum = 0, res = 0; 
int ans = -1;
int main(){
	freopen("a.in", "r", stdin);
	freopen("a.out", "w", stdout); 
	scanf("%d", &n);
	for(int j = 1; j <= n; j ++)
		scanf("%d", &a[j]), sum += a[j];
	res = n;
	sort(a + 1, a + 1 + n);
	for(int i = n; i >= ans; i --){
		int k = sum / i + 1;
		int pos = lower_bound(a + 1, a + 1 + i, k) - a;
		ans = max(ans, i - pos + 1);
		sum -= a[i];
	}
	printf("%d", ans);		
	return 0;
} 

T2 game

题目描述

LZK 发明一个矩阵游戏，大家一起来玩玩吧，有一个 \(N\) 行 \(M\) 列的矩阵。第一行的数 字是 \(1,2,…M\) ,第二行的数字是 \(M+1,M+2…2*M\) ,以此类推，第 \(N\) 行的数字是 \((N-1)*M+1,(N-1)*M+2…N*M\)。 例如,\(N=3,M=4\) 的矩阵是这样的:

  1  2  3  4
  5  6  7  8
  9 10 11 12

对于身为智慧之神的 LZK 来说,这个矩阵过于无趣.于是他决定改造这个矩阵,改造 会进行\(K\)次,每次改造会将矩阵的某一行或某一列乘上一个数字,你的任务是计算最终这 个矩阵内所有数字的和,输出答案对 \(10^9+7\) 取模。

输入格式

第一行包含三个正整数 \(N、M、K\) 表示矩阵的大小与改造次数。接下来的行,每行会 是如下两种形式之一:
\(R X Y\),表示将矩阵的第 \(X(1 \le X \le N)\) 行变为原来的 \(Y(0 \le Y \le 10^9)\) 倍.
\(S X Y\),表示将矩阵的第 \(X(1 \le X \le M)\) 列变为原来的 \(Y(0 \le Y \le 10^9)\) 倍.

输出格式

输出一行一个整数,表示最终矩阵内所有元素的和对 \(10^9+7\) 取模的结果。

数据范围

\(1 \le N, M \le 1000000, 1 \le K \le 100000\)

样例输入1

 3 4 4 
 R 2 4 
 S 4 1 
 R 3 2 
 R 2 0

样例输出1

 94

样例输入2

 2 4 4
 S 2 0
 S 2 3 
 R 1 5
 S 1 3

样例输出2

 80

题解

本题看上去有些难度，难度在于如何推式子。
根据基本的运算性质可知操作是满足交换率的， 不妨先操作行上的操作
首先用两个数组存储每一行和每一列所乘的数, 若没有乘则为1.
设每一行乘的数依次是 \(k_1, k_2, k_3, ...k_n\)

考虑第 \(i\) 列。
在修改前从上到下的值依次是
\(i, i + m, i + 2*m ... i + (n - 1)*m\)
在行上修改完后变成
\(i * k_1, (i + m) * k_2 ... , (i + (n - 1)) * m * (k_n)\)
根据题意将其加起来， 然后合并同类项得到
\(i *(k_1 + k_2 + ... + k_n) + (1 * k_2 + 2 * k_3 + .. (n - 1) * k_n) * m\)
再乘上第 \(i\) 列乘的数， 就是第 \(i\) 行的值。
答案就是每一行的值加起来。
同时发现这个式子里 除了 \(i\) 以外都是定值， 可以在正确时间复杂度内通过此题

Code

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 1e6 + 114514;
const int Mod = 1e9 + 7; 
int n, m, k;
ll mul_r[N], mul_s[N];
ll sum1 = 0, sum2 = 0;
int main(){
	freopen("game.in", "r", stdin);
	freopen("game.out", "w", stdout);
	scanf("%d%d", &n, &m);
	scanf("%d", &k);
	for(int i = 1; i <= n; i ++)
		mul_r[i] = 1;
	for(int j = 1; j <= m; j ++)
		mul_s[j] = 1;
	while(k --){
		char pos;
		int x, y;
		cin >> pos;
		scanf("%d%d", &x, &y);
		if(pos == 'R'){
			mul_r[x] *= y, mul_r[x] %= Mod;
		}
		else mul_s[x] *= y, mul_s[x] %= Mod;
	}
	for(int i = 1; i <= n; i ++){
		sum1 += mul_r[i], sum1 %= Mod;
		sum2 += mul_r[i] * (i - 1), sum2 %= Mod;
	}
	ll ans = 0;
	for(int j = 1; j <= m; j ++){
		ll a = j;
		ll tmp = 0;
		tmp += a * sum1;
		tmp %= Mod;
		tmp += m * sum2;
		tmp %= Mod;
		tmp *= mul_s[j];
//		cout << j <<":" << tmp << endl;
		ans += tmp;
		ans %= Mod; 
	}
	printf("%lld", ans);
	return 0;
} 
/*
2 4 4 
S 2 0 
S 2 3 
R 1 5 
S 1 3
*/

T3 jump

题目描述

跳房子，是一种世界性的儿童游戏，也是中国民间传统的体育游戏之一。 跳房子是在 \(N\) 个格子上进行的，CYJ 对游戏进行了改进，该成了跳棋盘，改进后的游戏 是在一个 \(N\) 行 \(M\) 列的棋盘上进行，并规定从第一行往上可以走到最后一行，第一列往左 可以走到最后一列，反之亦然。每个格子上有一个数字。

在这个棋盘左上角(1,1)放置着一枚棋子。每次棋子会走到右、右上和右下三个方向格 子中对应上数字最大一个。即任意时刻棋子都只有一种走法，不存在多个格子同时满足 条件。 现在有两种操作：

\(move k\) 将棋子前进 \(k\) 步

\(change a b e\) 将第 \(a\) 行第 \(b\) 列格子上的数字修改为 \(e\)。

请对于每一个 \(move\) 操作输出棋子移动完毕后所处的位置。

输入格式

第一行包含两个正整数 \(N,M(3 \le N,M \le 2000)\) ，表示棋盘的大小。
接下来 \(N\) 行，每行 \(M\) 个整数，依次表示每个格子中的数字 \(a[i,j](1 \le a[i,j] \le 10^9)\) 。
接下来一行包含一个正整数 \(Q(1\le Q \le 5000)\)，表示操作次数。
接下来 \(m\) 行，每行一个操作，其中 \(1 \le a \le N,1 \le b \le M,1 \le k,e \le 10^9\)

输出格式

对于每个 \(move\) 操作，输出一行两个正整数 \(x,y\)，即棋子所处的行号和列号。

数据范围

\(3 \le N,M \le 2000，1 \le Q \le 5000，1 \le e,k \le 10^9\)

样例输入

 4 4 
 1 2 9 3 
 3 5 4 8 
 4 3 2 7 
 5 8 1 6 
 4
 move 1 
 move 1 
 change 1 4 100 
 move 1

样例输出

 4 2
 1 3
 1 4

题解

Code

T4 sequence

题目描述

Lxy 养了 \(N\) 头奶牛，他把 \(N\) 头奶牛用 \(1...N\) 编号，第 \(i\) 头奶牛编号为 \(i\)。为了让奶牛 多产奶，每天早上他都会让奶牛们排成一排做早操。奶牛们是随机排列的。在奶牛排列 中，如果一段区间 \([L,R]\) 中的数从小到大排列后是连续的，他认为这段区间是优美的。 比如奶牛排列为：\((3, 1, 7, 5, 6, 4, 2)\) ，区间 \([3,6]\) 是优美的，它包含 \(4,5,6,7\) 连续 的四个数，而区间 \([1,3]\) 是不优美的。Lxy 的问题是：对于给定的一个区间 \([L,R] （1 \le L \le R \le N)\) , 他想知道，包含区间 \([L,R]\) 的最短优美区间，比如区间 \([1,3]\) 的最短优 美区间是 \([1,7]\)。

输入格式

第一行为一个整数 \(N\)，表示奶牛的个数。
第二行为 \(1\) 到 \(N\) 的一个排列，表示奶牛的队伍。
第三行为一个整数 \(M\)，表示有 \(M\) 个询问。
后面有 \(M\) 行，每行有两个整数 \(L,R\) 表示询问区间。

输出格式

输出为 \(M\) 行，每行两个整数，表示包含询问区间的最短优美区间。

数据范围

\(1 \le N, M \le 100000\)

样例输入1

 7
 3 1 7 5 6 4 2
 3
 3 6
 7 7
 1 3

样例输出1

 3 6
 7 7
 1 7

样例输入2

 10
 2 1 4 3 5 6 7 10 8 9 
 5
 2 3 
 3 7 
 4 7 
 4 8 
 7 8

样例输出2

 1 4
 3 7
 3 7 
 3 10 
 7 10

题解

Code

Day 18

T1 rule

题目描述

数据由 \(n\) 个整数组成，第 \(i\) 个数为 \(a_i\)。设 \(a[l : r]\) 表示可重集 \(a_l, a_{l + 1}, ... a_r\)，\(f(S)\) 表示可重集 \(S\) 中所有数去掉最大值和最小值之后的和，若有多个最大值或多个最小值，只去掉一个。求：
\(\sum\limits_{1 \le l \le r \le n, r - l + 1 \ge 3} f(a[l : r])\) 的值， 答案对 \(2^{32}\) 取模

输入格式

第一行一个正整数 \(n\) ，表示序列 \(a\) 的长度。

第二行 \(n\) 个非负整数，表示序列 \(a\)。

输出格式

一行一个整数，表示答案对 \(2{32}\) 取模后的结果。

数据范围

\(3 \le n \le 10^6, 0 \le a_i \le 10^9\)

样例输入1

 3
 0 1 2

样例输出1

 1

样例输入2

 5
 4 2 1 4 3

样例输出2

 27

题解

Code

T2 compose

题目描述

给定两个由大小写字母和数字组成的字符串 \(s, t\) ，定义一个字符串是优美的，当且仅当存在一个正整数 \(k\)，使得所有大小写字母和数字在该字符串中的出现次数恰好为在 \(t\) 中的出现次数的 \(k\) 倍，求 \(s\) 的子串中，有多少子串是优美的。

输入格式

第一行两个正整数 \(n，m\) 分别表示字符串 \(s\) 和 \(t\) 的长度。

第二行一个长度为 \(n\) 的字符串 \(s\)。

第三行一个长度为 \(m\)的字符串 \(t\)。

输出格式

一行一个整数，表示答案。

数据范围

\(1 \le m \le n \le 10^7\)

样例输入1

 5 2
 ababa
 ab

样例输出1

 6

样例输入2

 10 2
 aaabaaaaaa
 aa

样例输出2

 11

样例输入3

 10 4
 aBa0aB0aaB

样例输出3

 0aaB

题解

Code

T3 track

题目描述

你需要提供起点的坐标和 \(n\) 个拐点的坐标，坐标必须是 \(n\) 到 \(10^3\) 之间的整数（含 \(0\) 和 \(10^3\) ），且起点和所有拐点共 \(n + 1\) 个点的坐标不能重复，最后设计出的赛道是连接起点和 \(1\) 号拐点，对于 \(i \in [1, n - 1]\) ，连接 \(i\) 号拐点和 \(i + 1\) 号拐点，然后再连接 \(n\)号拐点和起点后得到的图形，除了端点处外，不允许有线段相交。若有多种方案，提供任意一种即可。可结合样例理解题目意思。

如果满足主办方要求的赛道不可能被设计出来，输出 \(-1\)。

输入格式

本题采用自定义校验器（special judge）评测。

本题有多组数据。

第一行一个正整数 \(T\)，表示数据组数。

对于每组数据：

第一行一个整数 \(n\)。

第二行一个仅由 \(L\) 和 \(R\) 组成的长度为 \(n\) 的字符串。

输出格式

对于每组数据：

若无解，输出 \(-1\)。

否则，第一行两个整数分别表示起点的横纵坐标。

接下来 \(n\) 行每行两个整数，第 \(i\) 行表示第 \(i\) 个拐点的横纵坐标。

数据范围

\(T = 20, 1 \le n \le 10^3\)

样例输入

 5
 3
 RRR
 4
 LRLR
 4
 LLLL
 2
 RR
 9
 RLRRRLRRR

样例输出

 0 0
 0 1
 1 1
 1 0
 -1
 1 1
 1 2
 0 2
 0 0
 1 0
 -1
 2 1
 1 1
 1 2
 0 2
 0 3
 2 3
 2 2
 3 2
 3 0
 2 0

题解

Code

T4 travel

题目描述

共有 \(n\) 个可到达的不同的时空，在高维的视角下排成一行，从左至右依次编号为 \(1\) 至 \(n\)。

现阶段共有两种手段可以实现时空穿梭。每穿梭一次，需要耗费 \(1\) 的代价。

手段一仅限两个相邻的时空之间，但由于一些未知原因，有部分相邻的时空之间无法穿梭，具体情况可用一个长度为 \(n - 1\) 的 \(01\) 串表示，时空 \(i\) 和时空 \(i + 1\) 可以通过手段一互相穿梭，当且仅当该串的第 \(i\) 位为 \(1\)。

手段二仅限两个同组的时空之间。每个时空都属于一个组，同组之间的时空存在一些特定的联系，同组的任意两个时空之间都可以互相穿梭。每个时空所属的组可以用一个长度为 \(n\) 的仅由小写字母组成的字符串表示，两个时空 \(i, j\)属于同一组，当且仅当字符串第 \(i\) 个字母与第 \(j\) 个字母相同。

对于所有不同的满足 \(1 \le u < v \le n\) 的正整数对 \((u, v)\) ，从时空 \(u\) 穿梭到时空 \(v\) 所需的最小代价之和是多少。

输入格式

第一行两个正整数 \(n,m\)，分别表示可到达时空个数和时空组数。

第二行一个长度为 \(n\) 的仅由前 \(m\) 种小写字母组成的字符串，表示每个时空所属的组。

第三行一个长度为 \(n - 1\) 的 \(01\) 串，表示每对相邻的时空之间是否能互相穿梭。

输出格式

一行一个整数，表示答案。

数据范围

\(1 \le n \le 2 * 10^6, 1 \le m \le 18\) 保证从每个时空出发都能到达任意一个时空。

样例输入1

 3 2
 aab
 01

样例输出1

 4

样例输入2

 6 3
 abcbba
 11011

样例输出2

 24

题解

Code

Day 19

T1 rotate

题目描述

ZYL有 \(N\) 张牌编号分别为 \(1, 2，……，N\) 。他把这 \(N\) 张牌打乱排成一排，然后他要做一次旋 转使得旋转后固定点尽可能多。如果第 \(i\) 个位置的牌的编号为\(i\)，我们就称之为固定点。 旋转可以被认为是将其中的一个子段旋转180度，这意味着子段的第一张牌和最后一张 牌交换位置，以及第二张牌和倒数第二张牌交换位置，等等。写一个程序，找到旋转子 段（子段长度可以为\(1\)）。

输入格式

第一行包含一个整数 \(N (1 \le N \le 100 000)\)。
第二行有 \(N\) 个数，第i个数表示旋转之前第 \(i\) 个位置的牌的编号。

输出格式

找到固定点最多的旋转所选的子段，输出旋转之后固定点的个数。

数据范围

\(1 \le N \le 100000\)

样例输入1

 4
 3 2 1 4

样例输出1

 4

样例输入2

 2
 1 2

样例输出2

 2

题解

Code

T2 cell

题目描述

CYJ想找到他的小伙伴FPJ，.CYJ和FPJ现在位于一个房间里,这个房间的布置可以看 成一个N行M列的矩阵,矩阵内的每一个元素会是下列情况中的一种:

1. 障碍区域—这里有一堵墙(用‘#’表示).
2. 这是CYJ最开始在的区域(用‘C’表示).
3. 这是FPJ在的区域(用‘F’表示).
4. 空区域(用‘.’表示).

CYJ携带了一个所谓传送枪的东西,这是一把可以创造传送门的枪械,在每一次行动 中,他可以选择下列操作中的一项:

1. 移向一个相邻的格子中(上,下,左,右,不能移到墙在的格子里).这个操作要 消耗一个单位的时间.
2. 转向一个墙(不需要相邻,只需面向即可),向其发射传送门,传送门会留在墙 内面向你的地方(至多只能同时存在两扇传送门)，若墙上已经有两扇传送 门，而你发射了第三扇,那么最初发射的那一扇会消失。同时,你无法在一个 位置制造两扇传送门（这个操作不会耗费时间）。
3. 如果他与一块墙壁相邻且面前有一扇传送门,那么他可以移动到另一扇传送 门前方的格子。这个操作会耗费一个单位的时间. CYJ想要知道自己最少需要多少时间才能够从起点(‘C’)到达终点(‘F’).
   请注意:我们保证地图边缘会是一圈墙壁且一定存在‘C’,‘F’.

输入格式

第一行输入两个正整数 \(N\) 和 \(M\) ,\((4 \le N,M \le 500)\) .表示地图大小。
接下来的 \(N\) 行每行一个长度为M的字符串.表示地形

输出格式

你需要输出最少的到达终点的时间,如果不能到达请输出 ”no”。

数据范围

\(4 \le N, M \le 500\)

样例输入1

 4 4 
 #### 
 #.F#
 #C.#
 ####

样例输出1

 2

样例输入2

 6 8 
 ######## 
 #.##..F# 
 #C.##..# 
 #..#...# 
 #.....## 
 ########

样例输出2

 4

样例输入3

 4 5
 ##### 
 #C#.# 
 ###F# 
 #####

样例输出3

 no

题解

Code

T3 column

题目描述

WTH获得了一个柱状图,这个柱状图一共有 \(N\) 个柱子,最开始第 \(i\) 柱子的高 度为 \(x_i\) ,他现在要将这个柱状图排成一个屋顶的形状,屋顶的定义如下:

1. 屋顶存在一个最高的柱子,假设为i,最终高度为 \(h_i\) .它是所有柱子之中最 高的.
2. 第j根柱子的高度为 \(h_j=h_i-|i-j|\) ,但这个高度必须大于 \(0\) ,否则就是不合法的.

WTH可以对一个柱子做的操作只有将其高度加一或减一, WTH正忙着享受自 己的人赢生活于是他将把这个柱状图变成屋顶的任务交给了你.你需要求 出最少进行多少次操作才能够把这个柱状图变成一个屋顶形状

输入格式

第一行包含一个正整数 \(N(1 \le N \le 100 000)\).
第二行包含 \(N\) 个用空格隔开的正整数,表示 \(x_i\),含义如题面。

输出格式

输出最少进行多少个操作才能够把这个柱状图变成屋顶的形状。

数据范围

\(1 \le N \le 100000, 1 \le h_i \le 10^9\)

样例输入1

 4
 1 1 2 3

样例输出1

 3

样例输入2

 5
 4 5 7 2 2 

样例输出2

 4

题解

Code

学习清单

prufer
树的同