NOIP 备考日记 Day3
三角
\(ZGY\) 有一个三角,就像下面这样(每一个点都有一个权值)。
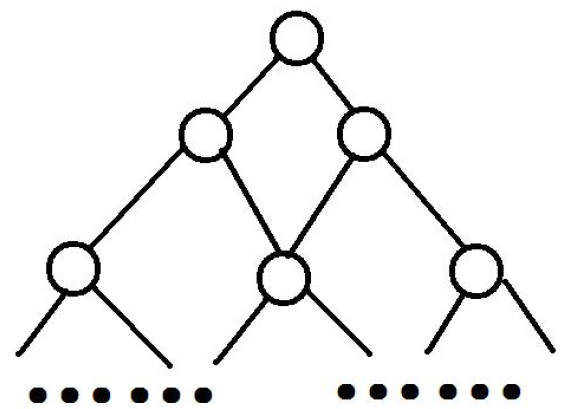
第 \(1\) 层有 \(1\) 个,第 \(2\) 层有 \(2\) 个,第 \(i\) 层有 \(i\) 个。
这个三角一共有 \(n\) 层,\(ZGY\) 每次可以从第 \(i\) 层的第 \(j\) 个走到第 \(i + 1\) 层的第 \(j\) 个或是第 \(j + 1\) 个,直到走到第 \(n\) 层。从第 \(1\) 层走到第 \(n\) 层的一种方案成为一条路径,路径的权值为路径上点权值之和。
现在 \(ZGY\) 想知道,权值前 \(k\) 大的路径(存在多个正确答案)。
输入格式
第一行,两个整数 \(n, k\) 表示三角一共有 \(n\) 层,\(ZGY\) 想知道权值前k 大的路径。
接下来 \(n\) 行:
其中第 \(i\) 行包含 \(i\) 个整数,其中第 \(j\) 个整数 \(W_{ij}\) 表示第 \(i\) 层第 \(j\) 个点权值为 \(W_{ij}\)。
输出格式
输出数据包含 \(k\) 行,每行表示一条路径包含一个由 \(“L”\) 和 \(“R”\) 组成的字符串,长度为 \(n - 1\) 其中第 \(i\) 个字符表示在第 \(i\) 层时向下一层走的方向。
假设当前在第 \(i\) 行第 \(j\) 个点,如果为 \(“L”\) 则走向第 \(i + 1\) 行第 \(j\) 个点,如果为 \(“R”\) 则走向第 \(i + 1\) 行第 \(j + 1\) 个点。
解析
这道题竟然是直接剪枝硬搜。
我们先预处理出当前点到最后一层的最短路径,以及第 \(k\) 长的路径长度。
我们在搜索的过程中记录之前的路径长度,如果之前的路径长度,加上当前点到最后一层最长的路径长度比第 \(k\) 长的路径长度短,那么继续搜下去肯定搜不到最优解。
然后搜到 \(k\) 条之后直接返回。
输出方案拿一个数组记录之前的选择就好了。
注意输出方案的时候有一个小细节。
如果等于第某个前 \(k\) 长的路径长度的某条路径不止一个的话,可能会先输出多个这样的路径导致比他大的路径被占用,所以我们要找完之后排序。
代码
C++锦标赛
题目描述
\(ZGY\) 报名参加了 \(C++\) 锦标赛,在这个比赛中前 \(K\) 名可以获得一本 \(《C++ Primer》\),当然 \(ZGY\) 也想要一本。
这个比赛已经有 \(n\) 个人参加,并且互相之间已经进行了比赛,每一个人都有一个得分,用于最后排名。
\(ZGY\) 作为第 \(n + 1\) 个参赛者,需要与之前的每一个人打一场比赛,当然 \(ZGY\)最开始的得分等于 \(0\)。
对于每场比赛,有两个人参加,不会存在平局,胜者得分增加 \(1\),败者得分不变。
最后按照得分从高到低来排名,假设有人与ZGY 最终得分相同,那么如果那个人曾经输给了 \(ZGY\) 就会排在 \(ZGY\) 后面,否则会排在 \(ZGY\) 的前面。
如果 \(ZGY\) 赢了某个人,就需要消耗相应的 \(RP\) 值,现在 \(ZGY\) 可以决定赢那些人,所以 \(ZGY\) 想知道最少需要消耗多少 \(RP\) 值才能够获得一本 \(《C++ Primer》\)。
输入格式
本题包含多组数据,第一行读入一个整数 \(T\) 表示数据组数
对于每一组数据
第一行,包含两个整数 \(n, k\) 表示在 \(ZGY\) 之前已经有n 个人参加比赛,前k 名可以获得 \(《C++ Primer》\)。
接下来 \(n\) 行,每行包含两个整数 \(p_i\) 和 \(e_i\) 表示第 \(i\) 个人已经获得的得分和赢第 \(i\) 个人所需要花费的 \(RP\)(注意在 \(ZGY\) 来之前这 \(n\) 个人的比赛得分不一定满足上述计分规则)
输出格式
对于每一组数据,输出一个整数,表示最少需要花费的RP,如果无论如何也无法进入前 \(K\) 名,则输出 \(-1\)。
解析

直接贺题解,就是越贪分越高。
写这道题的时候心态炸了,所以码特别丑,建议不要像我一样用堆排,快排更快更方便。
代码
#include<cstdio>
#include<cctype>
#include<cstring>
#include<queue>
#include<algorithm>
using namespace std;
typedef long long LL;
const int N = 2500;
int t, n, k, l, r, score, tot; LL ans = 0;
priority_queue < int > q;
struct data {
int w, c;
bool operator < (const data &x) const {
if(w == x.w) return c < x.c;
return w < x.w;
}
}a[N];
inline void read(int &x) {
x = 0; int c = getchar();
for(; !isdigit(c); c = getchar());
for(; isdigit(c); c = getchar())
x = x * 10 + c - 48;
}
int main() {
freopen("tournament.in", "r", stdin);
freopen("tournament.out", "w", stdout);
read(t);
while(t--) {
read(n), read(k); ans = 1e15;
memset(a, 0, sizeof a);
for(int i = 1; i <= n; i++) read(a[i].w), read(a[i].c);
if(k >= n + 1) { printf("0\n"); continue; }
sort(a + 1, a + 1 + n);
score = a[n - k + 1].w;
if(n < score) { printf("-1\n"); continue; }
if(n >= score + 2) {
ans = 0;
while(!q.empty()) q.pop();
for(int i = 1; i <= n; i++) q.push(-a[i].c);
for(int i = 1; i <= score + 2; i++) ans += -q.top(), q.pop();
}
while(!q.empty()) q.pop();
l = n - k + 1, tot = 0;
for(; ; l--) {
++tot;
if(a[l - 1].w != a[l].w) break;
}
for(r = l; ; r++)
if(a[r].w == score || a[r].w == score + 1) q.push(-a[r].c);
else break;
if(a[r].w != n) r--;
LL res = 0;
for(int i = 1; i <= tot; i++) {
res += -q.top();
q.pop();
}
for(int i = 1; i <= l - 1; i++) q.push(-a[i].c);
for(int i = r + 1; i <= n; i++) q.push(-a[i].c);
if(q.size() >= score - tot + 1) {
for(int i = tot + 1; i <= score + 1; i++) {
res += -q.top();
q.pop();
}
if(res < ans) ans = res;
}
while(!q.empty()) q.pop();
l = n - k + 1, tot = res = 0, r = l + 1;
for(l; l; l--)
if(a[l].w == score || a[l].w == score - 1) q.push(-a[l].c), tot++; else break;
for(r; ; r++)
if(a[r].w == score) q.push(-a[r].c); else break;
for(int i = 1; i <= tot; i++) {
res += -q.top();
q.pop();
}
for(int i = 1; i <= l; i++) q.push(-a[i].c);
for(int i = r; i <= n; i++) q.push(-a[i].c);
if(q.size() >= score - tot) {
for(int i = tot + 1; i <= score; i++) {
res += -q.top();
q.pop();
}
if(res < ans) ans = res;
}
printf("%lld\n", ans);
}
return 0;
ZGY 的早餐
题目描述
\(ZGY\) 每天早上要从宿舍走路到机房,顺便从学校小卖部购买早饭,当然机智的 \(ZGY\) 一定会走最短路。
学校的路可以看成一张无向联通图,图上有 \(n\) 个点,\(m\) 条边,每一个点都有一个唯一的编号 \(1\) ~ \(n\),每一条边有一个边权,表示两个点之间的距离,\(ZGY\) 的宿舍在 \(S\) 点,机房在 \(T\) 点,而小卖部在 \(H\) 点。
现在 \(ZGY\) 想知道从宿舍经过小卖部到达机房的最短距离,不过因为在这个世界上有 \(Q\) 个 \(ZGY\),所以你必须回答 \(Q\) 个问题。
输入格式
第一行包含三个正整数 \(T\), \(n\) , \(m\) 表示这是第 \(T\) 个数据图上有 \(n\) 个点 \(m\) 条边。
接下来 \(m\) 行, 每行有三个整数 \(u, v, w\) 表示点 \(u\) 与 \(v\) 之间有一条长度为 \(w\) 的边(题目保证不存在自环、重边)。
接下来一行,包含一个整数 \(Q\) 表示 \(ZGY\) 的个数。
接下来 \(Q\) 行,每行三个整数 \(S, H, T\) 分别表示宿舍、小卖部、机房所在的点的编号。
输出格式
对于每一个询问 \(Q\),输出一行,表示对于这个询问的答案。

解析
题目贴心的给我们营造了一个良好的数据分治的体验感。
我们必须先走到商店,然后再到机房,每次都是一个独立的最短路问题,所以从宿舍到商店的最短路加上商店到机房的最短路就是总的最短路。
因为多组询问,所以我们要解决的就是如何快速找出全源最短路径,一般有两种算法,Floyd 和 Johnson。
但是显然两种算法都不能解决第二个部分的数据范围。
观察到第二个部分图的特点。
不难发现联通无环图即是一棵树。
所以两个点之间的路径只有唯一一条,这个时候我们树上差分求两点之间的距离就好了。
代码
#include<cstdio>
#include<cctype>
#include<queue>
#include<cstring>
using namespace std;
typedef long long LL;
inline void read(int &x) {
x = 0; int c = getchar();
for(; !isdigit(c); c = getchar());
for(; isdigit(c); c = getchar())
x = x * 10 + c - 48;
}
void write(LL x) {
if(x > 9) write(x / 10);
putchar(x % 10 + '0');
}
namespace lmf {
const int N = 205;
int n, m, q; LL d[N][N];
inline void solve() {
read(n), read(m);
memset(d, 0x3f, sizeof d);
for(int i = 1; i <= n; i++) d[i][i] = 0;
for(int i = 1, x, y, z; i <= m; i++) {
read(x), read(y), read(z);
d[x][y] = d[y][x] = z;
}
for(int k = 1; k <= n; k++)
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
read(q);
for(int i = 1, s, h, t; i <= q; i++) {
read(s), read(h), read(t);
write(d[s][h] + d[h][t]); putchar('\n');
}
}
}
namespace hly {
const int N = 1e5 + 5;
int n, m, k, head[N], nex[N << 2], to[N << 2], w[N << 2], tot = 1;
inline void add(int x, int y, int z) {
nex[++tot] = head[x], to[tot] = y, w[tot] = z, head[x] = tot;
nex[++tot] = head[y], to[tot] = x, w[tot] = z, head[y] = tot;
}
int f[N][20], dep[N]; LL dis[N];
queue < int > q;
inline void bfs() {
q.push(1); dep[1] = 1;
while(!q.empty()) {
int x = q.front(); q.pop();
for(int i = head[x], y; i; i = nex[i]) {
y = to[i];
if(dep[y]) continue;
dep[y] = dep[x] + 1;
dis[y] = dis[x] + w[i];
f[y][0] = x;
for(int j = 1; j < 20; j++)
f[y][j] = f[f[y][j - 1]][j - 1];
q.push(y);
}
}
}
inline void swap(int &x, int &y) { x ^= y ^= x ^= y; }
inline int lca(int x, int y) {
if(dep[x] > dep[y]) swap(x, y);
for(int i = 19; ~i; i--)
if(dep[f[y][i]] >= dep[x]) y = f[y][i];
if(x == y) return x;
for(int i = 19; ~i; i--)
if(f[x][i] != f[y][i]) x = f[x][i], y = f[y][i];
return f[x][0];
}
inline LL get(int x, int y) { return dis[x] + dis[y] - dis[lca(x, y)] * 2; }
inline void solve() {
read(n), read(m);
for(int i = 1, x, y, z; i <= m; i++) {
read(x), read(y), read(z);
add(x, y, z);
}
bfs();
read(k);
for(int i = 1, s, h, t; i <= k; i++) {
read(s), read(h), read(t);
write(get(s, h) + get(h, t)); putchar('\n');
}
}
}
int t;
int main() {
freopen("mindis.in", "r", stdin);
freopen("mindis.out", "w", stdout);
read(t);
if(t <= 6) lmf :: solve();
else hly :: solve();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号