[ZJOI2013] 话旧

题面

[ZJOI2013]话旧

题解

我们知道具有一定性质的函数 \(f\) 图像上的 \(k\) 个点，问满足条件的 \(f\) 有多少个。
性质：

1. 函数 极小值 为 \(0\)，意味着图像的某一段如果下降，必须下降到 \(x\) 轴，且不穿过 \(x\) 轴。
2. 函数斜率为 \(1\) 或 \(-1\)。

然后我们考虑两个点之间的函数图像有哪些可能。
对于左边的点的横纵坐标我们称为 \(x_1, y_1\)，右边的点我们称作 \(x_2, y_2\)。
设 \(f[i][0/1]\) 表示到第 \(i\) 个点为止且第 \(i\) 个点处于上升 / 下降的趋势的方案数。
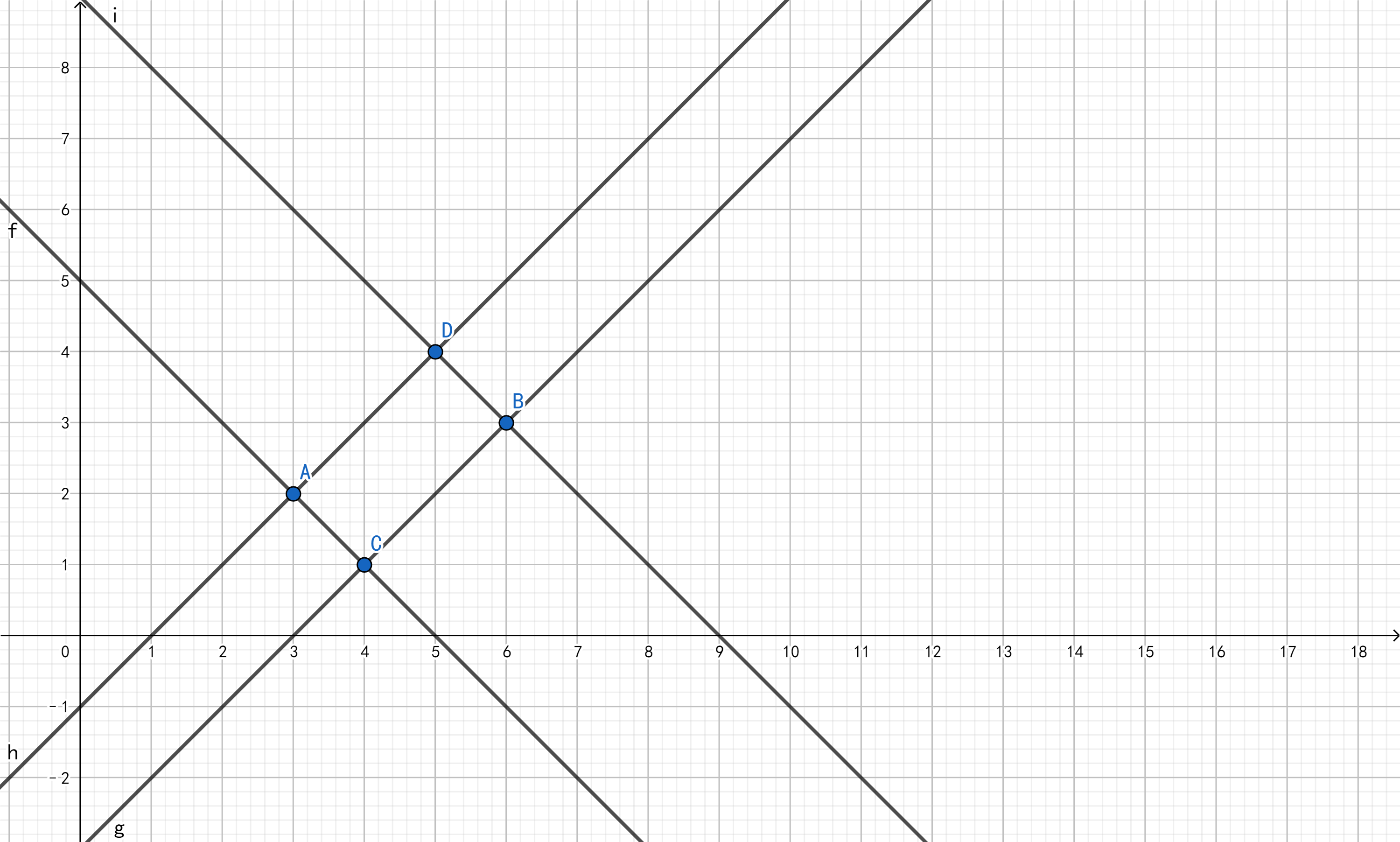
如下图：

1. 假如我们知道的是形如 \(A,B\) 两点的坐标，根据性质 \(1,2\)，当 \(C\) 在 \(x\) 轴上方时，\(A,B\) 之间符合条件的图像只能是折线 \(ADB\)，\(C\) 在 \(x\) 轴或其下方时的情况在下文。显然 \(B\) 是下降点，当 \(A\) 不在 \(x\) 轴上时， 根据性质 \(1\)，\(A\) 只能是上升点，如果 \(A\) 在 \(x\) 轴上，则 \(A\) 可能是上升点，也可能是下降点，要特判 \(y_1\) 是否等于 \(0\)。
2. 假如我们知道的是形如 \(A,D\) 两点处于同一条上升线段上的两点，那么就直接判断 \(AD\) 的斜率是否为 \(1\)，同样需要判断前一个点是否在 \(x\) 轴上。
3. 假如我们知道的是形如 \(D,B\) 两点处于同一条下降线段上的两点，那么就直接判断 \(DB\) 的斜率是否为 \(-1\)，前一个点上升下降无所谓。

这三种情况对应的状态转移方程如下：

if(a[i - 1].x - a[i].x == a[i - 1].y - a[i].y) {//情况 2
  f[i][0] = (f[i][0] + f[i - 1][0]) % mod;
  if(a[i - 1].y == 0) f[i][0] = (f[i][0] + f[i - 1][1]) % mod;
}
else if(a[i - 1].x - a[i].x == a[i].y - a[i - 1].y) 情况 3
  f[i][1] = (f[i][1] + f[i - 1][0] + f[i - 1][1]) % mod;
else if(len < 0) { 情况 1
  f[i][1] = (f[i][1] + f[i - 1][0]) % mod;
  if(a[i - 1].y == 0) f[i][1] = (f[i][1] + f[i - 1][1]) % mod;
}

当 \(C\) 点在 \(x\) 轴或其下方时。
然后不想画图了，太难画了，参照一下 renfei147 大佬的题解。

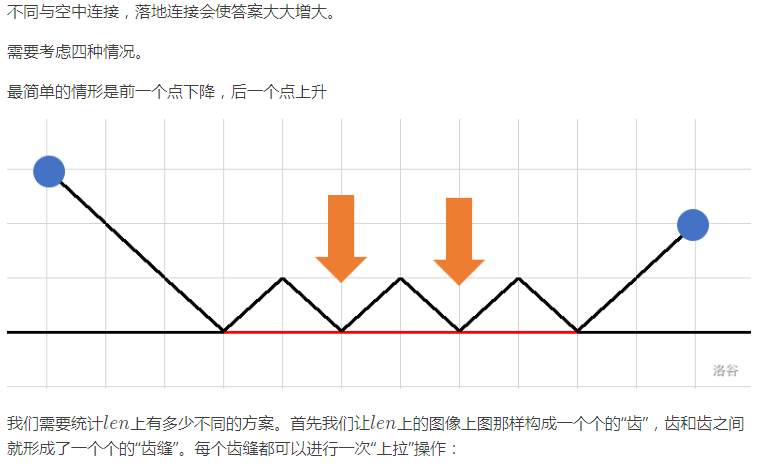
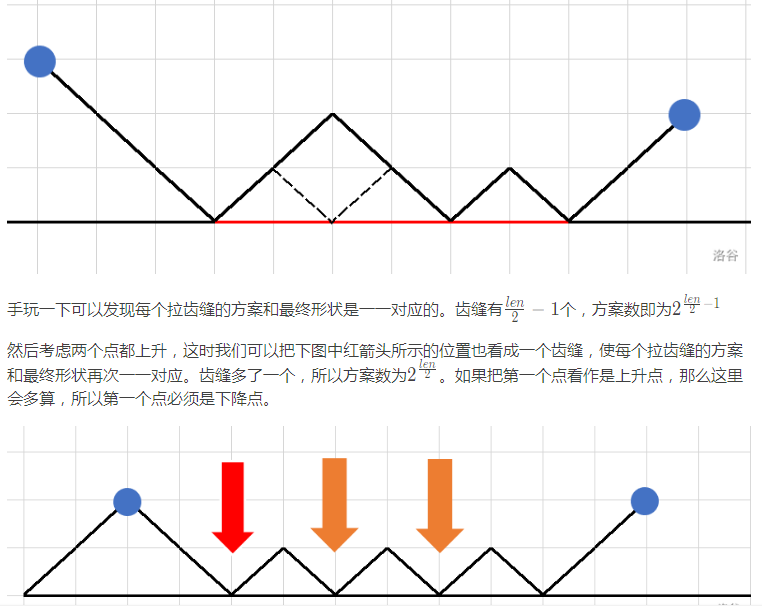
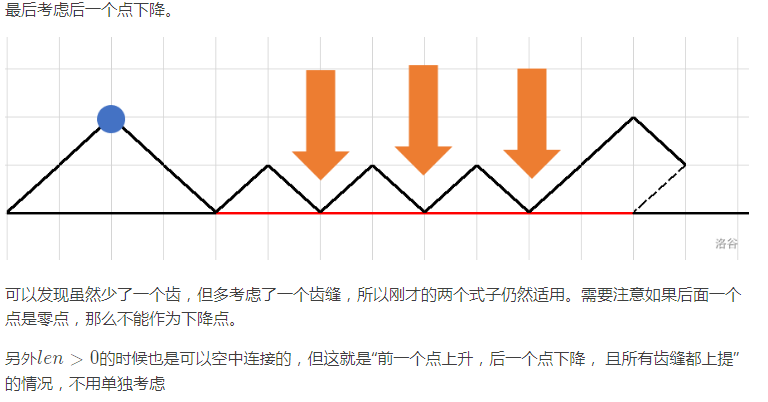
然后找 Max 的方法很简单，根据第一幅图就能看出，每段可能的最大值即为

(a[i].x - a[i - 1].x + a[i].y + a[i - 1].y) >> 1

但要注意判断当前点是否可能是下降点，不然最大值的判断是不成立的。

代码

#include<cstdio>
#include<algorithm>

using namespace std;

const int N = 1e6 + 5, mod = 19940417;

struct data {
	int x, y;
	bool operator < (const data &a) const {
		return x < a.x;
	}
	bool operator == (const data &a) const {
		return (x == a.x) & (y == a.y);
	}
}a[N];

int n, k, f[N][2]; long long Max = 0;

int power(int a, int b) {
	int ans = 1;
	for(; b; b >>= 1, a = 1LL * a * a % mod)
		if(b & 1) ans = 1LL * ans * a % mod;
	return ans;
}

int main() {
	scanf("%d%d", &n, &k);
	for(int i = 1; i <= k; i++) scanf("%d%d", &a[i].x, &a[i].y);
	a[k + 1].x = n;
	sort(a, a + 1 + k + 1);
	k = unique(a, a + 1 + k + 1) - a - 1;
	f[0][1] = 1;
	for(int i = 1; i <= k; i++) {
		int len = a[i].x - a[i - 1].x - a[i].y - a[i - 1].y;
		if(a[i - 1].x - a[i].x == a[i - 1].y - a[i].y) {
			f[i][0] = (f[i][0] + f[i - 1][0]) % mod;
			if(a[i - 1].y == 0) f[i][0] = (f[i][0] + f[i - 1][1]) % mod;
		}
		else if(a[i - 1].x - a[i].x == a[i].y - a[i - 1].y)
			f[i][1] = (f[i][1] + f[i - 1][0] + f[i - 1][1]) % mod;
		else if(len < 0) {
			f[i][1] = (f[i][1] + f[i - 1][0]) % mod;
			if(a[i - 1].y == 0) f[i][1] = (f[i][1] + f[i - 1][1]) % mod;
		}
		else if(len == 0) {
			f[i][1] = (f[i][1] + f[i - 1][0]) % mod;
			if(a[i - 1].y == 0) f[i][1] = (f[i][1] + f[i - 1][1]) % mod;
			f[i][0] = (f[i][0] + f[i - 1][0] + f[i - 1][1]) % mod;
		}
		else {
			int tmp = (2LL * f[i - 1][0] + f[i - 1][1]) % mod * power(2, len / 2 - 1) % mod;//乘二是把多减的 1 加回来
			if(a[i].y > 0) f[i][0] = (f[i][0] + tmp) % mod;
			f[i][1] = (f[i][1] + tmp) % mod;
		}
		if(f[i][1] || a[i].y == 0) Max = max(Max, 1LL * (a[i].x - a[i - 1].x + a[i].y + a[i - 1].y) >> 1);
	}
	printf("%d %lld\n", f[k][1], Max);
	return 0;
}