PTA 1045 快速排序 (25分) 线段树暴力解
题目
著名的快速排序算法里有一个经典的划分过程:我们通常采用某种方法取一个元素作为主元,通过交换,把比主元小的元素放到它的左边,比主元大的元素放到它的右边。 给定划分后的 N 个互不相同的正整数的排列,请问有多少个元素可能是划分前选取的主元?
例如给定 $N = 5$, 排列是1、3、2、4、5。则:
- 1 的左边没有元素,右边的元素都比它大,所以它可能是主元;
- 尽管 3 的左边元素都比它小,但其右边的 2 比它小,所以它不能是主元;
- 尽管 2 的右边元素都比它大,但其左边的 3 比它大,所以它不能是主元;
- 类似原因,4 和 5 都可能是主元。
因此,有 3 个元素可能是主元。
输入格式:
输入在第 1 行中给出一个正整数 N(≤); 第 2 行是空格分隔的 N 个不同的正整数,每个数不超过 1。
输出格式:
在第 1 行中输出有可能是主元的元素个数;在第 2 行中按递增顺序输出这些元素,其间以 1 个空格分隔,行首尾不得有多余空格。
分析:
题意:判断一个数是否符合满足下面的条件:
1、前面的数都小于自己
2、后面的数都大于自己
一开始我的想法是卡一个最大值,一个最小值,一个从前向后遍历,另一个从后向前遍历,标记符合要求的数,最后sort一下就行。复杂度O(2n+mlogm),稳过!
这也太简单了吧,于是突发奇想,我要挑战程序忍耐极限,于是便写了颗线段树模拟暴力解(遍历每个元素,满足元素前面最大值<该元素<元素后面最小值,则储存在答案数组中),时间复杂度O(2nlongn+mlogm),空间复杂度O(4n)。嘿嘿试试看,希望能ac。
代码:

#include<stdio.h> #include<algorithm> using namespace std; int i,j,n; int a[100005]; int num[100005]; struct Tree{ int l,r,maxx,minn; }t[400005]; void built(int i,int l,int r){ t[i].l=l; t[i].r=r; if(l==r){ t[i].maxx=a[l]; t[i].minn=a[l]; return; } int mid=(l+r)/2; built(i*2,l,mid); built(i*2+1,mid+1,r); t[i].maxx=max(t[i*2].maxx,t[i*2+1].maxx); t[i].minn=min(t[i*2].minn,t[i*2+1].minn); } int mi(int i,int l,int r){ if(l==t[i].l && r==t[i].r){ return t[i].minn; } int mid=(t[i].l+t[i].r)/2; if(r<=mid){ return mi(i*2,l,r); } else if(l>mid){ return mi(i*2+1,l,r); } else{ return min(mi(i*2,l,mid),mi(i*2+1,mid+1,r)); } } int ma(int i,int l,int r){ if(l==t[i].l && r==t[i].r){ return t[i].maxx; } int mid=(t[i].l+t[i].r)/2; if(r<=mid){ return ma(i*2,l,r); } else if(l>mid){ return ma(i*2+1,l,r); } else{ return max(ma(i*2,l,mid),ma(i*2+1,mid+1,r)); } } int searchmax(int i,int l,int r){ if(r==0){ return 1; } else{ return ma(1,l,r)<=a[i]; } } int searchmin(int i,int l,int r){ if(l>r){ return 1; } else{ return mi(1,l,r)>=a[i]; } } int main() { int ans=0; scanf("%d",&n); for(i=1;i<=n;i++){ scanf("%d",&a[i]); } built(1,1,n); for(j=1;j<=n;j++){ if(searchmax(j,1,j-1) && searchmin(j,j+1,n)){ num[ans]=a[j]; ans++; } } printf("%d\n",ans); sort(num,num+ans); for(i=0;i<ans-1;i++){ printf("%d ",num[i]); } printf("%d",num[ans-1]); }
结果:第二个测试点WA了,所幸没有TLE,难道还有没有考虑的地方?应该是极端的数,噢噢,傻了,ans=0的时候不就不用输出了吗?特判ans=0时return0结束就行了,啊格式错误,再看了下输出要求,原来要2行,要printf("\n"),坑啊!(还好不是比赛)
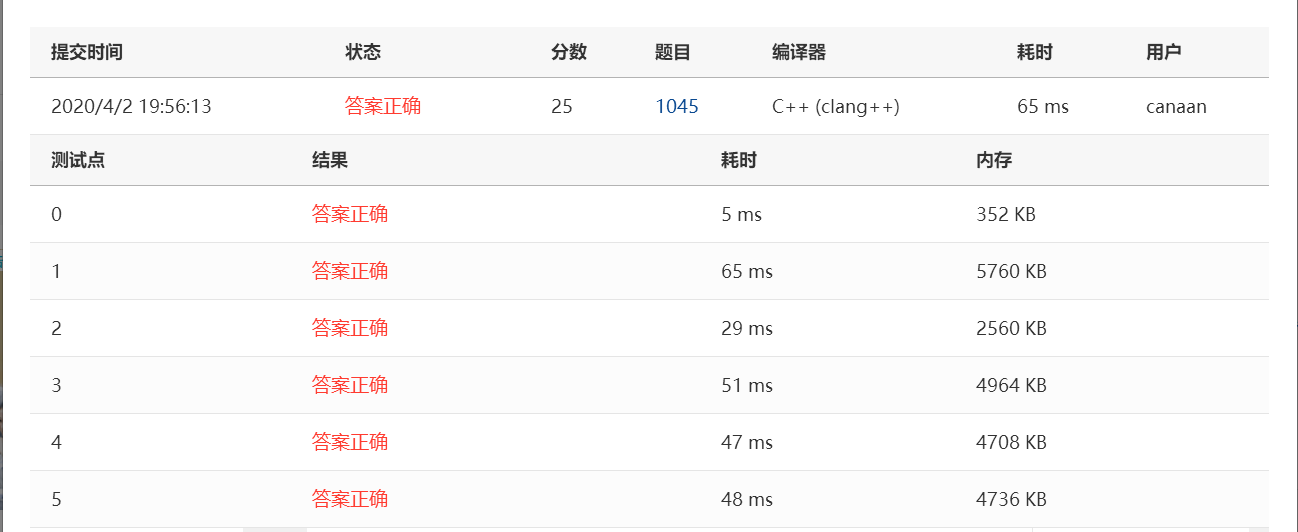
AC代码:
#include<stdio.h> #include<algorithm> using namespace std; int i,j,n; int a[100005]; int num[100005]; struct Tree{ int l,r,maxx,minn; }t[400005]; void built(int i,int l,int r){ t[i].l=l; t[i].r=r; if(l==r){ t[i].maxx=a[l]; t[i].minn=a[l]; return; } int mid=(l+r)/2; built(i*2,l,mid); built(i*2+1,mid+1,r); t[i].maxx=max(t[i*2].maxx,t[i*2+1].maxx); t[i].minn=min(t[i*2].minn,t[i*2+1].minn); } int mi(int i,int l,int r){ if(l==t[i].l && r==t[i].r){ return t[i].minn; } int mid=(t[i].l+t[i].r)/2; if(r<=mid){ return mi(i*2,l,r); } else if(l>mid){ return mi(i*2+1,l,r); } else{ return min(mi(i*2,l,mid),mi(i*2+1,mid+1,r)); } } int ma(int i,int l,int r){ if(l==t[i].l && r==t[i].r){ return t[i].maxx; } int mid=(t[i].l+t[i].r)/2; if(r<=mid){ return ma(i*2,l,r); } else if(l>mid){ return ma(i*2+1,l,r); } else{ return max(ma(i*2,l,mid),ma(i*2+1,mid+1,r)); } } int searchmax(int i,int l,int r){ if(r==0){ return 1; } else{ return ma(1,l,r)<=a[i]; } } int searchmin(int i,int l,int r){ if(l>r){ return 1; } else{ return mi(1,l,r)>=a[i]; } } int main() { int ans=0; scanf("%d",&n); for(i=1;i<=n;i++){ scanf("%d",&a[i]); } built(1,1,n); for(j=1;j<=n;j++){ if(searchmax(j,1,j-1) && searchmin(j,j+1,n)){ num[ans]=a[j]; ans++; } } printf("%d\n",ans); if(ans==0){ printf("\n"); return 0; } sort(num,num+ans); for(i=0;i<ans-1;i++){ printf("%d ",num[i]); } printf("%d",num[ans-1]); }
#include<stdio.h>
#include<algorithm>
using namespace std;
int i,j,n;
int a[100005];
int num[100005];
struct Tree{
int l,r,maxx,minn;
}t[400005];
void built(int i,int l,int r){
t[i].l=l;
t[i].r=r;
if(l==r){
t[i].maxx=a[l];
t[i].minn=a[l];
return;
}
int mid=(l+r)/2;
built(i*2,l,mid);
built(i*2+1,mid+1,r);
t[i].maxx=max(t[i*2].maxx,t[i*2+1].maxx);
t[i].minn=min(t[i*2].minn,t[i*2+1].minn);
}
int mi(int i,int l,int r){
if(l==t[i].l && r==t[i].r){
return t[i].minn;
}
int mid=(t[i].l+t[i].r)/2;
if(r<=mid){
return mi(i*2,l,r);
}
else if(l>mid){
return mi(i*2+1,l,r);
}
else{
return min(mi(i*2,l,mid),mi(i*2+1,mid+1,r));
}
}
int ma(int i,int l,int r){
if(l==t[i].l && r==t[i].r){
return t[i].maxx;
}
int mid=(t[i].l+t[i].r)/2;
if(r<=mid){
return ma(i*2,l,r);
}
else if(l>mid){
return ma(i*2+1,l,r);
}
else{
return max(ma(i*2,l,mid),ma(i*2+1,mid+1,r));
}
}
int searchmax(int i,int l,int r){
if(r==0){
return 1;
}
else{
return ma(1,l,r)<=a[i];
}
}
int searchmin(int i,int l,int r){
if(l>r){
return 1;
}
else{
return mi(1,l,r)>=a[i];
}
}
int main()
{
int ans=0;
scanf("%d",&n);
for(i=1;i<=n;i++){
scanf("%d",&a[i]);
}
built(1,1,n);
for(j=1;j<=n;j++){
if(searchmax(j,1,j-1) && searchmin(j,j+1,n)){
num[ans]=a[j];
ans++;
}
}
printf("%d\n",ans);
if(ans==0){
return 0;
}
sort(num,num+ans);
for(i=0;i<ans-1;i++){
printf("%d ",num[i]);
}
printf("%d",num[ans-1]);
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号