动手深度学习
编译器:C:\Users\20258\AppData\Local\conda\conda\envs\pytorch_env\python.exe
Pre
torch.Tensor
Tensor意为“张量”,torch中其是一个封装完备的数据结构,类似多维数组,内置相当多的功能。
创建 Tensor
torch.empty(*size, *, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False, pin_memory=False, memory_format=torch.contiguous_format)
#不初始化
torch.rand (*size, *, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False, pin_memory=False, memory_format=torch.contiguous_format)
#随机
torch.randn(*size, *, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False, pin_memory=False, memory_format=torch.contiguous_format)
#标准正态分布随机
torch.zeros(*size, *, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False, pin_memory=False, memory_format=torch.contiguous_format)
#全0
torch.ones (*size, *, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False, pin_memory=False, memory_format=torch.contiguous_format)
#全1
生成一个 size 大小的 tensor,其中 size 是一个元组(向量),out 指定结果存储位置(若无则创建新临时参量),dtype 为数据类型(默认为 torch.float32),layout 和 device 分别是内存布局、存储设备,pin_memory 表示是否固定内存,memory_format 指定内存格式。而 requires_grad 指定张量是否需要计算梯度(用于自动微分)。
当然也可以支持构造创建,使用嵌套列表 [ [,], [,] ] 即可。
torch.tensor(data, *, dtype=None, device=None, requires_grad=False, pin_memory=False)
对于复制创建,分需求为两种:
- 只用属性不用
data,可以考虑成员函数new_empty/full/zeros/ones(即new_*),需要修改某一属性直接重写参数即可(其中full表示全为指定值,需要额外给定参数fill_value值) - 只用属性不用
data,且不改变大小的,可以考虑标准函数*_like,需要修改某一属性直接重写参数即可。此时支持随机分布函数rand/randn/randint(randint表示随机指定范围 \([low, high)\) 的整数) - 需要用到
data,考虑视图的克隆x[l1:r1, l2:r2, l3:r3].clone(),或复制成员函数y.copy_(x[l1:r1, l2:r2, l3:r3])
其他常用创建函数以及功能
| 标准函数 | 功能 |
|---|---|
| Tensor(sizes) | 基础构造函数 |
| tensor(data,) | 类似np.array的构造函数 |
| ones(sizes) | 全1Tensor |
| zeros(sizes) | 全0Tensor |
| eye(sizes) | 对角线为1,其他为0 |
| arange(s,e,step) | 从s到e,步长为step |
| linspace(s,e,steps) | 从s到e,均匀切分成steps份 |
| rand/randn(*sizes) | 均匀/标准分布 |
| normal(mean,std)/uniform(from,to) | 正态分布/均匀分布 |
| randperm(m) | 随机排列 |
Tensor 的数值计算
| 标准函数 | 功能 |
|---|---|
| trace | 对角线元素之和(矩阵的迹) |
| diag | 对角线元素 |
| triu/tril | 矩阵的上三角/下三角,可指定偏移量 |
| mm/bmm | 矩阵乘法,batch的矩阵乘法 |
| addmm/addbmm/addmv/addr/baddbmm.. | 矩阵运算 |
| t | 转置 |
| dot/cross | 内积/外积 |
| inverse | 求逆矩阵 |
| svd | 奇异值分解 |
广播机制
当对两个形状不同的tensor按元素运算时,可能会触发广播(broadcasting)机制:先适当复制元素使这两个 tensor 形状相同后再按元素运算。例如:
x = torch.arange(1, 3).view(1, 2)
print(x)
y = torch.arange(1, 4).view(3, 1)
print(y)
print(x + y)
输出:
tensor([[1, 2]])
tensor([[1],
[2],
[3]])
tensor([[2, 3],
[3, 4],
[4, 5]])
由于x和y分别是1行2列和3行1列的矩阵,如果要计算x + y,那么x中第一行的2个元素被广播(复制)到了第二行和第三行,而y中第一列的3个元素被广播(复制)到了第二列。如此,就可以对2个3行2列的矩阵按元素相加。
tensor([[1, 2],
[1, 2],
[1, 2]])
+
tensor([[1, 1],
[2, 2],
[3, 3]])
误区
tensor 是一个智能指针,更确切的,是一个“数据访问器”。
一个 tensor 作为右值出现时,是一个完整 Python 对象引用。
人话来讲 x=y 是类指针引用赋值
自动求梯度
什么是梯度
对于函数 \(f(x_1,x_2,\dots,x_n)\),梯度是向量:
Tensor是这个包的核心类,如果将其属性.requires_grad设置为True,它将开始追踪(track)在其上的所有操作(这样就可以利用链式法则进行梯度传播了)。完成计算后,可以调用.backward()来完成所有梯度计算。此Tensor的梯度将累积到.grad属性中。注意在y.backward()时,如果y是标量,则不需要为backward()传入任何参数;否则,需要传入一个与y同形的Tensor。解释见 2.3.2 节。
如果不想要被继续追踪,可以调用
.detach()将其从追踪记录中分离出来,这样就可以防止将来的计算被追踪,这样梯度就传不过去了。此外,还可以用with torch.no_grad()将不想被追踪的操作代码块包裹起来,这种方法在评估模型的时候很常用,因为在评估模型时,我们并不需要计算可训练参数(`requires_grad=True``)的梯度。
Function是另外一个很重要的类。Tensor和Function互相结合就可以构建一个记录有整个计算过程的有向无环图(DAG)。每个Tensor都有一个.grad_fn属性,该属性即创建该Tensor的Function, 就是说该Tensor是不是通过某些运算得到的,若是,则grad_fn返回一个与这些运算相关的对象,否则是None。
计算图
计算图是记录计算过程的流程图。在PyTorch中,它自动跟踪所有运算,是自动微分的核心概念
示例
import torch
x = torch.ones(2, 2, requires_grad=True)
print(x)
print(x.grad_fn)
y=x+2
print(y)
print(y.grad_fn)
z = y * y * 3
out = z.mean() # 求平均值
print(z, out)
a = torch.randn(2, 2) # 缺失情况下默认 requires_grad = False
a = ((a * 3) / (a - 1))
print(a.requires_grad) # False
a.requires_grad_(True)
print(a.requires_grad) # True
b = (a * a).sum() # 求和
print(b.grad_fn)
输出
tensor([[1., 1.],
[1., 1.]], requires_grad=True)
None
tensor([[3., 3.],
[3., 3.]], grad_fn=<AddBackward0>)
<AddBackward0 object at 0x000002889917FFD0>
tensor([[27., 27.],
[27., 27.]], grad_fn=<MulBackward0>) tensor(27., grad_fn=<MeanBackward0>)
False
True
<SumBackward0 object at 0x000002889917FFD0>
人话来说就是追溯某个 tensor 被得到的计算路径。
梯度
在上面过程中
x = torch.ones(2, 2, requires_grad=True)
y=x+2
z = y * y * 3
y和z都是关于 x 的函数:
但是 torch 默认库只能直接对标量 z 求梯度,操作为
out.backward()
print(x.grad)
注意 PyTorch 默认只保留叶子节点的梯度,不保留中间节点的梯度,也就是说 y.grad 是 None。
输出:
tensor([[4.5000, 4.5000],
[4.5000, 4.5000]])
这是因为 \(z=\frac{1}{4} \sum_{i=1}^{4} 3(x_i+2)^2\) 对于每个 \(x_i\), \(\frac{\partial z}{\partial x_i}|_{x_i=1}=\frac{6(x_i+2)}{4}=4.5\)
另一个例子:
import torch
x = torch.ones(2, 2, requires_grad=True)
z = torch.zeros(2, 2, requires_grad=True)
y=x+2
w = y * (z+5) * 3
out = w.mean()
out.backward()
print(x.grad)
print(z.grad)
输出
tensor([[3.7500, 3.7500],
[3.7500, 3.7500]])
tensor([[2.2500, 2.2500],
[2.2500, 2.2500]])
1.计算图是共享的:从同一个中间结果创建的输出共享计算图
1.一次性使用:backward() 默认会释放整个计算图
1.提前定义没用:即使提前定义 sum,它仍然依赖 z 的计算图
1.保留计算图:使用 .backward(retain_graph=True) 或 torch.autograd.grad
1.有共同祖先的节点共享祖先到该点的子图
深度学习基础
线性回归
生成数据集
我们构造一个简单的人工训练数据集,它可以使我们能够直观比较学到的参数和真实的模型参数的区别。设训练数据集样本数为 \(n\),输入个数(特征数)为 2。给定随机生成的批量样本特征 \(X \in \mathbb{R}^{1000 \times 2}\),我们使用线性回归模型真实权重 \(w=[4, -3.2]^T\) 和偏差 \(b=4.2\),以及一个随机噪声项 \(\epsilon\) 来生成标签
其中噪声项 \(\epsilon\) 服从均值为 0、标准差为 0.01 的正态分布。噪声代表了数据集中无意义的干扰。下面,让我们生成数据集。
import matplotlib.pyplot as plt
import numpy as np
import torch
from IPython import display
from matplotlib import pyplot as plt
import numpy as np
import random
work = 1
if work:
num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
features = torch.randn(num_examples, num_inputs, dtype=torch.float32) # 1000*2 浮点 随机数
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b # 线性表达式 2*features[i][0]-3.4*features[i][1]+4.2
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=torch.float32) # 添加噪声
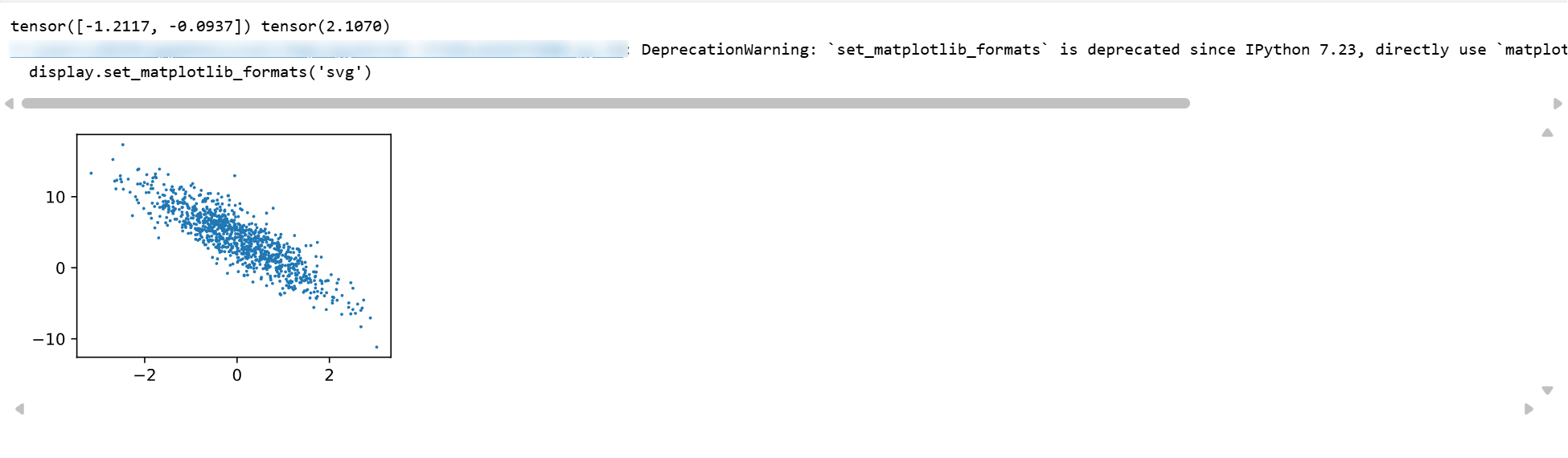
通过生成第二个特征 features[:, 1] 和标签 labels 的散点图,可以更直观地观察两者间的线性关系。
import matplotlib.pyplot as plt
import numpy as np
import torch
from IPython import display
from matplotlib import pyplot as plt
import numpy as np
import random
work = 1
if work:
num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
features = torch.randn(num_examples, num_inputs, dtype=torch.float32) # 1000*2 浮点 随机数
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b # 线性表达式 2*features[i][0]-3.4*features[i][1]+4.2
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=torch.float32) # 添加噪声
print(features[0], labels[0])
def use_svg_display():
# 用矢量图显示
display.set_matplotlib_formats('svg')
def set_figsize(figsize=(3.5, 2.5)):
use_svg_display()
# 设置图的尺寸
plt.rcParams['figure.figsize'] = figsize
# # 在../d2lzh_pytorch里面添加上面两个函数后就可以这样导入
# import sys
# sys.path.append("..")
# from d2lzh_pytorch import *
set_figsize()
plt.scatter(features[:, 1].numpy(), labels.numpy(), 1);
读取数据
在训练模型的时候,我们需要遍历数据集并不断读取小批量数据样本。这里我们定义一个函数:它每次返回 batch_size(批量大小)个随机样本的特征和标签。
# 本函数已保存在d2lzh包中方便以后使用
def data_iter(batch_size, features, labels):
num_examples = len(features)
indices = list(range(num_examples))
random.shuffle(indices) # 样本的读取顺序是随机的
for i in range(0, num_examples, batch_size):
j = torch.LongTensor(indices[i: min(i + batch_size, num_examples)]) # 最后一次可能不足一个batch
yield features.index_select(0, j), labels.index_select(0, j)
通过实例能很好看出其用法
import matplotlib.pyplot as plt
import numpy as np
import torch
from IPython import display
from matplotlib import pyplot as plt
import numpy as np
import random
import sys
sys.path.append("..")
from d2lzh_pytorch import *
work = 1
if work:
num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
features = torch.zeros(num_examples, num_inputs, dtype=torch.float32)
for i in range(num_examples):
features[i][0]=i+1 # 1-1000 的顺序放置
labels = features + 1
batch_size = 10
for X, y in data_iter(batch_size, features, labels):
print(X, y)
break
输出
tensor([[228., 0.],
[472., 0.],
[993., 0.],
[136., 0.],
[900., 0.],
[586., 0.],
[552., 0.],
[667., 0.],
[ 2., 0.],
[ 78., 0.]]) tensor([[229., 1.],
[473., 1.],
[994., 1.],
[137., 1.],
[901., 1.],
[587., 1.],
[553., 1.],
[668., 1.],
[ 3., 1.],
[ 79., 1.]])
初始化模型参数
我们将权重初始化成均值为 0、标准差为 0.01 的正态随机数,偏差则初始化成0。
w = torch.tensor(np.random.normal(0, 0.01, (num_inputs, 1)), dtype=torch.float32)
b = torch.zeros(1, dtype=torch.float32)
之后的模型训练中,需要对这些参数求梯度来迭代参数的值,因此我们要让它们的requires_grad=True。
w.requires_grad_(requires_grad=True)
b.requires_grad_(requires_grad=True)
定义模型
下面是线性回归的矢量计算表达式的实现。我们使用mm函数做矩阵乘法。
def linreg(X, w, b): # 本函数已保存在d2lzh_pytorch包中方便以后使用
return torch.mm(X, w) + b
损失函数 与 优化算法
d2lzh_pytorch 内置了损失函数和小批量随机梯度下降算法
其中 \(\hat{y}\) 是预测值,\(\theta\) 是参数(params)
\(\eta\):学习率 (lr),或者说是学习步长
\(\nabla L\):梯度
\(m\):批次大小 (batch_size)
def squared_loss(y_hat, y): # 本函数已保存在d2lzh_pytorch包中方便以后使用
# 注意这里返回的是向量, 另外, pytorch里的MSELoss并没有除以 2
return (y_hat - y.view(y_hat.size())) ** 2 / 2
def sgd(params, lr, batch_size): # 本函数已保存在d2lzh_pytorch包中方便以后使用
for param in params:
param.data -= lr * param.grad / batch_size # 注意这里更改param时用的param.data (不影响计算图)
# 更新参数:原值 - 学习率 × 梯度 / 批次大小
实例:
import matplotlib.pyplot as plt
import numpy as np
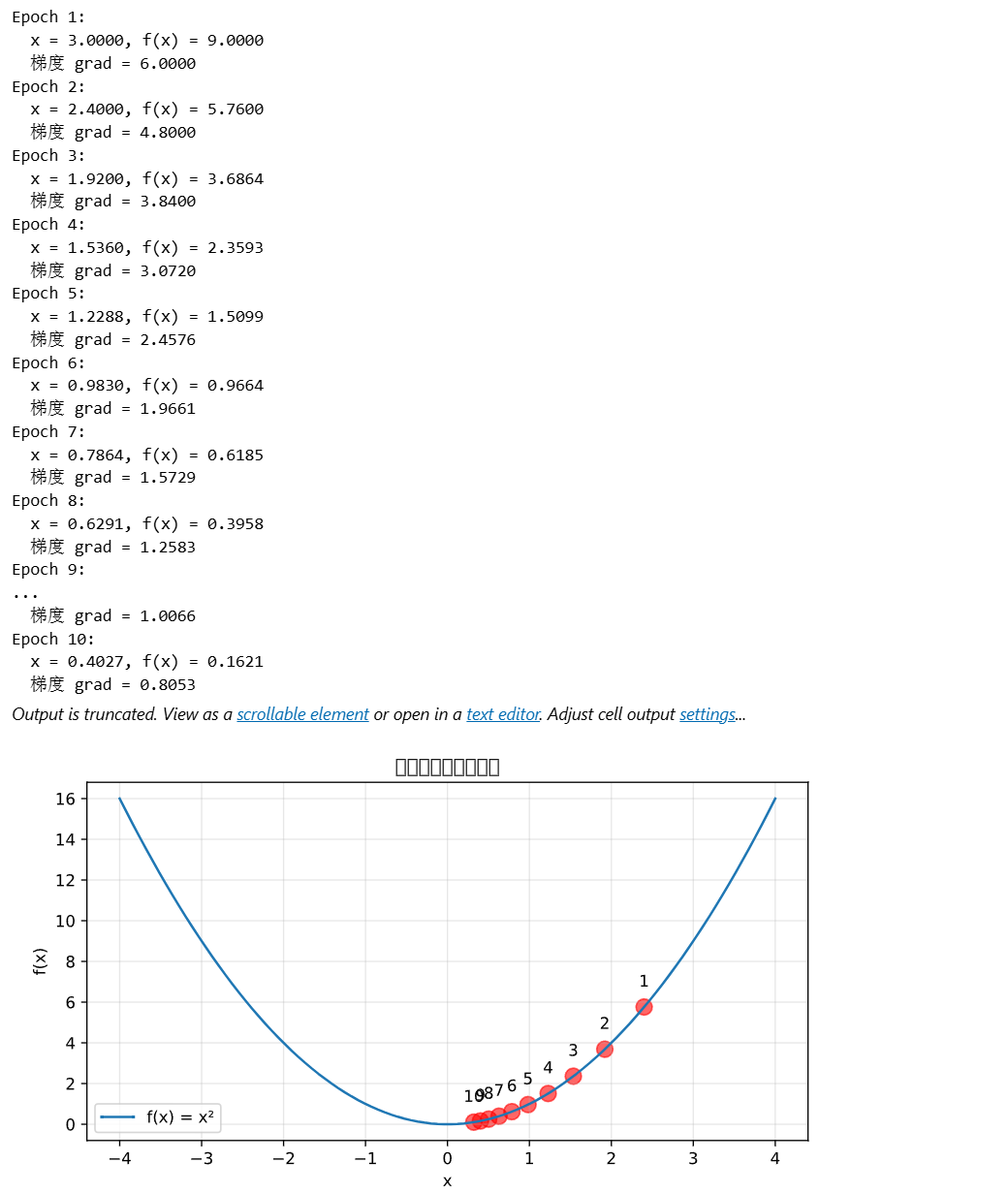
# 可视化梯度下降过程
def visualize_gradient_descent():
# 假设一个简单的二次函数:f(x) = x²
x = torch.tensor([3.0], requires_grad=True)
learning_rate = 0.1
positions = []
for epoch in range(10):
# 前向传播
y = x ** 2
# 反向传播
y.backward()
print(f"Epoch {epoch+1}:")
print(f" x = {x.item():.4f}, f(x) = {y.item():.4f}")
print(f" 梯度 grad = {x.grad.item():.4f}")
# 使用sgd更新(这里batch_size=1)
x.data -= learning_rate * x.grad / 1
positions.append(x.item())
# 清零梯度
x.grad.zero_()
# 绘制
plt.figure(figsize=(8, 4))
x_range = np.linspace(-4, 4, 100)
y_range = x_range ** 2
plt.plot(x_range, y_range, label='f(x) = x²')
plt.scatter(positions, np.array(positions)**2, c='red', s=100, alpha=0.6)
for i, (px, py) in enumerate(zip(positions, np.array(positions)**2)):
plt.text(px, py+1, f'{i+1}', ha='center')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('梯度下降过程可视化')
plt.grid(True, alpha=0.3)
plt.legend()
plt.show()
visualize_gradient_descent()
如何训练模型
在训练中,我们将多次迭代模型参数。在每次迭代中,我们根据当前读取的小批量数据样本(特征X和标签y),通过调用反向函数backward计算小批量随机梯度,并调用优化算法sgd迭代模型参数。由于我们之前设批量大小batch_size为10,每个小批量的损失l的形状为(10, 1)。回忆一下自动求梯度一节。由于变量l并不是一个标量,所以我们可以调用.sum()将其求和得到一个标量,再运行l.backward()得到该变量有关模型参数的梯度。注意在每次更新完参数后不要忘了将参数的梯度清零。
在一个迭代周期(epoch)中,我们将完整遍历一遍data_iter函数,并对训练数据集中所有样本都使用一次(假设样本数能够被批量大小整除)。这里的迭代周期个数num_epochs和学习率lr都是超参数,分别设3和0.03。在实践中,大多超参数都需要通过反复试错来不断调节。虽然迭代周期数设得越大模型可能越有效,但是训练时间可能过长。而有关学习率对模型的影响,我们会在后面“优化算法”一章中详细介绍。
lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss
for epoch in range(num_epochs): # 训练模型一共需要num_epochs个迭代周期
# 在每一个迭代周期中,会使用训练数据集中所有样本一次(假设样本数能够被批量大小整除)。X
# 和y分别是小批量样本的特征和标签
for X, y in data_iter(batch_size, features, labels):
l = loss(net(X, w, b), y).sum() # l是有关小批量X和y的损失
l.backward() # 小批量的损失对模型参数求梯度
sgd([w, b], lr, batch_size) # 使用小批量随机梯度下降迭代模型参数
# 不要忘了梯度清零
w.grad.data.zero_()
b.grad.data.zero_()
train_l = loss(net(features, w, b), labels)
print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item()))
示例:
import matplotlib.pyplot as plt
import numpy as np
import torch
import random
import sys
sys.path.append("..")
from d2lzh_pytorch import *
work = 1
if work:
num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
features = torch.randn(num_examples, num_inputs, dtype=torch.float32)
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=torch.float32)
# w和b必须是可训练的PyTorch张量
w = torch.tensor(np.random.normal(0, 0.01, (num_inputs, 1)), dtype=torch.float32, requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# labels需要reshape为列向量
labels = labels.view(-1, 1)
batch_size = 10
lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss
# ========== 设置SVG显示 ==========
use_svg_display()
# 创建图形
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
# 存储训练过程中的数据
epoch_losses = []
for epoch in range(num_epochs):
for X, y in data_iter(batch_size, features, labels):
l = loss(net(X, w, b), y).sum()
l.backward()
sgd([w, b], lr, batch_size)
w.grad.data.zero_()
b.grad.data.zero_()
# 计算整个数据集的损失
with torch.no_grad():
train_l = loss(net(features, w, b), labels)
epoch_loss = train_l.mean().item()
epoch_losses.append(epoch_loss)
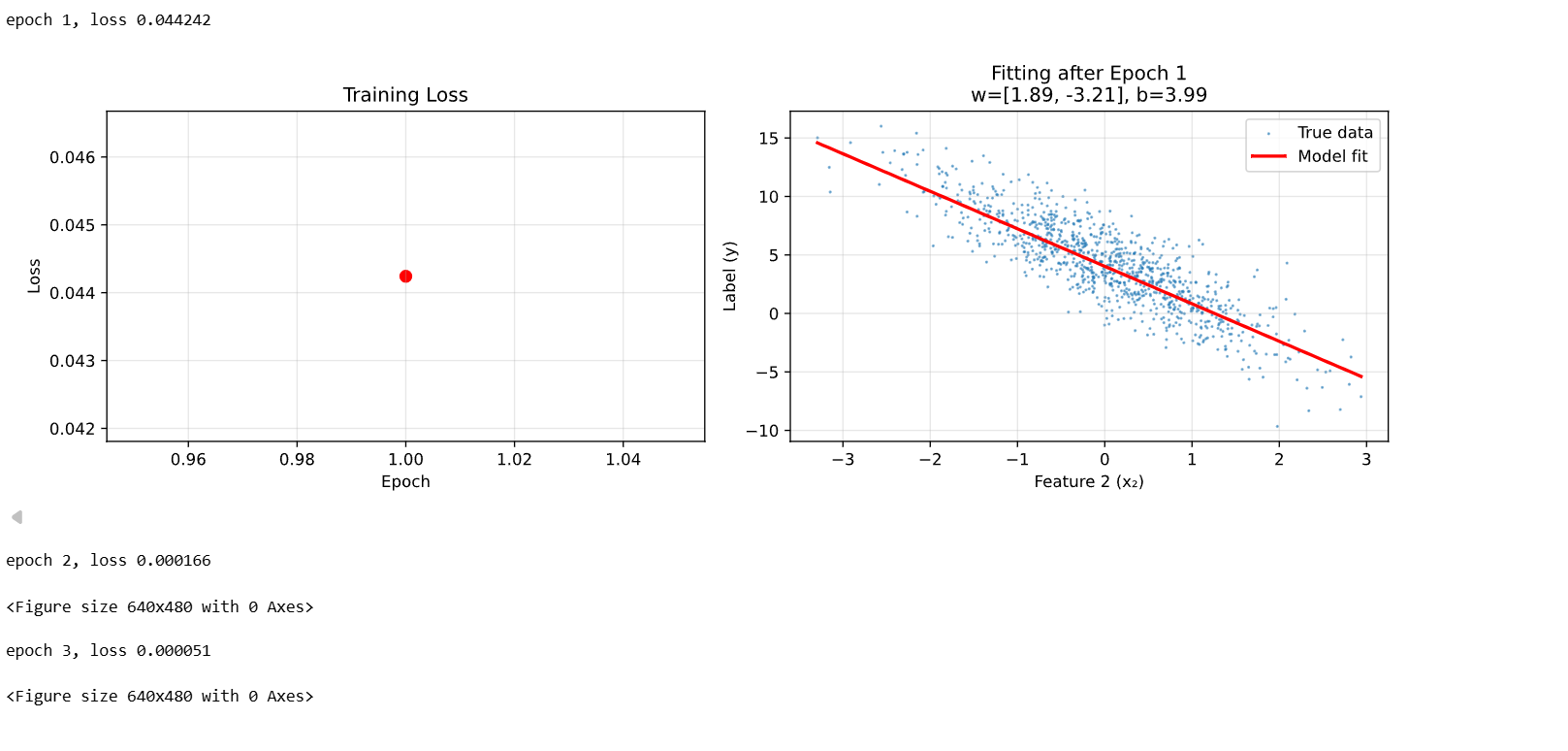
print('epoch %d, loss %f' % (epoch + 1, epoch_loss))
# ========== 实时更新可视化 ==========
# 清空之前的图形
ax1.clear()
ax2.clear()
# 图1:损失曲线
ax1.plot(range(1, epoch + 2), epoch_losses, 'b-', linewidth=2)
ax1.scatter(range(1, epoch + 2), epoch_losses, c='red', s=50)
ax1.set_xlabel('Epoch')
ax1.set_ylabel('Loss')
ax1.set_title('Training Loss')
ax1.grid(True, alpha=0.3)
# 图2:拟合效果(使用第二个特征)
ax2.scatter(features[:, 1].detach().numpy(),
labels.detach().numpy(),
s=1, alpha=0.5, label='True data')
# 绘制当前模型的拟合线
x_range = torch.linspace(features[:, 1].min(), features[:, 1].max(), 100)
# 为了简化,假设第一个特征取平均值
x1_mean = features[:, 0].mean()
y_pred = w[0].item() * x1_mean + w[1].item() * x_range + b.item()
ax2.plot(x_range.numpy(), y_pred.detach().numpy(),
'r-', linewidth=2, label='Model fit')
ax2.set_xlabel('Feature 2 (x₂)')
ax2.set_ylabel('Label (y)')
ax2.set_title(f'Fitting after Epoch {epoch+1}\nw=[{w[0].item():.2f}, {w[1].item():.2f}], b={b.item():.2f}')
ax2.legend()
ax2.grid(True, alpha=0.3)
# 更新显示
plt.tight_layout()
plt.pause(0.5) # 短暂暂停以便观察
# 保持图形显示
plt.show()


 浙公网安备 33010602011771号
浙公网安备 33010602011771号