激活函数及其梯度

Activation Functions (激活函数）

• （阈值相应机制）有多个输入，加权求和，到达阈值后输出固定的值。
  
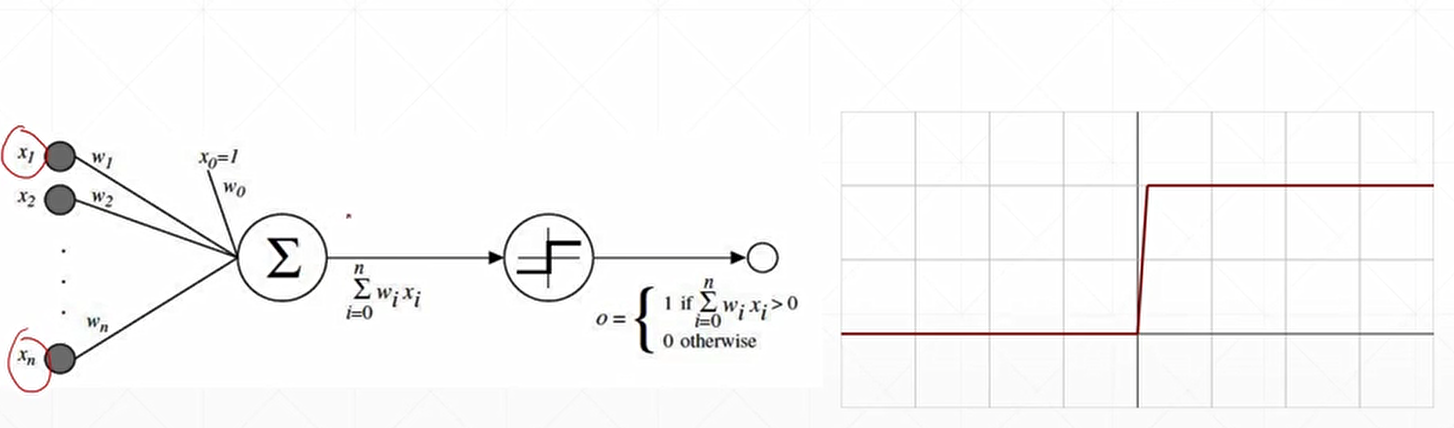
• \(Z=\sum_{i=0}^nw_ix_i\)
• \(o=f(x)= \begin{cases} 1,& \text{if }\sum_{i=0}^nw_ix_i>0 \\ 0, & \text{otherwise} \end{cases}\)

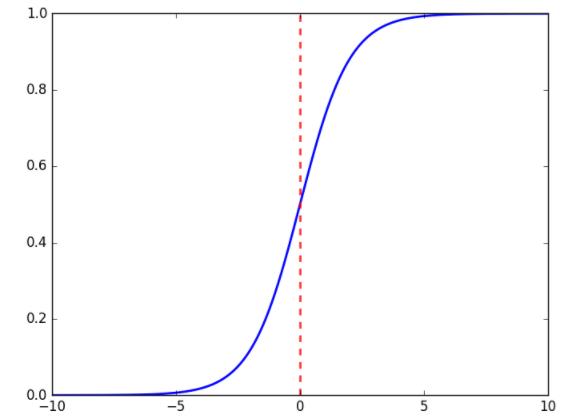
Sigmoid/Logistic

• \(f(x)=\sigma(x)=\frac{1}{1+e^{-x}}\)
  

Derivative

\(\frac{d}{dx}\sigma(x)=\frac{d}{dx}(\frac{1}{1+e^{-x}})\)
　　　　\(＝\frac{e^{-x}}{(1+e^{-x})^2}\)
　　　　\(＝\frac{1+e^{-x}-1}{(1+e^{-x})^2}\)
　　　　\(＝\frac{1+e^{-x}}{(1+e^{-x})^2}-(\frac{1}{1+e^{-x}})^2\)
　　　　\(=\sigma(x)-\sigma(x)^2\)
　　\(\sigma^{'}=\sigma(1-\sigma)\)

• 连续光滑，将输出值压缩到（0~1）

Tanh

　\(f(x)=tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}\)
　　　\(=2sigmoid(2x)-1\)

Derivative

\(\frac{d}{dx}=\frac{(e^{x}+e^{-x})(e^{x}+e^{-x})-(e^{x}-e^{-x})(e^{x}-e^{-x})}{(e^{x}+e^{-x})^2}\)
\(=1-\frac{(e^{x}-e^{-x})^2}{(e^{x}+e^{-x})^2}=1-tanh^2(x)\)

Rectified Linear Unit

\(f(x)=\begin{cases} x,& \text{if x}\geq 0 \\ 0, & \text{if x<0} \end{cases}\)