花书读书笔记
第二章 线性代数
tensor有喜感的表达方式
范数
- \(L_1\)范数 曼哈顿距离(网格型规划)
- \(L_2\)范数 欧氏距离
- \(L_\infty\)范数 切比雪夫距离
- 闵可夫斯基距离

矩阵对角化以及SVD分解
\(A(B+C)=AB+AC\) \(A(B+C)=AB+AC\)
\(A(BC)=(AB)C\)
\((AB)^T=B^TA^T\) \((AB)^T=B^TA^T\)
\(x^Ty=(x^Ty^T)^T=y^Tx\)
\(A^TA\)为对称正定矩阵
一般矩阵的SVD分解
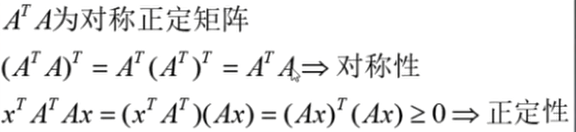


逆矩阵,伪逆矩阵,最小二乘解,最小范数解
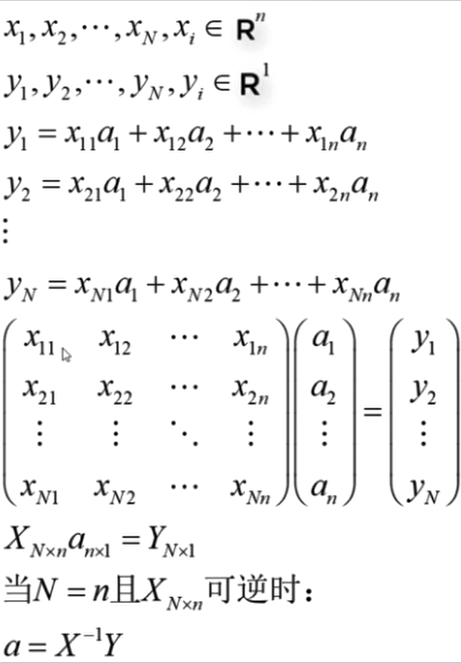
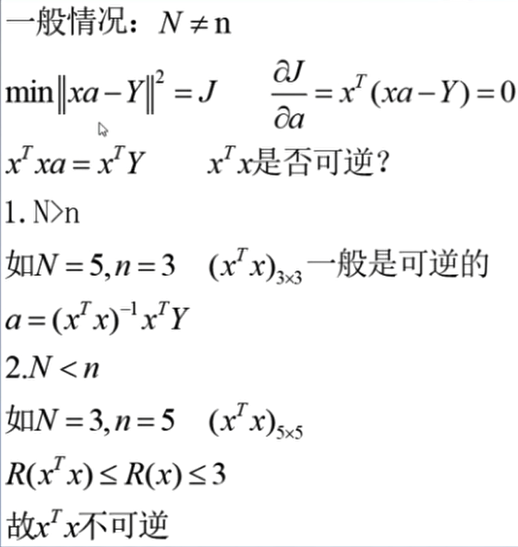 ### PCA原理及推导
### 极大似然估计,误差的高斯分布与最小二乘估计的等价性
### 最优化,无约束,有约束,拉格朗日乘子的意义,KKT条件
### PCA原理及推导
### 极大似然估计,误差的高斯分布与最小二乘估计的等价性
### 最优化,无约束,有约束,拉格朗日乘子的意义,KKT条件
PCA降维
- 二维映射到直线上,对信息进行压缩,尽可能保留高维空间的信息
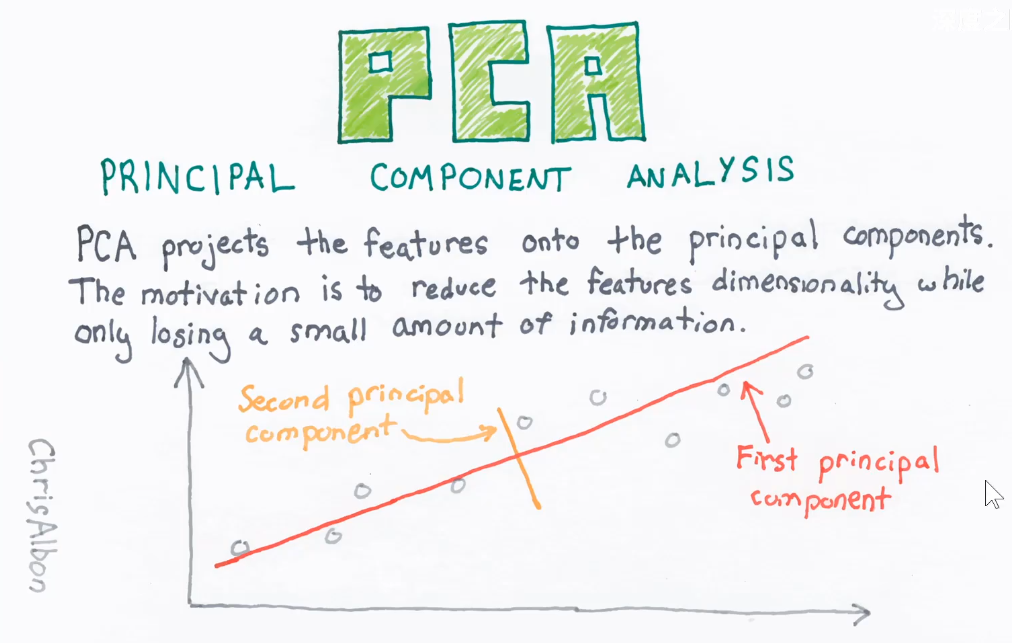
概率论与信息论
- KL散度 衡量两分布之间的差异
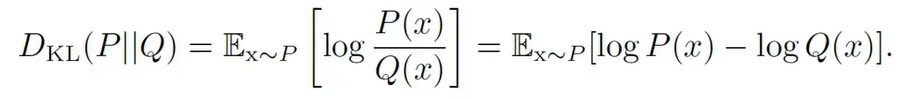
- 有向图模型
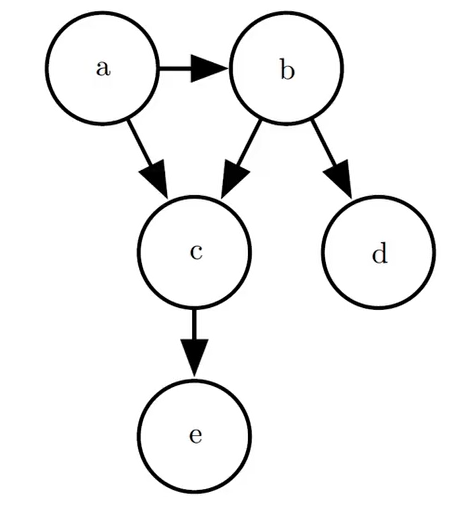
链式法则
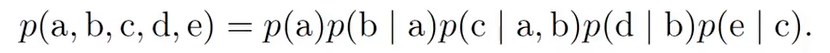


 浙公网安备 33010602011771号
浙公网安备 33010602011771号