01背包

01背包：

物品数量有限，一件物品只有两个状态：取or不取；（所以可以使用回溯法搜索出所有的情况，那么时间复杂度就是$o(2^n)$，这里的n表示物品数量。）

二维dp：

背包问题，使用二维数组，即dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。

 

有两个方向推出来dp[i][j]：

• 不放物品i：由dp[i - 1][j]推出，即背包容量为j，里面不放物品i的最大价值，此时dp[i][j]就是dp[i - 1][j]。
• 放物品i：由dp[i - 1][j - weight[i]]推出，dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值，那么dp[i - 1][j - weight[i]] + value[i] 。

递归公式： dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])。

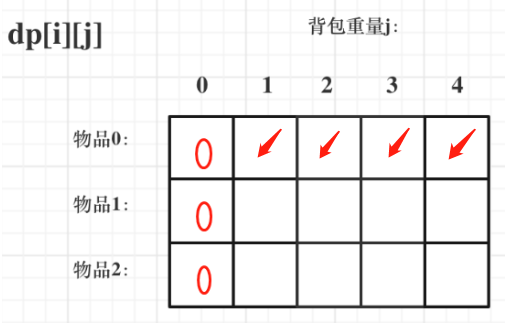
初始化，一定要和dp数组的定义吻合，否则到递推公式的时候就会越来越乱。

• 从dp[i][j]的定义出发，如果背包容量j为0的话，即dp[i][0]，无论是选取哪些物品，背包价值总和一定为0。
• 且i 是由 i-1 推导出来，那么i为0的时候就一定要初始化。dp[0][j]，即：i为0，存放编号0的物品的时候，各个容量的背包所能存放的最大价值。

　　　　j < weight[0]：dp[0][j] 应该是 0，因为背包容量比编号0的物品重量还小。

　　　　j >= weight[0]：dp[0][j] 应该是value[0]，因为背包容量放足够放编号0物品。

 

 完整代码如下：

void test_2_wei_bag_problem1() {
    vector<int> weight = {1, 3, 4};
    vector<int> value = {15, 20, 30};
    int bagweight = 4;

    // 二维数组
    vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));

    // 初始化
    for (int j = weight[0]; j <= bagweight; j++) {
        dp[0][j] = value[0];
    }

    // weight数组的大小 就是物品个数
    for(int i = 1; i < weight.size(); i++) { // 遍历物品
        for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
            if (j < weight[i]) dp[i][j] = dp[i - 1][j];
            else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

        }
    }

    cout << dp[weight.size() - 1][bagweight] << endl;
}

int main() {
    test_2_wei_bag_problem1();
}