练习cf1401A. Distance and Axis

题目如下
A. Distance and Axis
time limit per test1 second
memory limit per test256 megabytes
We have a point 𝐴 with coordinate 𝑥=𝑛 on 𝑂𝑋-axis. We'd like to find an integer point 𝐵 (also on 𝑂𝑋-axis), such that the absolute difference between the distance from 𝑂 to 𝐵 and the distance from 𝐴 to 𝐵 is equal to 𝑘.

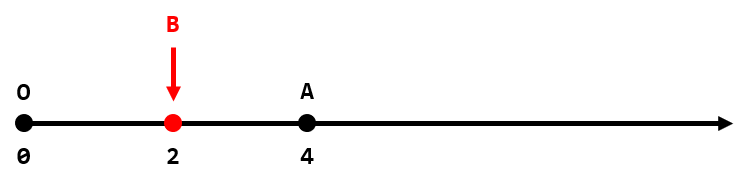
The description of the first test case.
Since sometimes it's impossible to find such point 𝐵, we can, in one step, increase or decrease the coordinate of 𝐴 by 1. What is the minimum number of steps we should do to make such point 𝐵 exist?

Input
The first line contains one integer 𝑡 (1≤𝑡≤6000) — the number of test cases.

The only line of each test case contains two integers 𝑛 and 𝑘 (0≤𝑛,𝑘≤106) — the initial position of point 𝐴 and desirable absolute difference.

Output
For each test case, print the minimum number of steps to make point 𝐵 exist.

题目大意
现有一根ox轴，点A坐标为（n，0），在轴上找到一点B，使得 | |OB| - |AB| | = k,有时根据现有的A的坐标无法直接实现，可以通过每次对A的坐标进行加或减1来改变A的坐标，问最少需要的操作次数是多少；若不需要改变A的坐标可以直接输出0.

题目分析
分两种情况，
第一种，若k > n,那么一定需要进行操作，因为无论b的坐标， | |OB| - |AB| | 一定小于n，那么只要考虑最好的情，当a至少是k时，就满足了；
第二种，若k < n,不一定需要要操作，只要当(n - k)是偶数即可，若不是，需调整一步使得(n - k)为偶数；

点击查看代码

#include <stdio.h>

int main(){
    int t;
    scanf("%d", &t);
    while(t--){
        int n, k;
        scanf("%d %d", &n, &k);
        int op;
        if(k > n){
            op = k - n;
        }else{
            op = (n - k) % 2 ;
        }
        printf("%d\n", op);
    }
    return 0;
}