# P4667 [BalticOI 2011] Switch the Lamp On 电路维修 (Day1)

P4667 [BalticOI 2011] Switch the Lamp On 电路维修 (Day1)

题目描述

Casper 正在设计电路。有一种正方形的电路元件，在它的两组相对顶点中，有一组会用导线连接起来，另一组则不会。有 $N\times M$ 个这样的元件，你想将其排列成 $N$ 行，每行 $M$ 个。 电源连接到板的左上角。灯连接到板的右下角。只有在电源和灯之间有一条电线连接的情况下，灯才会亮着。为了打开灯，任何数量的电路元件都可以转动 90°（两个方向）。

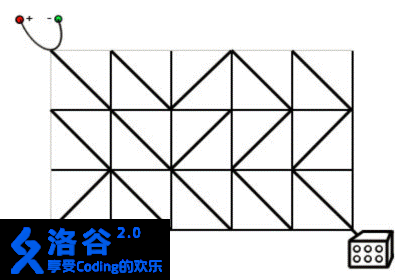
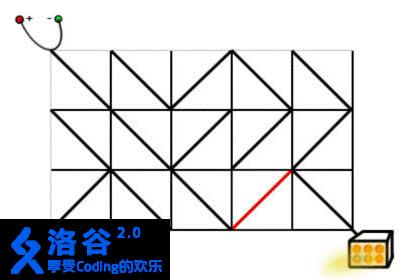
在上面的图片中，灯是关着的。如果右边的第二列的任何一个电路元件被旋转 90°，电源和灯都会连接，灯被打开。现在请你编写一个程序，求出最小需要多少旋转多少电路元件。

输入格式

输入的第一行包含两个整数 $N$ 和 $M$，表示盘子的尺寸。 在以下 $N$ 行中，每一行有 $M$ 个符号 \ 或 /，表示连接对应电路元件对角线的导线的方向。

输出格式

如果可以打开灯，那么输出只包含一个整数，表示最少转动电路元件的数量。

如果不可能打开灯，输出 NO SOLUTION。

输入输出样例 #1

输入 #1

3 5
\\/\\
\\///
/\\\\

输出 #1

1

说明/提示

对于 $40%$ 的数据，$1 \le N \le 4$，$1 \le M \le 5$。

对于所有数据，$1 \le N,M \le 500$。

这是一个bfs0-1的题目，也就是说边的权值只有0和1两种
我们将边权为 0 的路径 插入队头（front），边权为 1 的路径 插入队尾（rear），这样可以确保更小代价的路径先被扩展，维护一个严格的最短路径队列。

来看这个题目
这个题目核心的地方在于这个路线的联通问题上，怎么来处理

点击查看代码

int dx[] = {1, 1, -1, -1};
int dy[] = {1, -1, 1, -1};
int gx[] = {0, 0, -1, -1};
int gy[] = {0, -1, 0, -1};
char expected[] = {'\\', '/', '/', '\\'};

可以看到，代码里d开头代表的交点坐标的偏移，而g开头则是当前边所属的格子的坐标偏移 excepted则表示该边方向的 正确字符（\ 或 /），若当前元件与此字符一致则连通 该边方向的 正确字符（\ 或 /），若当前元件与此字符一致则连通 

点击查看代码

还有就是联通路径的处理

//如果下一条电路与预期的一致则说明联通了，否则就需要进行一次旋转操作
            int cost = (map[gx0][gy0] == expected[d]) ? 0 : 1;
            int new_step = now.step + cost;

点击查看代码

以及**bfs0-1的关键思想** ``` if (cost == 0) queue[--front] = next;//如果无需旋转优先入队，目的是寻找最短路径 else queue[rear++] = next; ```

完整代码如下

点击查看代码

#include <stdio.h>

#define MAXN 502
#define INF 1e9

typedef struct {
    int x, y,step;
}Node;

int n,m;
int map[MAXN][MAXN];
int visited[MAXN][MAXN];

int dx[] = {1, 1, -1, -1};
int dy[] = {1, -1, 1, -1};
int gx[] = {0, 0, -1, -1};
int gy[] = {0, -1, 0, -1};
char expected[] = {'\\', '/', '/', '\\'};


int BFS() {
    Node queue[MAXN * MAXN * 2];
    int front = 0, rear = 0;
    queue[rear++] = (Node) {0, 0, 0};
    visited[0][0] = 1;

    while (front < rear) {
        Node now = queue[front++];

        for (int d = 0; d < 4; d++) {
            int nx = now.x + dx[d];
            int ny = now.y + dy[d];
            int gx0 = now.x + gx[d];
            int gy0 = now.y + gy[d];
            //确保没有越界
            if (nx < 0 || nx > n || ny < 0 || ny > m)
                continue;
            if (gx0 < 0 || gx0 >= n || gy0 < 0 || gy0 >= m)
                continue;
            //如果下一条电路与预期的一致则说明联通了，否则就需要进行一次旋转操作
            int cost = (map[gx0][gy0] == expected[d]) ? 0 : 1;
            int new_step = now.step + cost;

            if (visited[nx][ny] > new_step) {
                visited[nx][ny] = new_step;
                Node next = {nx, ny, new_step};
                if (cost == 0)
                    queue[--front] = next;//如果无需旋转优先入队，目的是寻找最短路径
                else
                    queue[rear++] = next;
            }
        }
        return 1;
    }
}
int main() {
    scanf("%d %d", &n, &m);
    for (int i = 0; i < n; i++)
        scanf("%s", map[i]);

    // 初始化 visited 数组
    for (int i = 0; i <= n; i++) {
        for (int j = 0; j <= m; j++) {
            visited[i][j] = INF;
        }
    }

    int result = BFS();