# P5663 [CSP-J2019] 加工零件
P5663 [CSP-J2019] 加工零件
题目描述
凯凯的工厂正在有条不紊地生产一种神奇的零件,神奇的零件的生产过程自然也很神奇。工厂里有 $n$ 位工人,工人们从 $1 \sim n$ 编号。某些工人之间存在双向的零件传送带。保证每两名工人之间最多只存在一条传送带。
如果 $x$ 号工人想生产一个被加工到第 $L,(L \gt 1)$ 阶段的零件,则所有与 $x$ 号工人有传送带直接相连的工人,都需要生产一个被加工到第 $L - 1$ 阶段的零件(但 $x$ 号工人自己无需生产第 $L - 1$ 阶段的零件)。
如果 $x$ 号工人想生产一个被加工到第 $1$ 阶段的零件,则所有与 $x$ 号工人有传送带直接相连的工人,都需要为 $x$ 号工人提供一个原材料。
轩轩是 $1$ 号工人。现在给出 $q$ 张工单,第 $i$ 张工单表示编号为 $a_i$ 的工人想生产一个第 $L_i$ 阶段的零件。轩轩想知道对于每张工单,他是否需要给别人提供原材料。他知道聪明的你一定可以帮他计算出来!
输入格式
第一行三个正整数 $n$,$m$ 和 $q$,分别表示工人的数目、传送带的数目和工单的数目。
接下来 $m$ 行,每行两个正整数 $u$ 和 $v$,表示编号为 $u$ 和 $v$ 的工人之间存在一条零件传输带。保证 $u \neq v$。
接下来 $q$ 行,每行两个正整数 $a$ 和 $L$,表示编号为 $a$ 的工人想生产一个第 $L$ 阶段的零件。
输出格式
共 $q$ 行,每行一个字符串 Yes 或者 No。如果按照第 $i$ 张工单生产,需要编号为 1 的轩轩提供原材料,则在第 $i$ 行输出 Yes;否则在第 $i$ 行输出 No。
输入输出样例 #1
输入 #1
3 2 6
1 2
2 3
1 1
2 1
3 1
1 2
2 2
3 2
输出 #1
No
Yes
No
Yes
No
Yes
输入输出样例 #2
输入 #2
5 5 5
1 2
2 3
3 4
4 5
1 5
1 1
1 2
1 3
1 4
1 5
输出 #2
No
Yes
No
Yes
Yes
说明/提示
样例 1 说明
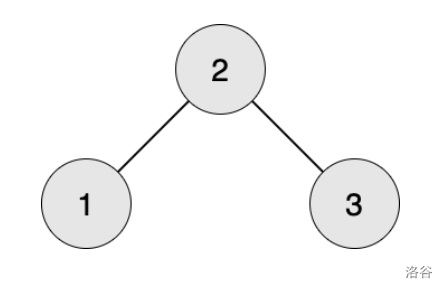
编号为 1 的工人想生产第 1 阶段的零件,需要编号为 2 的工人提供原材料。
编号为 2 的工人想生产第 1 阶段的零件,需要编号为 1 和 3 的工人提供原材料。
编号为 3 的工人想生产第 1 阶段的零件,需要编号为 2 的工人提供原材料。
编号为 1 的工人想生产第 2 阶段的零件,需要编号为 2 的工人生产第 1 阶段的零 件,需要编号为 1 和 3 的工人提供原材料。
编号为 2 的工人想生产第 2 阶段的零件,需要编号为 1 和 3 的工人生产第 1 阶段的零件,他/她们都需要编号为 2 的工人提供原材料。
编号为 3 的工人想生产第 2 阶段的零件,需要编号为 2 的工人生产第 1 阶段的零件,需要编号为 1 和 3 的工人提供原材料。
样例 2 说明
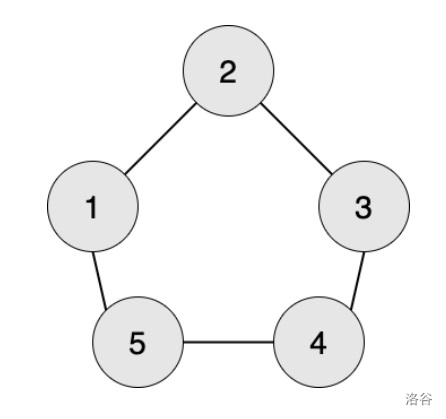
编号为 1 的工人想生产第 1 阶段的零件,需要编号为 2 和 5 的工人提供原材料。
编号为 1 的工人想生产第 2 阶段的零件,需要编号为 2 和 5 的工人生产第 1 阶段的零件,需要编号为 1,3,4 的工人提供原材料。
编号为 1 的工人想生产第 3 阶段的零件,需要编号为 2 和 5 的工人生产第 2 阶段的零件,需要编号为 1,3,4 的工人生产第 1 阶段的零件,需要编号为 2,3,4,5 的工人提供原材料。
编号为 1 的工人想生产第 4 阶段的零件,需要编号为 2 和 5 的工人生产第 3 阶段的零件,需要编号为 1,3,4 的工人生产第 2 阶段的零件,需要编号为 2,3,4,5 的工人生产第 1 阶段的零件,需要全部工人提供原材料。
编号为 1 的工人想生产第 5 阶段的零件,需要编号为 2 和 5 的工人生产第 4 阶段的零件,需要编号为 1,3,4 的工人生产第 3 阶段的零件,需要编号为 2,3,4,5 的工人生产第 2 阶段的零件,需要全部工人生产第 1 阶段的零件,需要全部工人提供原材料。
数据规模与约定
共 $20$ 个测试点。
对所有测试点保证 $1 \leq u, v, a \leq n$。
测试点 $1\sim4$,$1 \leq n, m \leq 1000$,$q = 3$,$L = 1$。
测试点 $5\sim8$,$1 \leq n, m \leq 1000$,$q = 3$,$1 \leq L \leq 10$。
测试点 $9\sim12$,$1 \leq n, m, L \leq 1000$,$1 \leq q \leq 100$。
测试点 $13\sim16$,$1 \leq n, m, L \leq 1000$,$1 \leq q \leq 10^5$。
测试点 $17\sim20$,$1 \leq n, m, q \leq 10^5$,$1 \leq L \leq 10^9$。
题目分析
这是一个邻接表求最短距离的问题
根据题目意思工人之间可能存在传送带,这是无向的,根据此我们判断是否需要1号来提供原材料,
其中还要注意员工提供原材料的层级关系
首先建立这个邻接表
点击查看代码
//建立邻接表
int head[MAXN];
int to[MAXM]; // 边指向哪个节点
int next[MAXM]; // 下一条边
int edge = 0; // 当前边的编号
int dist[MAXN]; // 表示 1 号到 i 的最短距离
// 添加一条边 u -> v
void add_edge(int u, int v) {
to[edge] = v;
next[edge] = head[u];
head[u] = edge++;
}
还有注意分析是否成立的关键
根据传送带的层阶关系,只要1号出现在供应链的任何位置就说明需要他提供原材料
点击查看代码
int need = 0;
for (int i = head[a]; i != -1; i = next[i]) {
int neighbor = to[i];
if (dist[neighbor] == l - 1) {
need = 1;
break;
}
}
if (need)
printf("Yes\n");
else
printf("No\n");
}
点击查看代码
#include <stdio.h>
#include <string.h>
#define MAXN 100001
#define MAXM 200001
//建立邻接表
int head[MAXN];
int to[MAXM]; // 边指向哪个节点
int next[MAXM]; // 下一条边
int edge = 0; // 当前边的编号
int dist[MAXN]; // 表示 1 号到 i 的最短距离
// 添加一条边 u -> v
void add_edge(int u, int v) {
to[edge] = v;
next[edge] = head[u];
head[u] = edge++;
}
void bfs(int start) {
int queue[MAXN];
int front = 0, rear = 0;
memset(dist, -1, sizeof(dist));
dist[start] = 0;
queue[rear++] = start;
while (front < rear) {
int u = queue[front++];
for (int i = head[u]; i != -1; i = next[i]) {
int v = to[i];
if (dist[v] == -1) { //判断未访问
dist[v] = dist[u] + 1;
queue[rear++] = v;
}
}
}
}
int main() {
int n, m, q;
scanf("%d %d %d", &n, &m, &q);
memset(head, -1, sizeof(head));
for (int i = 0; i < m; i++) {
int u, v;
scanf("%d %d", &u, &v);
add_edge(u, v); //因为传送带是双向的,整个图是无向图
add_edge(v, u);
}
bfs(1); // 从工人1开始BFS
while (q--) {
int a, l;
scanf("%d %d", &a, &l);
int need = 0;
for (int i = head[a]; i != -1; i = next[i]) {
int neighbor = to[i];
if (dist[neighbor] == l - 1) {
need = 1;
break;
}
}
if (need)
printf("Yes\n");
else
printf("No\n");
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号