洛谷P1126 机器人搬重物

P1126 机器人搬重物

题目描述

机器人移动学会（RMI）现在正尝试用机器人搬运物品。机器人的形状是一个直径 $1.6$ 米的球。在试验阶段，机器人被用于在一个储藏室中搬运货物。储藏室是一个 $N\times M$ 的网格，有些格子为不可移动的障碍。机器人的中心总是在格点上，当然，机器人必须在最短的时间内把物品搬运到指定的地方。机器人接受的指令有：

• 向前移动 $1$ 步（Creep）；
• 向前移动 $2$ 步（Walk）；
• 向前移动 $3$ 步（Run）；
• 向左转（Left）；
• 向右转（Right）。

每个指令所需要的时间为 $1$ 秒。请你计算一下机器人完成任务所需的最少时间。

输入格式

第一行为两个正整数 $N,M\ (1\le N,M\le50)$，下面 $N$ 行是储藏室的构造，$0$ 表示无障碍，$1$ 表示有障碍，数字之间用一个空格隔开。接着一行有 $4$ 个整数和 $1$ 个大写字母，分别为起始点和目标点左上角网格的行与列，起始时的面对方向（东 $\tt E$，南 $\tt S$，西 $\tt W$，北 $\tt N$），数与数，数与字母之间均用一个空格隔开。终点的面向方向是任意的。

输出格式

一个整数，表示机器人完成任务所需的最少时间。如果无法到达，输出 $-1$。

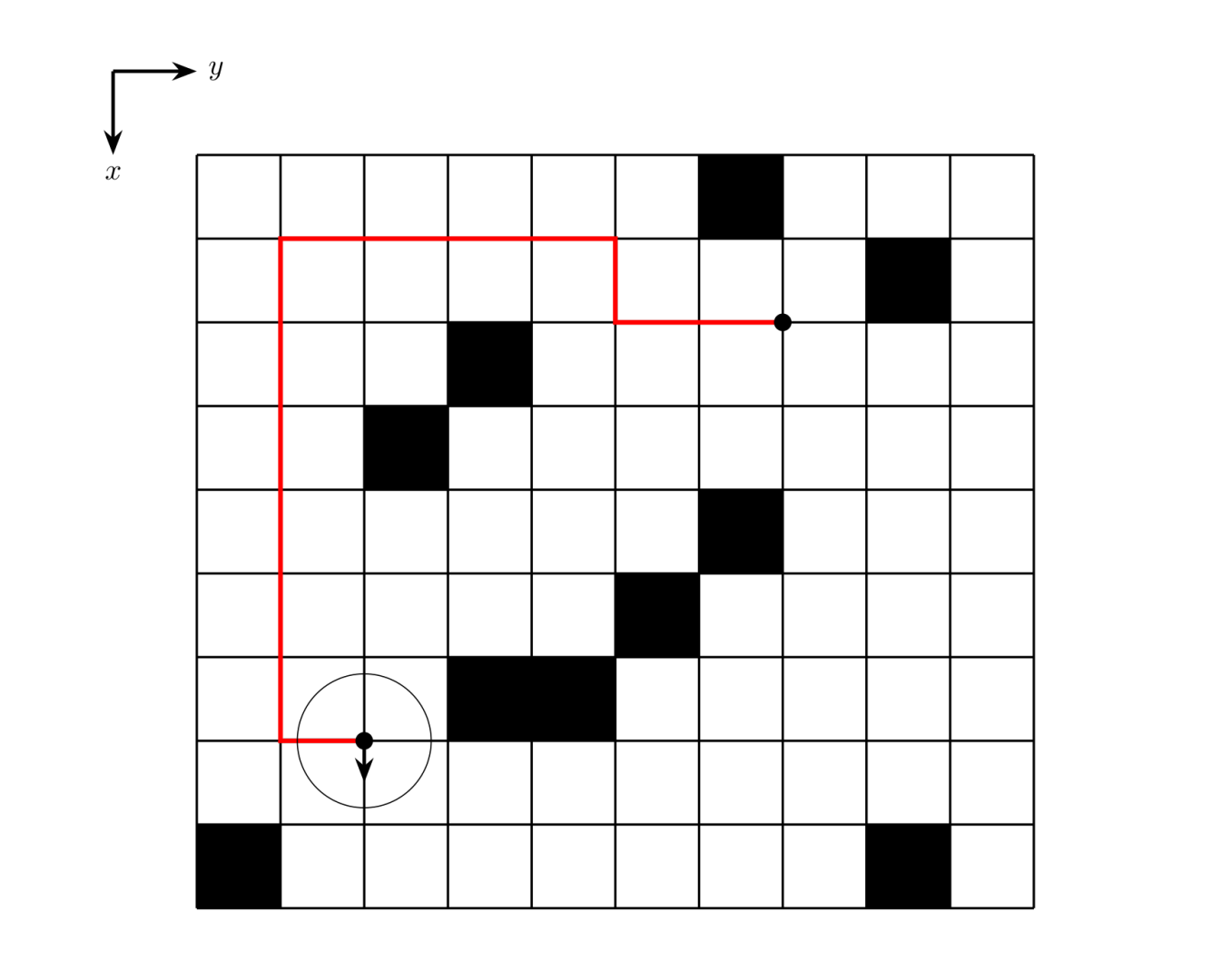
输入输出样例 #1

输入 #1

9 10
0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 0 1 0
0 0 0 1 0 0 0 0 0 0
0 0 1 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 1 0 0 0 0
0 0 0 1 1 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 1 0
7 2 2 7 S

输出 #1

12

根据题目，这也是一个最短路径问题，但是这题重点在于机器人是有方向的，所以我们需要用一个三维数组来表示，
首先定义结构体
typedef struct{ int x,y,dir,step; }Node;
同时不同于其他迷宫题，本题的机器人是一个占地四格的移动目标，已知初始坐标与目标坐标，但是这两个都是这个圆形机器人的四格中的左上角的坐标，同时也要求这四格都要能通过，于是判断合理性稍微复杂
如下
int is_valid(int x,int y){ if(x <= 0 || y <= 0 || x >= n || y >= m)//没有超出边界 return 0; if(map[x-1][y-1] || map[x-1][y] || map[x][y-1] || map[x][y]) //目标周围四个点任意一个为1就说明有障碍无法通过 return 0; return 1; }

获取初始方向调用一个函数即可
int get_dir(char ch) { switch (ch) { case 'E': return 0; case 'S': return 1; case 'W': return 2; case 'N': return 3; } return -1; }

完整代码如下

点击查看代码

#include <stdio.h>
#include <string.h>
#include <stdlib.h>

#define MAXN 51

typedef struct{
    int x,y,dir,step;
}Node;

int n,m,i,j;
int map[MAXN][MAXN];
int visited[MAXN][MAXN][4]; //因为有方向所以必须要用三维数组

int dx[4] = {0, 0, -1, 1};  // 四个方向的移动
int dy[4] = {-1, 1, 0, 0};

int is_valid(int x,int y){
    if(x <= 0 || y <= 0 || x >= n || y >= m)//没有超出边界
        return 0;
    if(map[x-1][y-1] || map[x-1][y] || map[x][y-1] || map[x][y])
        //目标周围四个点任意一个为1就说明有障碍无法通过
        return 0;
    return 1;
}

int get_dir(char ch) {
    switch (ch) {
        case 'E': return 0;
        case 'S': return 1;
        case 'W': return 2;
        case 'N': return 3;
    }
    return -1;
}

int BFS(int sx, int sy, int ex, int ey, int dir){
    Node queue[MAXN * MAXN * 4];
    int front = 0, rear = 0;

    memset(visited, 0, sizeof(visited));

    queue[rear++] = (Node){sx, sy, dir, 0};
    visited[sx][sy][dir] = 1;

    while(front < rear){
        Node now = queue[front++];
        if(now.x == ex && now.y == ey)
            return now.step; //到达终点返回步数

        int ldir = (now.dir + 3) % 4;
        if (!visited[now.x][now.y][ldir]) {
            visited[now.x][now.y][ldir] = 1;
            queue[rear++] = (Node){now.x, now.y, ldir,  now.step + 1};
        }

        // 右转
        int rdir = (now.dir + 1) % 4;
        if (!visited[now.x][now.y][rdir]) {
            visited[now.x][now.y][rdir] = 1;
            queue[rear++] = (Node){now.x, now.y, rdir,  now.step + 1};
        }
        for (int k = 1; k <= 3; k++) { //步数从1开始逐渐增大，通过是否超出边界判断步子大小
            int nx = now.x + dx[now.dir] * k; //当前坐标加上方向*步数
            int ny = now.y + dy[now.dir] * k;
            if(!visited[nx][ny][now.dir] && is_valid(nx, ny)){
                queue[rear++] = (Node){nx, ny, now.dir, now.step + 1};
                visited[nx][ny][now.dir] = 1;
            }
        }
    }
    return -1; //无法到达
}

int main() {
    scanf("%d %d", &n, &m);
    for (i = 0; i < n; i++)
        for (j = 0; j < m; j++)
            scanf("%d", &map[i][j]);

    int sx, sy, ex, ey;
    char sdir[2];
    scanf("%d %d %d %d %s", &sx, &sy, &ex, &ey, sdir);
    int dir = get_dir(sdir[0]);

    int result = BFS(sx, sy, ex, ey, dir);
    printf("%d\n", result);
    return 0;
}