洛谷P1144 最短路计数

题目如下

P1443 马的遍历

题目描述

有一个 $n \times m$ 的棋盘，在某个点 $(x, y)$ 上有一个马，要求你计算出马到达棋盘上任意一个点最少要走几步。

输入格式

输入只有一行四个整数，分别为 $n, m, x, y$。

输出格式

一个 $n \times m$ 的矩阵，代表马到达某个点最少要走几步（不能到达则输出 $-1$）。

输入输出样例 #1

输入 #1

3 3 1 1

输出 #1

0    3    2    
3    -1   1    
2    1    4

说明/提示

数据规模与约定

对于全部的测试点，保证 $1 \leq x \leq n \leq 400$，$1 \leq y \leq m \leq 400$。

题目分析
首先我们发现又是一个最短路径的问题，而且根据题目意思最短路径应该不止一条
所以这题的关键除了更新最短路径还有就在最短路径数量

额我还是想用一下邻接表，虽然但是应该肯定不是最简单，应该也不是很规范

因为要构建邻接表
先准备一下结构体

来构建一下邻接表

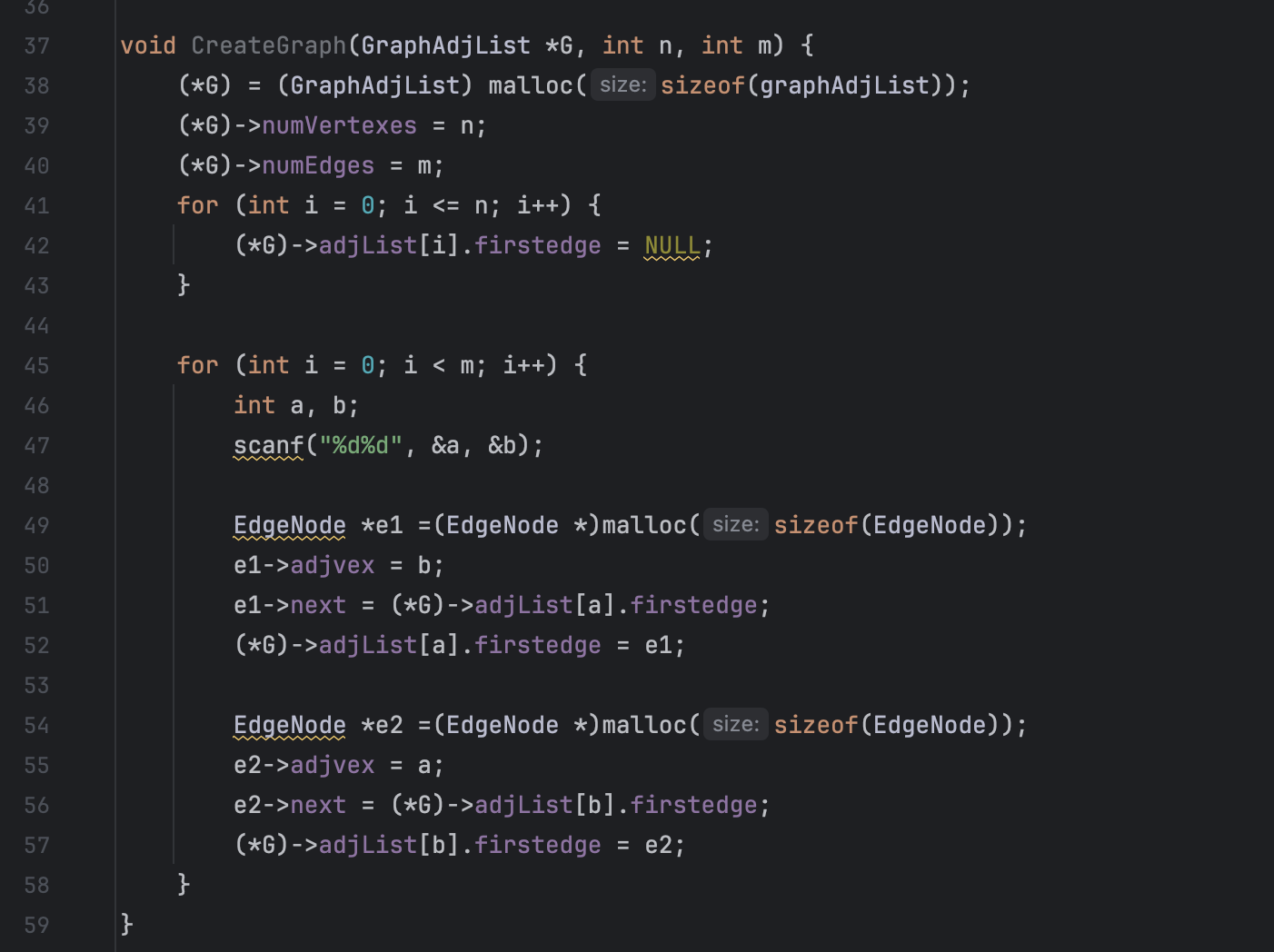
最后是BFS算法根据题目稍作改变
我们前面定义了这两个数组
int dist[MAXN]; // 到每个点的最短距离 int cnt[MAXN]; // 到每个点的最短路径条数

`void BFS(GraphAdjList *G, int start) {
memset(dist, -1, sizeof(dist));
memset(cnt, 0, sizeof(cnt));

dist[start] = 0;
cnt[start] = 1;
enqueue(start);

while (front < rear) {
    int a = dequeue();
    EdgeNode *e = (*G)->adjList[a].firstedge;
    while (e != NULL) {
        int b = e->adjvex;
        if (dist[b] == -1) {
            dist[b] = dist[a] + 1;
            cnt[b] = cnt[a];
            enqueue(b);
        } else if (dist[b] == dist[a] + 1) { //从 a 到 b 是另一条等长的最短路径，所以把 a 的路径数累加到 b 上
            cnt[b] = (cnt[b] + cnt[a]) % MOD; //对结果取模，避免结果过大
        }
        e = e->next;
    }
}

}`
在这里分了三种情况
第一种情况：dist[b] == -1
就是b 还没有被访问过，说明这是第一次找到从 a 到达 b 的路径。
第二种情况dist[b] == dist[a] + 1
b 已经被访问过，但他也是最短路径

这段代码主要是更新每个点的最短距离 dist 和从起点到该点的不同最短路径数 cnt，确保在访问图的过程中统计所有最短路径的可能。

解决完这里就可以解决了

完整代码如下
`#include <stdio.h>

include <stdlib.h>

include <string.h>

define MAXN 200006

define MOD 100003

typedef struct EdgeNode{
int adjvex;
struct EdgeNode *next;
}EdgeNode;

typedef struct VertexNode{
EdgeNode *firstedge;
}VertexNode, AdjList[MAXN];

typedef struct{
AdjList adjList; /* 所有顶点+所有边的总集合/
int numVertexes,numEdges; / 图中当前顶点数和边数 /
}graphAdjList,GraphAdjList; /* 本体 & 指针 */

int dist[MAXN]; // 到每个点的最短距离
int cnt[MAXN]; // 到每个点的最短路径条数

int queue[MAXN];
int front = 0, rear = 0; void enqueue(int x) {
queue[rear++] = x;
}

int dequeue() {
return queue[front++];
}

void CreateGraph(GraphAdjList G, int n, int m) {
(G) = (GraphAdjList) malloc(sizeof(graphAdjList));
(G)->numVertexes = n;
(G)->numEdges = m;
for (int i = 0; i <= n; i++) {
(*G)->adjList[i].firstedge = NULL;
}

for (int i = 0; i < m; i++) {
    int a, b;
    scanf("%d%d", &a, &b);

    EdgeNode *e1 =(EdgeNode *)malloc(sizeof(EdgeNode));
    e1->adjvex = b;
    e1->next = (*G)->adjList[a].firstedge;
    (*G)->adjList[a].firstedge = e1;

    EdgeNode *e2 =(EdgeNode *)malloc(sizeof(EdgeNode));
    e2->adjvex = a;
    e2->next = (*G)->adjList[b].firstedge;
    (*G)->adjList[b].firstedge = e2;
}

} void BFS(GraphAdjList *G, int start) {
memset(dist, -1, sizeof(dist));
memset(cnt, 0, sizeof(cnt));

dist[start] = 0;
cnt[start] = 1;
enqueue(start);

while (front < rear) {
    int a = dequeue();
    EdgeNode *e = (*G)->adjList[a].firstedge;
    while (e != NULL) {
        int b = e->adjvex;
        if (dist[b] == -1) {
            dist[b] = dist[a] + 1;
            cnt[b] = cnt[a];
            enqueue(b);
        } else if (dist[b] == dist[a] + 1) {
            cnt[b] = (cnt[b] + cnt[a]) % MOD;
        }
        e = e->next;
    }
}

}

int main() {
int n, m;
scanf("%d %d", &n, &m);

GraphAdjList G;
CreateGraph(&G, n, m);
BFS(&G, 1);

for (int i = 1; i <= n; ++i) {
    printf("%d\n", cnt[i]);
}

return 0;

}`
我好像知道大概要怎么写这样的题目了