洛谷P6207 （网格图，BFS 输出最短路径）

题目如下

P6207 [USACO06OCT] Cows on Skates G

题目描述

本题使用 Special Judge。

Farmer John 把农场划分为了一个 $r$ 行 $c$ 列的矩阵，并发现奶牛们无法通过其中一些区域。此刻，Bessie 位于坐标为 $(1,1)$ 的区域，并想到坐标为 $(r,c)$ 的牛棚享用晚餐。她知道，以她所在的区域为起点，每次移动至相邻的四个区域之一，总有一些路径可以到达牛棚。

这样的路径可能有无数种，请你输出任意一种，并保证所需移动次数不超过 $100000$。

输入格式

第一行两个整数 $r,c$。

接下来 $r$ 行，每行 $c$ 个字符，表示 Bessie 能否通过相应位置的区域。字符只可能是 . 或 *。

. 表示 Bessie 可以通过该区域。
* 表示 Bessie 无法通过该区域。

输出格式

若干行，每行包含两个用空格隔开的整数，表示 Bessie 依次通过的区域的坐标。

显然，输出的第一行是 1 1 ，最后一行是 r c。

相邻的两个坐标所表示的区域必须相邻。

输入输出样例 #1

输入 #1

5 8
..*...**
*.*.*.**
*...*...
*.*.*.*.
....*.*.

输出 #1

说明/提示

【数据范围】

对于 $100%$ 的数据，$1\le r\le 113$，$1\le c\le 77$。

*【样例说明】 *

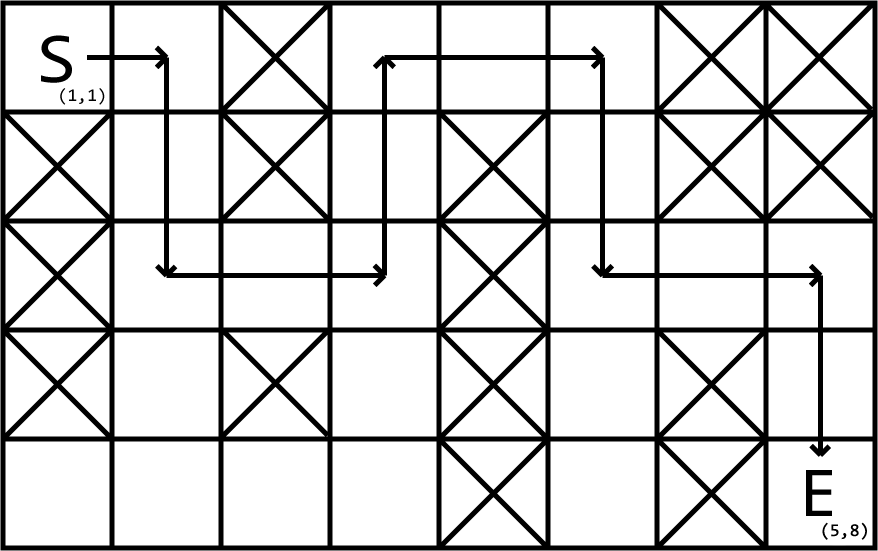
图为样例输出的示意图。答案不唯一。

题目分析
根据题目不难看出这是也是一个关于BFS求最短路径的题目，有点像前两天做的CESC1193 那个迷宫题，所以就沿用迷宫题的思路，稍微修改，这次不分开坐标直接定义一个坐标结构体
typedef struct{ int y,x; }Point;
⚠️注意，同样是先行后列，但在二维数组中，y代表行，x代表列

因为我们我们直接调用两个函数来表示出入队
void enqueue(Point p) { queue[rear++] = p; /*入队*/ } Point dequeue() { return queue[front++]; /*出队*/ }

然后我们定义BFS函数为bool类型判是否有路可走
`bool BFS(){
enqueue(start);
visited[start.y][start.x] = 1;

while(front < rear){
    Point now = dequeue();

    if(now.y == r - 1 && now.x == c - 1){
        return true;
    }

    for (int d = 0; d < 4; ++d) { /*从四个方向依次分别确认*/
        int ny = now.y + dy[d];
        int nx = now.x + dx[d];

        if (ny >= 0 && ny < r && nx >= 0 && nx < c && !visited[ny][nx] && map[ny][nx] == '.') {
            visited[ny][nx] = 1;
            parent[ny][nx] = now;
            enqueue((Point) {ny, nx}); /*新点入队*/
        }
    }
}
return false;

最后仍然是根据parent作为上一个节点来回溯复原整条路径
void printpath(){ Point path[MAXN * MAXN]; int len = 0; Point cur = end; while (!(cur.y == 0 && cur.x == 0)) { /*起点是 (0,0)*/ path[len++] = cur; cur = parent[cur.y][cur.x]; } path[len++] = (Point){0, 0}; /*加上起点*/
注意不要忘记加上起点，从起点开始也要求输出

完整代码如下`#include <stdio.h>

include <stdlib.h>

include <string.h>

define MAXN 1000

typedef struct{
int y,x;
}Point;

int r, c;
Point start, end;
char map[MAXN][MAXN];
int visited[MAXN][MAXN];
Point parent[MAXN][MAXN]; /记录上一节点便于回溯/

int dx[4] = {0, 0, -1, 1}; /* 上下左右移动*/
int dy[4] = {-1, 1, 0, 0};

Point queue[MAXN * MAXN];
int front = 0, rear = 0;

void enqueue(Point p) {
queue[rear++] = p; /入队/
}
Point dequeue() {
return queue[front++]; /出队/
}
bool BFS(){
enqueue(start);
visited[start.y][start.x] = 1;

while(front < rear){
    Point now = dequeue();

    if(now.y == r - 1 && now.x == c - 1){
        return true;
    }

    for (int d = 0; d < 4; ++d) { /*从四个方向依次分别确认*/
        int ny = now.y + dy[d];
        int nx = now.x + dx[d];

        if (ny >= 0 && ny < r && nx >= 0 && nx < c && !visited[ny][nx] && map[ny][nx] == '.') {
            visited[ny][nx] = 1;
            parent[ny][nx] = now;
            enqueue((Point) {ny, nx}); /*新点入队*/
        }
    }
}
return false;

}

void printpath(){
Point path[MAXN * MAXN];
int len = 0;
Point cur = end;
while (!(cur.y == 0 && cur.x == 0)) { /起点是 (0,0)/
path[len++] = cur;
cur = parent[cur.y][cur.x];
}
path[len++] = (Point){0, 0}; /加上起点/
/反转输出/
for (int i = len - 1; i >= 0; i--) {
printf("%d %d\n", path[i].y + 1, path[i].x + 1);
}
}

int main() {
scanf("%d %d", &r, &c);
for (int i = 0; i < r; i++) {
scanf("%s", map[i]);
}
start = {0, 0};
end = {r - 1, c - 1};

BFS();
printpath();
return 0;

记录一下，把我不懂的都写出来了，没有敷衍偷懒啊哈哈，感觉有点手感了呵呵，跟迷宫题差不多稍微改变了写法

posted @ 2025-04-29 00:10 sirro1uta 阅读(82) 评论(0) 收藏举报

刷新页面返回顶部

sirr01uta