CSES 1193 题解 bfs专练（网格图，BFS 输出最短路径）

题目如下

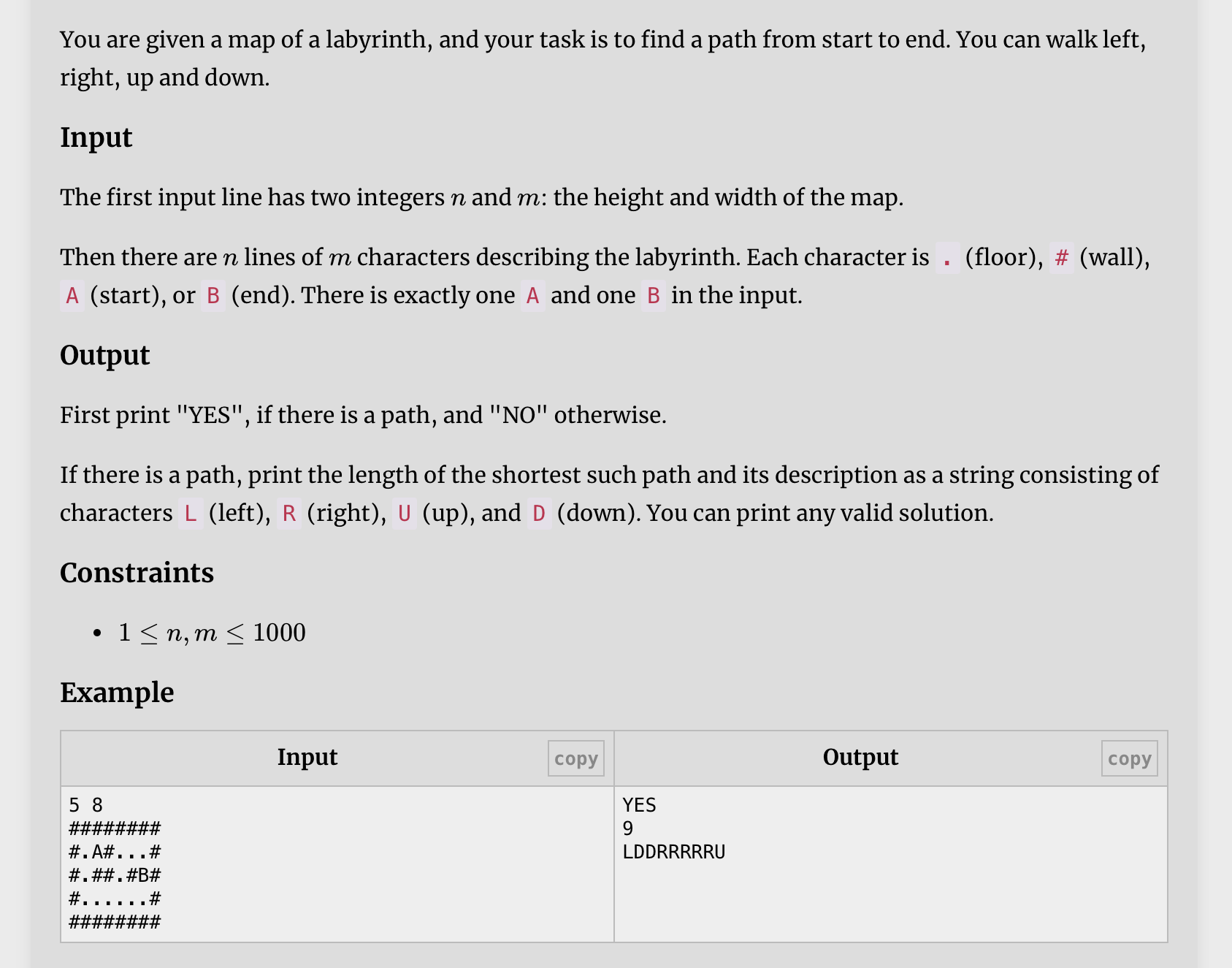
题目大意
给我们规格为n*m的迷宫，其中“#”代表墙壁，形如“.....”都代表可走路线，让我们找出从A到B的最短路径

题目分析
这是一个关于网格图，BFS输出最小路径的问题

首先我们要确定A，B的坐标
for (int j = 0; j < m; ++j) { if (laby[i][j] == 'A') { //确定A和B的横纵坐标 Ay = i; Ax = j; } else if (laby[i][j] == 'B') { By = i; Bx = j; } }
分别确定横纵坐标

根据题目规定的上下左右四个方向的移动来规定一下每次移动的坐标变化
int dx[4] = {0, 0, -1, 1}; // 上下左右移动 int dy[4] = {-1, 1, 0, 0}; char dirChar[4] = {'U', 'D', 'L', 'R'}; // 移动对应的方向字符

为了便于判断，除了visited数组，我们还需要确定上一步的坐标，以及移动的方向
`har laby[MAXN][MAXN];
int visited[MAXN][MAXN]; // 是否访问过
int fromY[MAXN][MAXN]; // 上一步坐标
int fromX[MAXN][MAXN];
char fromDir[MAXN][MAXN]; // 从哪个方向来

关键的BFS算法求最小路径
`bool BFS() {
Node queue[MAXN * MAXN];
int front = 0, rear = 0;

memset(visited, 0, sizeof(visited));

queue[rear++] = {Ay, Ax, 0};
visited[Ay][Ax] = 1;

while (front < rear) {
    Node now = queue[front++];

    if (now.y == By && now.x == Bx) {
        return true;
    }
    //如果当前位置与B坐标重合说明到达终点 立即退出
    for (int d = 0; d < 4; ++d) { //从四个方向依次分别确认
        int ny = now.y + dy[d];
        int nx = now.x + dx[d];

        if (ny >= 0 && ny < n && nx >= 0 && nx < m && !visited[ny][nx] && laby[ny][nx] != '#') {
            //防止超出迷宫并确认不是墙 并 确认未访问
            visited[ny][nx] = 1;
            queue[rear++] = {ny, nx, now.step + 1}; //令当前位置的相邻点入队
            fromY[ny][nx] = now.y;
            fromX[ny][nx] = now.x;
            fromDir[ny][nx] = dirChar[d];
        }
    }
}
return false;

}`
用bool来判断并返回是否有最短路径

如果有
void printPath() { //记录并输出路径 char path[MAXN * MAXN]; int len = 0; int y = By, x = Bx; while (!(y == Ay && x == Ax)) { path[len++] = fromDir[y][x]; //从后往前记录 int py = fromY[y][x]; int px = fromX[y][x]; y = py; x = px; } printf("%d\n", len); // 反转路径 for (int i = 0; i < len / 2; ++i) { swap(path[i], path[len - 1 - i]); } printf("%s\n", path); }
注意这里的路径从后往前记录所以输出是要进行反转

⚠️最后要注意的是我们一开始
定义结构体时
struct Node { int y, x, step; };
要按照laby[行][列]
==> laby[y][x]先列再行不要记错

完整代码如下
`#include

include <stdio.h>

include <string.h>

include

using namespace std;

define MAXN 1001

int n, m;
char laby[MAXN][MAXN];
int visited[MAXN][MAXN]; // 是否访问过
int fromY[MAXN][MAXN]; // 上一步坐标
int fromX[MAXN][MAXN];
char fromDir[MAXN][MAXN]; // 从哪个方向来

int dx[4] = {0, 0, -1, 1}; // 上下左右移动
int dy[4] = {-1, 1, 0, 0};
char dirChar[4] = {'U', 'D', 'L', 'R'}; // 移动对应的方向字符

int Ay, Ax, By, Bx; // 起点A 和终点B 的坐标

struct Node {
int y, x, step;
};

bool BFS() {
Node queue[MAXN * MAXN];
int front = 0, rear = 0;

memset(visited, 0, sizeof(visited));

queue[rear++] = {Ay, Ax, 0};
visited[Ay][Ax] = 1;

while (front < rear) {
    Node now = queue[front++];

    if (now.y == By && now.x == Bx) {
        return true;
    }
    //如果当前位置与B坐标重合说明到达终点 立即退出
    for (int d = 0; d < 4; ++d) { //从四个方向依次分别确认
        int ny = now.y + dy[d];
        int nx = now.x + dx[d];

        if (ny >= 0 && ny < n && nx >= 0 && nx < m && !visited[ny][nx] && laby[ny][nx] != '#') {
            //防止超出迷宫并确认不是墙 并 确认未访问
            visited[ny][nx] = 1;
            queue[rear++] = {ny, nx, now.step + 1}; //令当前位置的相邻点入队
            fromY[ny][nx] = now.y;
            fromX[ny][nx] = now.x;
            fromDir[ny][nx] = dirChar[d];
        }
    }
}
return false;

}

void printPath() { //记录并输出路径
char path[MAXN * MAXN];
int len = 0;
int y = By, x = Bx;
while (!(y == Ay && x == Ax)) {
path[len++] = fromDir[y][x];
int py = fromY[y][x];
int px = fromX[y][x];
y = py;
x = px;
}
printf("%d\n", len);
// 反转路径
for (int i = 0; i < len / 2; ++i) {
swap(path[i], path[len - 1 - i]);
}
printf("%s\n", path);
}

int main() {
scanf("%d %d", &n, &m);
for (int i = 0; i < n; ++i) {
scanf("%s", laby[i]); //每次输入一行
for (int j = 0; j < m; ++j) {
if (laby[i][j] == 'A') { //确定A和B的横纵坐标
Ay = i;
Ax = j;
} else if (laby[i][j] == 'B') {
By = i;
Bx = j;
}
}
}
if (BFS()) {
printf("YES\n");
printPath();
} else {
printf("NO\n");
}
return 0;
}
`

路漫漫其修远兮，苦瓜啊，加油啊