codeforces1352B. Same Parity Summands

题目在这

题目大意
就是分析能否将n分解为k个奇偶性相同的数，可以就输出yes，并输出任意一种可构成的结果，反之只要输出no就好了
那么我们来分析一下，底层逻辑是什么呢，我们都知道，
• 奇数 + 奇数 = 偶数
• 偶数 + 奇数 = 奇数
那么结合一下这张草稿分析一下

最后我们得出能够分解的情况就这么几种
先考虑n的奇偶性，
• 当n为偶数时，k为奇数时，可以分解为k个偶数
• 当n为偶数时，k也为偶数时，既可以由k个偶数组成也可由k个奇数组成，这里为了方便就不考虑奇数了
• 当n为奇数时，那么k只能是奇数，也只有k个奇数才能构成一个奇数

我们先考虑情况少的奇数的构成
用n % 2 == k % 2表示奇数个奇数构成一个奇数的情况
这里我们用最小的奇数来凑前k-1个，直到最后一个是1无法构成时，
注意，这里也包含了n=k的情况！

然后我们再考虑偶数的构成
这里我们用n >= 2*k条件加以区分，原因是考虑到我们用偶数来凑，最小的偶数是2，我们就不得不考虑到n是否够大能够容纳至少k个2，否则也是无法达到分解条件。
在满足条件后，同理我们用最小的偶数来凑前k-1个，直到最后一个是2无法构成时，根据偶数+偶数=偶数，可以省去对最后一个数奇偶的判断，因为一定是偶数，那么我们就放心的用n减去k-1个2剩下的来凑了

完整代码如下

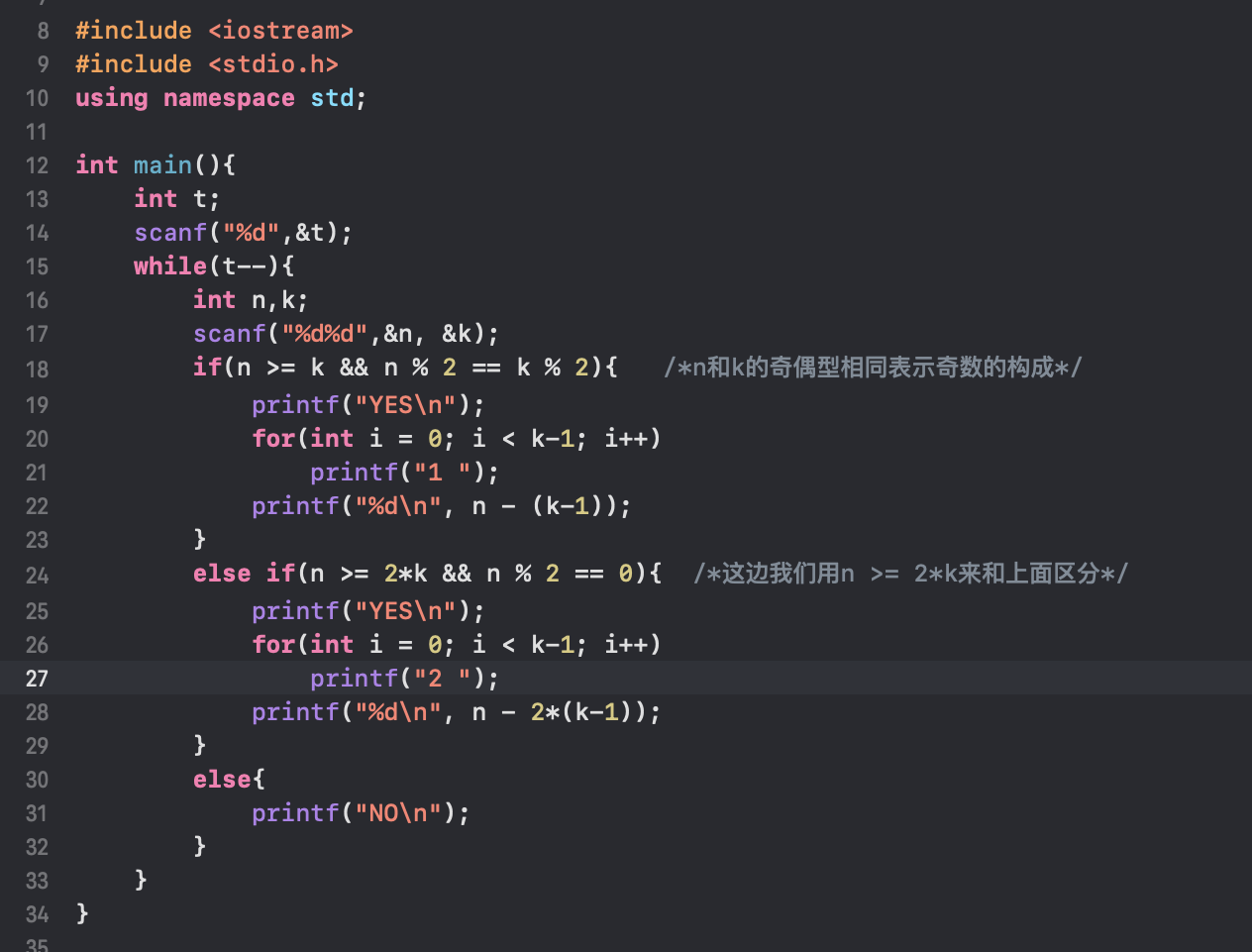
记录一下，并不是那么的水了，day几了忘了，可以的，拜拜