理论上，所有的波形数据，都可以通过不同频率和相位的正弦波或者余弦波叠加而成。所以，可以对时效数据进行FFT，找出其周期特点。

 

参考：https://www.kaggle.com/muonneutrino/wikipedia-traffic-data-exploration

 

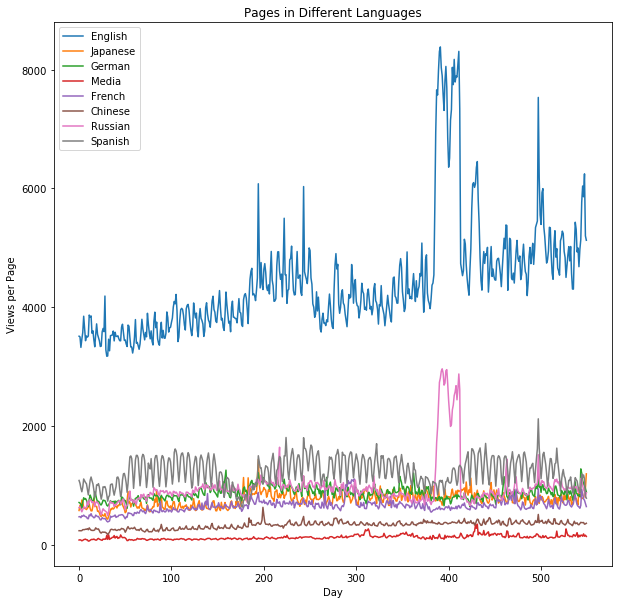
 如图所示，为各个不同语音国家访问给定的wiki页面的平均流量，可以看出，欧美国家访问量较多，且呈现出一定的周期规律（每第7天有明显的访问量增加）。

from scipy.fftpack import fft
def plot_with_fft(key):

    fig = plt.figure(1,figsize=[15,5])
    plt.ylabel('Views per Page')
    plt.xlabel('Day')
    plt.title(labels[key])
    plt.plot(days,sums[key],label = labels[key] )
    
    fig = plt.figure(2,figsize=[15,5])
    fft_complex = fft(sums[key])
    fft_mag = [np.sqrt(np.real(x)*np.real(x)+np.imag(x)*np.imag(x)) for x in fft_complex]
    fft_xvals = [day / days[-1] for day in days]
    npts = len(fft_xvals) // 2 + 1
    fft_mag = fft_mag[:npts]
    fft_xvals = fft_xvals[:npts]
        
    plt.ylabel('FFT Magnitude')
    plt.xlabel(r"Frequency [days]$^{-1}$")
    plt.title('Fourier Transform')
    plt.plot(fft_xvals[1:],fft_mag[1:],label = labels[key] )
    # Draw lines at 1, 1/2, and 1/3 week periods
    plt.axvline(x=1./7,color='red',alpha=0.3)
    plt.axvline(x=2./7,color='red',alpha=0.3)
    plt.axvline(x=3./7,color='red',alpha=0.3)

    plt.show()

for key in sums:
    plot_with_fft(key)
View Code

 

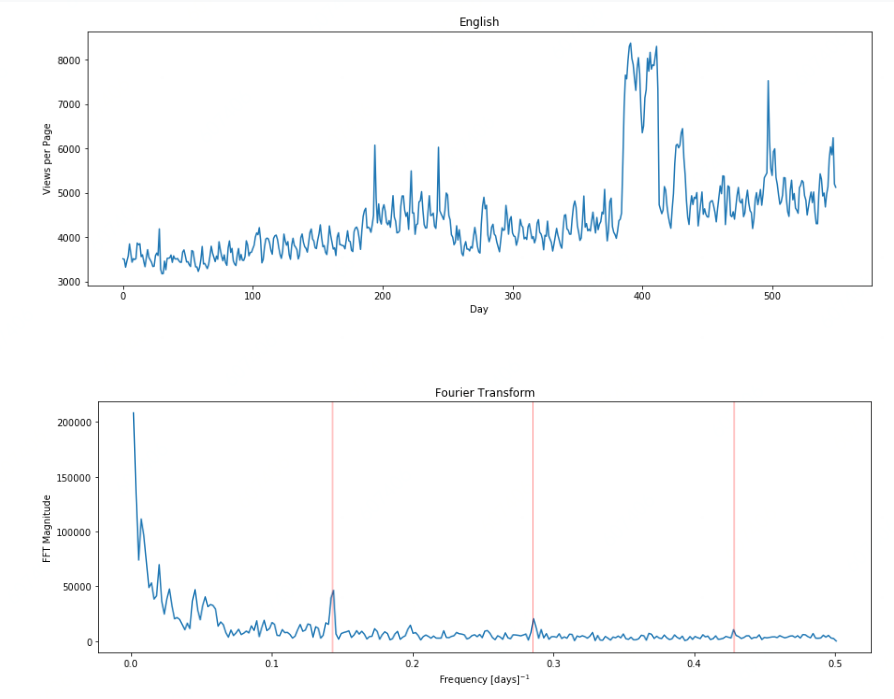
 上图是对图一中的英语国家进行FFT的结果，横坐标是频率/周期，红色实线是人为标注的结果（每隔7天画一条红线），纵坐标是FFT后结果的模（FFT的结果是一个复数，实部是频率、虚部是相位，它的模可以认为是FFT的能级、强度power）。

上图可以看出：该国家在7天为周期上表现得不是很强烈。

 

 

 

 

 

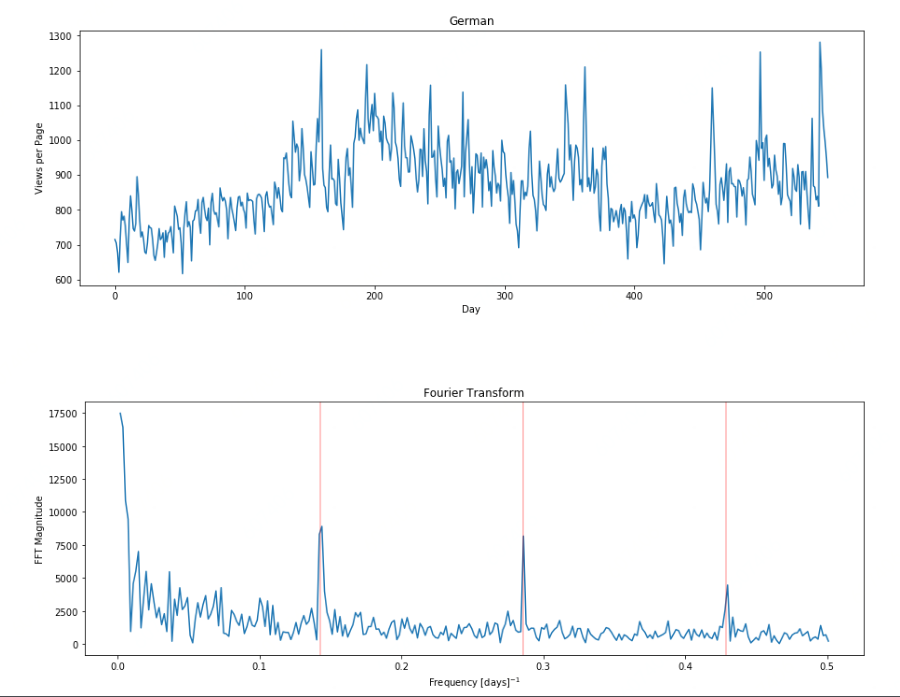
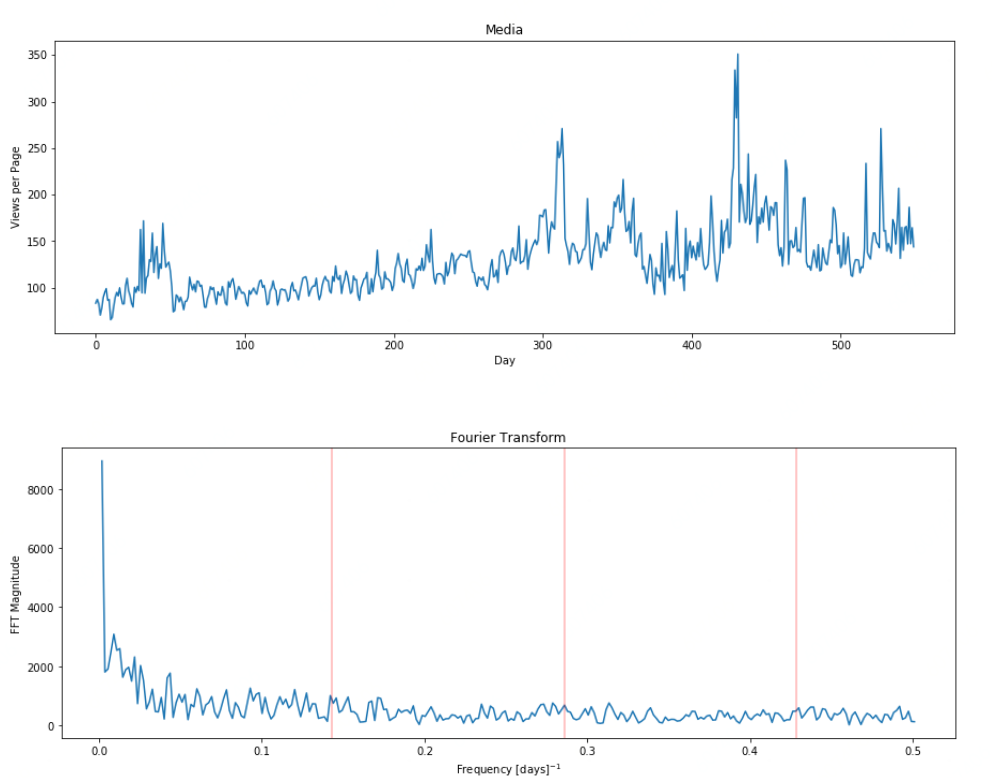
 由上图可以看出，德国在以7天为周期上有明显的特征，其他国家并不明显。