2. Equalibrium and Temperature

什么是Equalibrium (state)

Equalibirum state 可以说是系统演化的一个目标，当一个系统经过长时间的演化后处于一个与初始条件无关，且其一些宏观性质不随时间变化的状态时，我们就说系统进入了equalibrium state.

如何描述Equalibrium

实际上通过一组宏观上测量的量就可以描述equlibrium state了，但是这是静态的视角，我们希望从动态演化的视角来看，初衷是能不能通过动态的视角获得与所测的宏观性质一致的结论。为了从统计力学的角度来对系统的equalibrium state 进行描述，我们需要诉诸于以下的一些抽象模型

相空间(phase-space)

相 指的就是系统所处的状态，而相空间就是系统的状态空间。考虑一个只由一个三维空间的物体构成的系统，它的状态可以由它的位置(x,y,z)以及它的动量(\(p_x\),\(p_y\),\(p_z\))表达，那么这个物体的状态就是一个6维空间中的一个点\((x,y,z,p_x,p_y,p_z)\), 那么这个系统所处的所有状态都可以由这个6维空间中的点表达。现在再考虑有\(N\)个点构成的系统，现在描述一个这样的系统就需要6N个维度了，即\((x_1,y_1,z_1,p_1^x,p_1^y,p_1^z,\cdots,x_N,y_N,z_N,p_N^x,p_N^y,p_N^z)\) , 而现在系统的相空间就变成了6N维的空间了。所以相空间中的一个点就表示了系统所处的某个状态。

系综(ensemble)

假设我们研究的是系统\(A\), 当然系统\(A\)有不同的状态，现在我们按照某些确定的\(A\)的宏观性质(比如一定的总能量，温度，粒子数等)对\(A\)的所有微观状态进行归类，即处在这些确定的宏观性质下的所有微观状态取成一个集合，这个集合就是系综。

乍一看系综好像是具有一些相同宏观状态的微观态的集合，但这是从时间的角度来看的，即我们产生这样的想法是基于系统在不同时间下处于不同的微观状态的理念；但是这并不是我们定义系综的原因，也不是系综真正的定义。

系综实际上是系统的集合，集合中的元素是处于不同状态下的系统，这些系统具有相同的某些宏观性质，即这些处于不同状态下的系统之所以被划分为一个系综是因为我们按照某些确定的宏观性质来操作的。这个定义看上去和最开始的那种定义好像差不多，但是实际上这种定义实际上是从空间的角度来看待系综的，而这种角度牵涉到系综产生的原因。

对于一个\(N\)个粒子的系统，在给定一些初始条件的情况下，它演化到equlibrium state 需要经过一段相当长的时间，比如说你接了一杯热水然后放在桌上，it takes some time to cool down 冷却到室温(达到平衡(如果将屋子看做一个微正则系综的话))。现在我们需要测量和这个\(N\)粒子系统的一些宏观性质(比如一杯热水在室温下达到平衡的温度)，我们就需要等待一段它演化到平衡态的时间，在这段时间中，这个系统会经过若干个状态而达到平衡态，这就是从时间的角度来看，每个时间点对应一个系统的状态，系统的演化对应了相空间中的一条轨迹；而从空间的角度来看，假设我们能够看到系统演化的所有可能状态，我们就可以在某一个时刻将处于各个状态的系统都列出来(相空间中离散的点)，这样当我们需要测量这个系统处在平衡态的某些宏观特征时，我们只需要对这些各个状态的系统在这个宏观特征上取均值就可以了(可以证明这两种角度是等价的)。这里"各个状态的系统"的集合就是系综。

一个值得推敲的问题是宏观态和系综的关系，这个问题我在Physics Stackexchange上面看到了一些回答，但感觉都不是特别贴切。个人感觉宏观态的定义很主观，而微观态在系综确定了之后就很容易确定了。如果你定义宏观态是诸如温度，压强等可测的物理量，那其实在确定系综的时候固定这些物理量的同时就确定了宏观态，也就是说系综中的系统都具有这种宏观态；而如果你把一半粒子处于容器上半部，另一半处于下半部这种状态看做宏观态，那其实宏观态和系综就没啥关系了。

另外，关于系综和相空间的关系，某种程度上来说系综是相空间的子集。相空间中的一个点表示系统的一个状态，而系综中的一个元素表示的是处于某个状态的系统，虽然一个是系统所处的状态，另一个是处于某个状态的系统，但实际上一个微观态(相空间中)确实对应着一个系统(系综)，再加上系综实际上是满足某些宏观性质约束的系统的集合，所以系综从某种程度上看是相空间的子集，这个子集中的所有状态都满足某些宏观性质，而这进一步导致系综可以看做相空间这个高维空间中的一个曲面。

微正则系综

首先作为系综，微正则系综限制总能量以及总粒子数为定值来选择微正则系综中的系统，也就是说微正则系综中的每一个系统都具有相同的总能量以及总粒子数，这是微正则系综作为系综的一方面。另一方面，微正则表示该系综中的每一个系统(实际上是处于不同状态的同一个系统)都是isolated的，即不能和外界交换能量和粒子。

微正则系综中的一个重要的假设是微正则系综中处于不同状态的系统都具有同样的权重，不存在处于某个状态的系统备受青睐的情况。

关于微正则系综的讨论

下面的讨论主要是对于单原子的理想气体。假设有总能量为\(E\)，粒子数为\(N\)的理想气体放于体积为\(V\)的容器中，这个容器是密封且绝热的。因此这个容器中的理想气体可以被视为一个系统，而对应的处于不同状态下的系统的集合就是该理想气体的微正则系综了。每一个气体粒子可以通过其在三维空间中的位置，以及它每个方向上的动量来形式化，\(N\)个粒子所处的位置构成\(3N\)维的位型空间\(P\)(configuration space), 位型空间中每一个点表示这\(N\)个粒子的所有位置信息，同理得到这\(N\)个粒子所具有的动量就构成\(3N\)维的动量空间\(M\)(momentum space)。接下来我们就开始讨论在这个微正则系综下，粒子在位置空间和动量空间中的分布。需要说明的是，能够对粒子的位置和动量分开进行讨论的原因是理想气体满足能量和位置相互独立。

粒子的位置在位置空间中的分布

我们想要求的是\(\rho(\textbf{a})\)，其中\(\textbf{a} =(x_1,y_1,z_1,\cdots,x_N,y_N,z_N)\)。因为理想气体的位置和能量是相互独立的，也就是说总能量\(E\)下没有哪一个位置更受青睐，所以我们按照总能量\(E\)划分的微正则系综中各个系统的位置应该是同等的权重，也就是说\(\rho(\textbf{a})\)是一个常数，那么根据概率的归一性有

\(\rho\sum_{\textbf{a}}1 = 1\)

在大量粒子的情况下，上述式子可以写为积分的形式，而对应地，\(\rho\)也就成了概率密度，即

\(\rho\int dP = 1\)

进一步地，因为理想气体中粒子与粒子可以视为是相互独立的，所以有

\(\rho \int\int\cdots\int d(x_1,y_1,z_1)d(x_2,y_2,z_2)\cdots d(x_N,y_N,z_N) = 1\)

对于某个粒子\(k\)的\(\int d(x_k,y_k,z_k)\), 在高等数学这个积分表示在积分区域的"volume"(体积), 理想气体中的粒子在位置上只受制于处在体积为\(V\)的容器中，所以有\(\int d(x_k,y_k,z_k) = V\), 带入上述积分有

\(\rho V^N =1\)

即 $\rho = \frac{1}{V^N} $

粒子的动量在动量空间中的分布

粒子的动量在动量空间分布就要稍微复杂一点了，相对于求, \(\rho(\textbf{v})\), \(\textbf{v} = (p_1^x,p_1^y,p_1^z,\cdots,p_N^x,p_N^y,p_N^z)\), 我们更希望求粒子某个方向的动量\(\rho(p^x_i)\)在动量空间中的分布, 这个原因后面再解释。因为理想气体的能量独立于位置，所以理想气体的能量完全体现在其动能上面了，即

\(\sum_{i = 1}^{3N} \frac{p^2_i}{2m} = E\)

因为单原子的理想气体的\(m\)都相同，所以可以看到总能量为\(E\)的理想的气体的所有粒子的动量(系统的动量)分布在一个\(3N\)维空间的球面上(\(3N-1\) sphere，\(3N-1\)是这个球实际的维度，而不是它所在的空间的维度), 半径为\(\sqrt{2mE}\)：

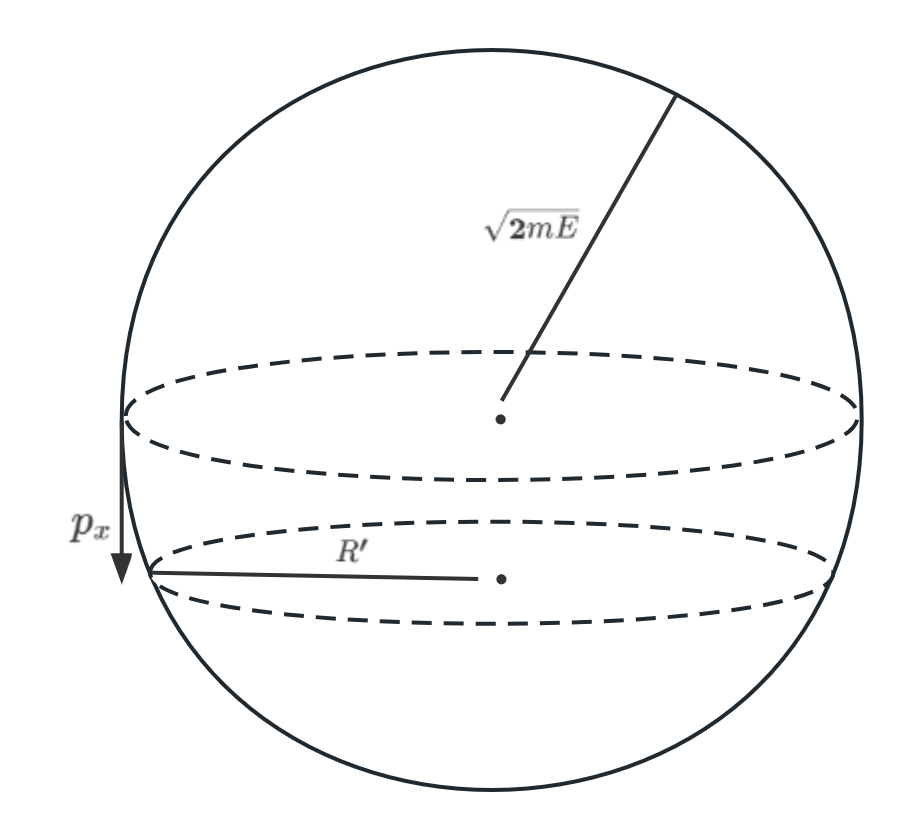
这个\(3N-1\)维球面上的每一个点给出了系统中所有粒子的一组可能的动量，所以这个\(3N-1\)球面就可以看做系统的动量空间(可以看做相空间)；而如果我们确定其中某个粒子的某个方向的动量, 如\(p_i^x\)后，整个动量空间就会塌缩到一个\(3N-2\)维球面，就像图中的那个半径为\(R' = \sqrt{2mE-(p_i^x)^2}\) 的"圆"一样，这个"圆"上的每一点给出了系统中所有粒子的一组\(p_i^x\)固定的动量。

为了求出\(\rho(p_i^x)\), 根据古典概型的思想，我们就需要求出\(3N-2\)维球上的点数与\(3N-1\)维球上的点数的比值。进一步地，根据几何概型的思想有

\(\rho(p_i^x) = \frac{V_{\sqrt{2mE}}^{3N-1}}{V_{\sqrt{2mE-(p_i^x)^2}}^{3N-2}}\)

其中\(V_R^d\)表示\(d\)维球面的体积，他可以通过高维球的体积公式求出

\(V_R^d = \frac{\pi^{(d+1)/2}R^{d+1}}{[(d+1)/2]!}\)

令\(R = \sqrt{2mE}\)可以得到

\(\rho(p_i^x) \propto \frac{R^2}{(R')^3}(\frac{R'}{R})^\frac{3N}{2}\)

根据等价无穷小有

\((\frac{R'}{R})^\frac{3N}{2} = (1-\frac{(p_i^x)^2}{2mE})^\frac{3N}{2}\sim e^{-\frac{(p_i^x)^2}{2m}\frac{3N}{2E}}\)

另一方面，\(R'\)与\(R\)甚为接近，所以

$ \frac{R^2}{(R')3} = \frac{1}{R'}\approx \frac{1}{\sqrt{2mE}}$

最终有

\(\rho(p_i^x) \propto \frac{1}{\sqrt{2mE}} e^{-\frac{(p_i^x)^2}{2m}\frac{3N}{2E}}\)

完事儿以后再根据概率密度的归一性可以得到

\(\rho(p_i^x) = \frac{1}{\sqrt{2\pi m(2E/3N)}} e^{-\frac{(p_i^x)^2}{2m}\frac{3N}{2E}}\)

可以粒子的某个动量在动量空间中一个高斯分布，其中\(\mu = 0, \sigma = \sqrt{\frac{2mE}{3N}}\)。 这个高斯分布告诉我们对于那些某个方向动量很大的粒子(动能很大)，它们的数量很少。

现在我们通过刚刚介绍的这些概念通过一些macrosopic properties来描述equalibrium states. 这些macroscopic properties 是温度，压强以及化学势(chemical potential)

温度，压强以及化学势的统计力学定义

考虑一个体积为\(V\)的绝热箱子里面装着总能量为\(E\)的有着\(N\)个粒子的气体，我们把这个箱子看做两个体积分别为\(V_1\)和\(V_2\)以及对应的能量分别为\(E_1\)和\(E_2\)的子系统，体积为\(V_1\)的子系统的温度为\(T_1\), 而体积为\(V_2\)的子系统的温度为\(T_2\)。

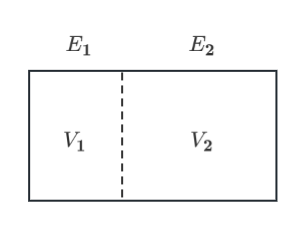
温度的定义

对于上述系统，一个常识就是经过一段时间后，两个子系统的温度会稳定到一个数值，整个系统呈现一个温度，纵然温度通过我们的感官很好感知，但我们还是要问当我们讨论温度的时候，我们究竟在讨论什么？实际上从这个常识中我们知道，如果运用统计力学的方法能够得到一个指标，而上述的两个系统在这个指标下是相等的，那这个指标就可以作为温度的一个定义。现在我们从子系统的相空间出发，对于#1子系统，在它的能量为\(E_1\)的限制之下，它的相空间实际上是一个曲面，所以相空间的体积实际上是这个曲面的表面积，但是这个曲面不像上面的动量空间那样是一个高维球面，这个曲面可能是不规则的，所以它的表面积不好直接求，我们可以利用积分求体积的方法再除以一个厚度(高)来求得表面积，即考虑能量为\(E\)和\(E+\delta E\)构成的体的体积

\(V_{E,\delta E} = \int_{E_1<H_1<E_1+\delta E} dPdQ = \int \Theta(E_1+\delta E-H_1)-\Theta(E_1-H_1)dPdQ\)

这里\(H\)是哈密顿量，\(\Theta(x)\)是单位阶跃函数。这是一个厚度为\(\delta E\)的体，当\(\delta E\)足够小时，#1的相空间的体积(也就是曲面的表面积)\(\Omega_1(E_1)\)可以写为

\(\Omega_1(E_1) = \frac{V_{E,\delta E}}{\delta E} = \frac{1}{\delta E}\int \Theta(E_1+\delta E-H_1)-\Theta(E_1-H_1)dPdQ\)

进一步地根据微分的定义以及单位阶跃函数的导数是\(\delta\)函数(突变的导数是正无穷)可以得到

\(\Omega_1(E_1) = \int \frac{d\Theta(E_1-H_1)}{dE}dPdQ = \int \delta(E_1-H_1)dPdQ\)

同理可得\(\Omega_2(E_2)\)的相空间体积。\(\Omega_1(E_1)\)可以理解为是所有能量为\(E\)(\(\delta E\)很小)的系统的个数，所以对于整个系统来说，某个特定的能量\(E_1\)下所有能量为\(E = E_1+E_2\)的系统的个数\(\Omega_1(E_1)\Omega_2(E-E_1)\), 然后对所有可能的\(E_1\)进行求和(积分)，最后我们可以得到整个系统的相空间\(\Omega(E)\), 它描述了所有总能量为\(E\)的系统

\(\Omega(E) = \int \Omega_1(E_1)\Omega_2(E-E_1) dE_1\)

这里我们可以把\(\Omega(E)\)除过去，然后得到

\(\rho(E_1) = \frac{\Omega_1(E_1)\Omega_2(E-E_1)}{\Omega(E)}\)

根据\(\rho(E_1)\)的积分为1，且\(\rho(E_1)\geq 0\)， 我们可以将\(\rho(E_1)\)看做是一种密度，它描述了子系统1处于某个特定的能量\(E_1\)以及子系统2处于能量\(E-E_1\)下的概率(密度)

这里我们停一下，来思考一下这个系统在平衡态(equalibrium)应该是什么样的，上面已经说过了，在equlibrium时，我们可以首先觉察到的是两个子系统的温度应该是一样的，假设此时子系统1的能量是\(E_1^*\), 也就是说此时子系统1处于能量\(E_1^*\)的状态的概率最大(可以想象成概率密度函数在\(E_1^*\)处有一个尖峰)，并且处于其他能量下的概率很小(可以看做小概率事件)，这也就是说\(E_1^*\)使得\(\Omega_1(E_1)\Omega_2(E-E_1)\)最大，我们对它求导并令其为0可以得到

\(\frac{1}{\Omega_1}\frac{d\Omega_1}{dE_1}|_{E_1 = E_1^*} = \frac{1}{\Omega_2}\frac{d\Omega_2}{dE_2}|_{E_2 = E-E_1^*}\)

实际上对于这个式子，微积分在线的同学可以看到有

\(\frac{d\ln\Omega_1}{dE_1}|_{E_1 = E_1^*} = \frac{d\ln\Omega_2}{dE_2}|_{E_2 = E-E_1^*}\)

现在我们终于得到了在平衡时我们希望得到的两个子系统相等的量了，它表示当总能量为\(E\)时，如果子系统1分得能量\(E_1^*\), 子系统2分得能量\(E-E_1^*\), 那么这种能量分配方式会被称为“处于相同的温度”，所以有

\(\frac{1}{T} = k_B\frac{d\ln \Omega}{d E}\)

多一个玻尔兹曼常数是因为熵的定义有

\(S_{equil}(E) = k_B log(\Omega(E))\)

所以上式更简单地写为

\(\frac{1}{T} = \frac{dS}{dE}\)

这个式子告诉我们，如果我们从外界吸收了\(d E\)的能量，我们自身会熵增\(dS\)，而外界则会熵减\(dS\).

压强以及化学势的定义

还是上面那个系统，对于熵的定义式，for completeness, 它应该被写成

\(\frac{1}{T} = \frac{dS}{dE}|_{V,N}\)

这个式子表示温度的定义应该限制在一定的volume(V)以及粒子数目下，它表示熵如何随着能量变化。那熵如何随着volume(V)和粒子数变换呢？我们看熵的全微分\(\Delta S\)

\(\Delta S = \Delta S_1+(-\Delta S_2)\)

这里我们将熵看做是正数，所以对于两个子系统中的其中一个系统，它应该是熵减的。

根据全微分的定义有

\(\Delta S_1 = \frac{\partial S_1}{\partial E_1}\Delta E_1+\frac{\partial S_1}{\partial V_1}\Delta V_1+\frac{\partial S_1}{\partial N_1}\Delta N_1\)

\(\Delta S_2 = \frac{\partial S_2}{\partial E_2}\Delta E_2+\frac{\partial S_2}{\partial V_2}\Delta V_2+\frac{\partial S_2}{\partial N_2}\Delta N_2\)

其中\(\Delta E\), \(\Delta V\)以及\(\Delta N\)表示两个系统间的微小的能量，体积以及粒子数的改变量

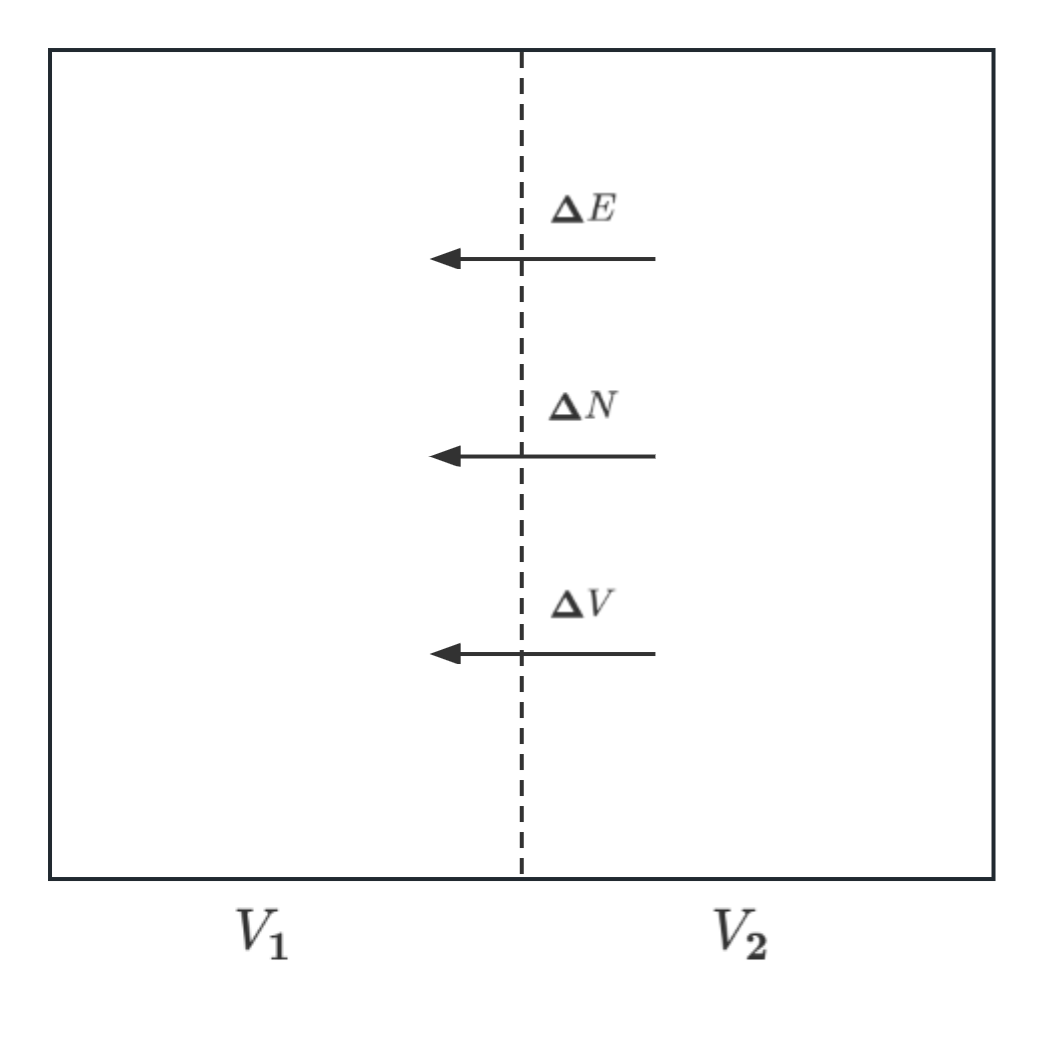
这里就有

\(\Delta S = \biggl(\frac{\partial S_1}{\partial E_1}|_{V,N}-\frac{\partial S_2}{\partial E_2}|_{V,N}\biggr)\Delta E+\biggl(\frac{\partial S_1}{\partial V_1}|_{E,N}-\frac{\partial S_2}{\partial V_2}|_{E,N}\biggr)\Delta V+\biggl(\frac{\partial S_1}{\partial N_1}|_{V,E}-\frac{\partial S_2}{\partial N_2}|_{V,E}\biggr)\Delta N\)

和温度的定义一样，我们可以对上述式子进行如下定义

\(\frac{P}{T} = \frac{\partial S}{\partial V}|_{E,N}\)

\(-\frac{\mu}{T} = \frac{\partial S}{\partial N}|_{E,V}\)

其中\(P\)就是压强，而\(\mu\)就是化学势。可以看到当两个子系统的温度，压强，化学势都相等时，整个系统就进入了平衡态，此时有\(\Delta S = 0\)，也就是说对于isolated的系统，它演化到平衡态时熵不再变化。

理想气体方程

根据熵的定义

\(S = k_B \log(\Omega(E))\)

总系统的相体积\(\Omega(E)\)等于位型空间的相体积乘以动量空间的相体积，在上面我们已经求得了位型空间的相体积为\(V^N\), 而动量空间的体积根据高维球的体积公式(除以厚度\(\delta E\))可以得到, 那么有

$\Omega(E) = $$V^N (\frac{3N}{2E})\frac{\pi^{3N/2}2mE{3N/2}}{(3N/2)!}$

那么整个系统的熵为

\(S_{crude}(E) = N_{kB}\log(V)+\frac{3Nk_B}{2}(2\pi mE)-k_B\log[(\frac{3N}{2})!]+C\)

所以分别对\(E\)和\(V\)求导给出

\(\frac{\partial S}{\partial E}|_{V,N} = \frac{3Nk_B}{2E} = \frac1T\)

\(\frac{\partial S}{\partial V}|_{E,N} = \frac{Nk_B}{V} = \frac{P}{T}\)

上述两个式子给出

\(k_BT = \frac{2E}{3N}\)

\(PV = Nk_BT\)

而第二个式子便是isolated的系统的理想气体方程。