重温DFS与BFS算法（一）

       最近在看蓝桥杯的题目，看见2019年B组E题的迷宫题，想到使用BFS来求解，但又遗忘了DFS与BFS的知识，哎不得不重新学过。

       好开始正题。

       数据结构在对图进行遍历时，使用到DFS与BFS。什么是DFS与BFS呢？

      深度优先搜索）：在图中取一点开始，从这一点寻找与它关联的点，在从新找的这一点开始，继续找下一点。遍历过的点均需标记，防止重复遍历，在DFS中运用了回溯，当遍历这一点的一条分支结束后，没有更深的点便回溯到这一点上，遍历令一分支，直到遍历完这一个图的连通分量。

      BFS（广度优先搜索）：在图中取一点开始，运用到队列的知识，将这点点标记，并将其所有子节点入队列，访问队列首元素将其所有子节点入队列，将次首元素出队列，并访问队列下一元素，重复此过程，直到队列为空为止。即表示该图的一个联通分类已完全遍历。

       

     DFS回溯：

     回溯法是一种搜索法，按条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法；

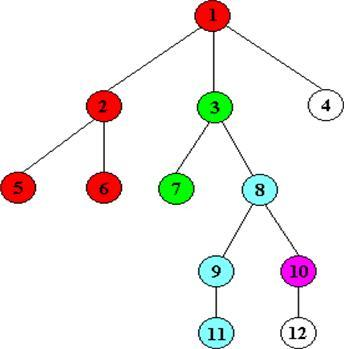
例如这张图，从1开始到2，之后到5，5不能再走了，退回2，到6，退回2退回1，到3，一直进行；

 

 

 

      BFS的队列

一张图，bfs就是和它类似，很好的帮助理解，雷从上往下，同时向四面八方的延长（当然不是很严谨的），然后找到那个最近的建筑物，然后劈了它；

还是这张图，从1开始搜，有2，3，4几个点，存起来，从2开始有5，6，存起来，搜3，有7，8，存起来，搜4，没有了；现在开始搜刚刚存的点，从5开始，没有，然后搜6.。。一直进行，直到找到；

 

 

代码如下：（采用了刚学习数据结构时的代码十分简陋但是便于理解算法含义）

 

 

1邻接矩阵DFS分析

(1)设计标记数组将访问过的顶点标记为1(2)访问结点v，并标记为1(3)for循环从顶点v开始遍历，从0到n若从v到j有边，且j顶点未被标记，则以j为顶点递归DFS

代码

//邻接矩阵下从v出发深度优先遍历图递归算法DFS
int visited[MaxSize];      //为全局标志数组
void MGraph::DFS(int v)
{
int n=vertexNum;
if(v>=n||v<0)
     {cout<<"位置出错";
      return;
     }
cout<<vertex[v]<<" ";   //访问顶点
visited[v]=1;           //标记
for(int j=0;j<n;j++)
if(adj[v][j]==1&&visited[j]==0)
DFS(j);                                   //单连通图顶点可全部遍历 
}

 

 

 

 

 

邻接矩阵BFS分析

(1)设计标记数组，构建队列Q(2)访问顶点v，标记为1，v入队列(3)当队列不为空时while()(4)访问栈顶元素并出队列，用for循环遍历，将所有与栈顶顶点有边且未标记的顶点j入队列，并标记

代码

//采用邻接矩阵从v广度优先遍历图的算法BFS
void MGraph::BFS(int v)
{ int n=vertexNum;int front,rear;              //队列头尾
  if(v>=n||v<0){cout<<"位置出错";return;}
  int Q[MaxSize];                              //Q作为队列 顺序队列
  front=rear=-1;
  cout<<vertex[v]<<" ";
  visited[v]=1;
  Q[++rear]=v;                                //被访问顶点入队
  while(front!=rear)                          //队非空
  { v=Q[++front];                       //将对头元素出队并送到v中
    for(int j=0;j<n;j++)                  //for循环完成将v的所有边连接的结点送入队列 
if(adj[v][j]==1&&visited[j]==0)
{ cout<<vertex[j]<<" ";
  visited[j]=1;
  Q[++rear]=j;                            //入队列 
}
  }
}

 

 

 

 

 

2邻接表DFS分析

(1)设计标记数组(2)访问顶点v，并标记(3)从顶点v出发，边结点指针p指向顶点v第一个结点(4)当p不为NULL时，while循环，若边结点中顶点j未访问则递归DFSL(j)，在while循环后p指向下一结点

//邻接表表示从v出发深度优先遍历图递归算法DFSL
//前面已构建好顶点结点与边表结点 
void ALGraph::DFSL(int v)
{
int n=vertexNum;ArcNode *p;int j;  //ArcNode *p;为边表结点指针
if(v>=n||v<0){cout<<"位置错误";return;}
cout<<adjlist[v].vertex<<" ";
 visited[v]=1;
 p=adjlist[v].firstedge;
 while(p)
 {   j=p->adjvex;
     if(visited[j]==0)DFSL(j);
     p=p->next;            //单联通的返回商议结点操作 
 }
}

 

 

 

 

 

邻接表BFS分析

(1) 标记数组visited[]，队列Q，初始化标记数组和队列(2)访问顶点v，标记顶点v，并将v入队列。(3)当队列不为空时while循环，取栈顶顶点，边顶点指针指向，栈顶顶点第一个边结点，将单链表中未被访问的顶点访问，并标记，再存入队列中(4)while循环中p=p->next

(2) 

//从邻接表下从v广度优先搜索遍历图的算法BFSL
void ALGraph::BFSL(int v)
{ int n=vertexNum;
  if(v>=n||v<0){cout<<"位置出错";return;}
  int front,rear;ArcNode *p;                  //ArcNode *p;为边表结点指针
  int Q[MaxSize];
  front=rear=-1;
  cout<<adjlist[v].vertex<<" ";
  visited[v]=1;Q[++rear]=v;
  while(front!=rear)
  { v=Q[++front];
    p=adjlist[v].firstedge;
    while(p)
    {   j=p->adjvex;
        if(visited[j]==0)
        { cout<<adjlist[j].vertex<<" ";
          visited[j]=1;
          Q[++rear]=j;
        }
        p=p->next;                    //重要 
    }
  }
}

 

 

 

关于DFS的回溯图解与BFS的队列图解转自  https://www.cnblogs.com/wzl19981116/p/9397203.html

 

 

 

 

                                                                                                                                                                                                                                                                                                                        2020-03-22  21:08:11