花落--HashMap系列之1.8TreeNode删除源码篇(四)
嗨,同学们又见面了,小宋在前面hashmap的系列文章中我们依次从1.7讲到了1.8的树化,下面我会接着上篇文章的树化源码TreeNode接着往下讲,今天讲的是TreeNode的删除源码分析。
TreeNode删除
上篇文章的树化源码是分了两步来走的(treeify到balanceInsertion),同样TreeNode删除节点也是两步走(removeTreeNode到balanceDeletion),先进行二叉查找树的删除,然后再进行红黑树的调整,跟之前的情况分析是一致的。
removeTreeNode函数
public V remove(Object key) {
Node<K,V> e;
return (e = removeNode(hash(key), key, null, false, true)) == null ?
null : e.value;
}
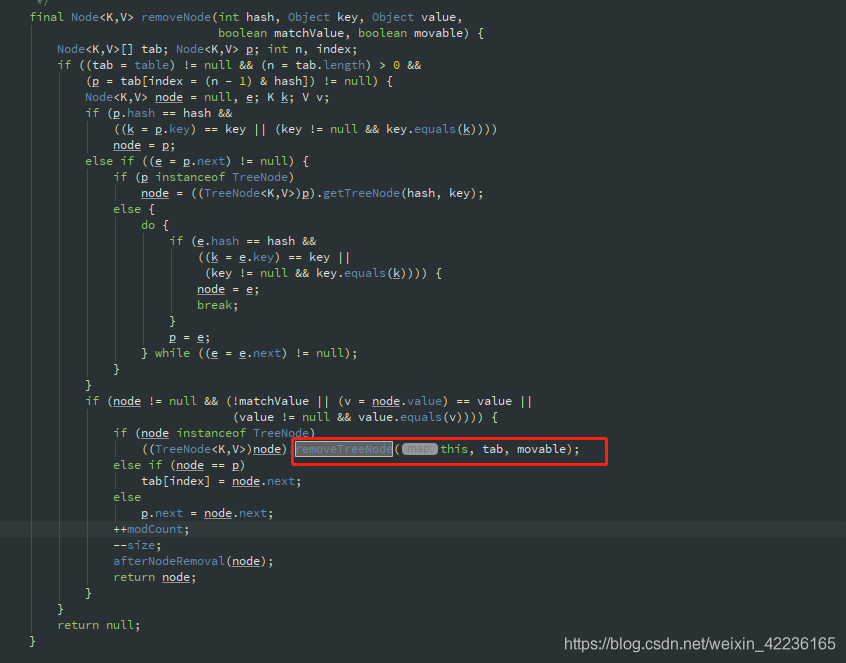
从remove函数内部的removeNode往下走到removeTreeNode
/**
* Removes the given node, that must be present before this call.
* This is messier than typical red-black deletion code because we
* cannot swap the contents of an interior node with a leaf
* successor that is pinned by "next" pointers that are accessible
* independently during traversal. So instead we swap the tree
* linkages. If the current tree appears to have too few nodes,
* the bin is converted back to a plain bin. (The test triggers
* somewhere between 2 and 6 nodes, depending on tree structure).
* 移除给定的节点,这个方法相比一般的红黑树删除更加杂乱,因为我们无法交换内部节点的内容他们被next指针给限制了,这个指针是在遍历的时候独立的。
* 因此我们交换树的连接。如果当前的树节点太少,需要转换为线性链表,通常这个值设定为2-6个节点
*/
final void removeTreeNode(HashMap<K,V> map, Node<K,V>[] tab,
boolean movable) {
int n;
if (tab == null || (n = tab.length) == 0)
return;
int index = (n - 1) & hash;//index = hash mod n
TreeNode<K,V> first = (TreeNode<K,V>)tab[index], root = first, rl;
TreeNode<K,V> succ = (TreeNode<K,V>)next, pred = prev;//succ指向要删除节点的后一个点(next后一个节点),pred指向要删除节点的前一个(prev前一个节点)
if (pred == null)
tab[index] = first = succ;//若要删除的节点的前一个为空,则first和tab[index]都指向要删除结点的后一个结点
else
pred.next = succ;//若要删除结点的前驱非空,则前一个结点的next指针指向该节点的后驱
if (succ != null)
succ.prev = pred;//后驱节点不为空时,后驱节点的前置指针设为删除节点的前置节点
if (first == null)
return;//若删除的节点是树中的唯一结点则直接结束
if (root.parent != null)
root = root.root();//确保root指向根结点
if (root == null || root.right == null ||
(rl = root.left) == null || rl.left == null) {
tab[index] = first.untreeify(map); // 根自身或者左右儿子其中一个为空说明结点数过少(不超过2)转为线性表并结束
return;
}
TreeNode<K,V> p = this, pl = left, pr = right, replacement;//p指向要删除的结点,pl指p的左子节点,pr指p的右子节点,replacement用于后续的红黑树调整,指向的是p或者p的继承者。
if (pl != null && pr != null) {
TreeNode<K,V> s = pr, sl;
while ((sl = s.left) != null) //删除节点的左右节点都不为空时,寻找右子树中最左的叶结点作为后继,s指向这个后继节点
s = sl;
boolean c = s.red; s.red = p.red; p.red = c; //交换后继节点和要删除节点的颜色
TreeNode<K,V> sr = s.right; //s后继节点的右子节点
TreeNode<K,V> pp = p.parent; //p要删除节点的父节点
if (s == pr) {
p.parent = s;//p是s的直接父亲,交换p和s的位置
s.right = p;
}
else {
TreeNode<K,V> sp = s.parent;
if ((p.parent = sp) != null) {
if (s == sp.left) //s在sp父节点的左节点
sp.left = p;//p放到s原本的位置
else //s在sp父节点的右节点
sp.right = p; //p放到s原本的位置
}
if ((s.right = pr) != null) //p的右子树节点成为s的右子树节点
pr.parent = s;//s放到p原本的位置
}
p.left = null;
if ((p.right = sr) != null)//s原本的右子树成为p的右子树
sr.parent = p;//p放到s原本的位置
if ((s.left = pl) != null) //p原本的左子树成为s的左子树
pl.parent = s; //s放到p原本的位置
if ((s.parent = pp) == null) //s的父节点为p的父节点是null
root = s;//若s原本是根则新的根是s
else if (p == pp.left)
pp.left = s;//若p是某个节点的左节点,则s成为该节点的左节点
else
pp.right = s;//若p是某个节点的右节点,则s成为该节点的右节点
if (sr != null)//若s节点有右节点(s一定没有左节点),则replacement为这个右节点否则为p
replacement = sr;
else
replacement = p;
}
else if (pl != null)//若p的左右节点有一方为null,则replacement为非空的一方,否则为p自己
replacement = pl;
else if (pr != null)
replacement = pr;
else
replacement = p;
//如果p是叶子节点,replacement==p,否则replacement为p的右子树中最左节点
if (replacement != p) {//p有子节点或者s有子节点
//若p不是叶子节点,则让replacement的父节点指向p的父节点
TreeNode<K,V> pp = replacement.parent = p.parent;
if (pp == null)//用replacement来替换p
root = replacement;
else if (p == pp.left)
pp.left = replacement;
else
pp.right = replacement;
p.left = p.right = p.parent = null;//移除p结点
}
//以replacement为中心,进行红黑树性质的修复,replacement可能为s的右节点或者p的子节点或者p自己
TreeNode<K,V> r = p.red ? root : balanceDeletion(root, replacement);
if (replacement == p) { //p没有子节点或者s没有子节点,直接移除p
TreeNode<K,V> pp = p.parent;
p.parent = null;
if (pp != null) {
if (p == pp.left)
pp.left = null;
else if (p == pp.right)
pp.right = null;
}
}
if (movable)
moveRootToFront(tab, r);//整理根结点
}
下面是删除节点后红黑树的调整修复,balanceDeletion。有点复杂,得有点耐心,继续往下看具体实现。
balanceDeletion函数
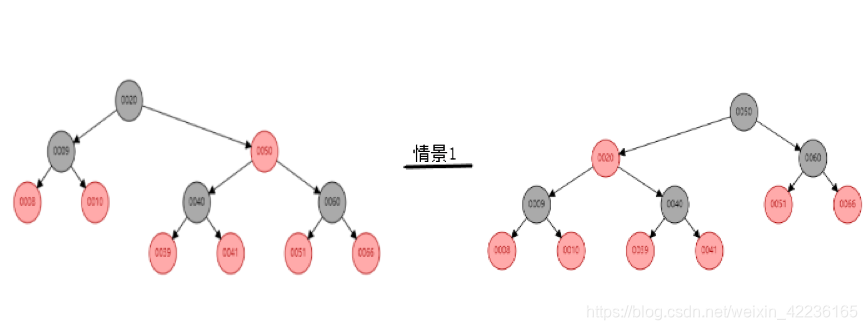
图解如下(第一张图在专业工具画的,后面的回家赶时间就直接拿流程图画了)😂
static <K,V> TreeNode<K,V> balanceDeletion(TreeNode<K,V> root,
TreeNode<K,V> x) {
for (TreeNode<K,V> xp, xpl, xpr;;) {
if (x == null || x == root)
return root;//删除节点为空或者删除的是根节点,直接返回
//x为根节点,染成黑色,直接返回(因为调整过后,root并不一定指向删除操作过后的根节点,如果之前删除的是root节点,则x将成为新的根节点)
else if ((xp = x.parent) == null) {
x.red = false;//删除后x成为根节点,x的颜色改为黑色
return x;
}
//如果x为红色,则变色,返回
else if (x.red) {
x.red = false;//将一个红色的节点变黑提升到删除节点的位置不会改变黑高
return root;
}
else if ((xpl = xp.left) == x) {//x是xp(父节点)的左子节点
if ((xpr = xp.right) != null && xpr.red) { //xp(父节点)的右子节点xpr不是null而且是红色的,同时它的父亲节点xp一定是黑色节点
//情景1,x的兄弟是红色的,x现在是xp的左子节点xpl,xpr现在是红色的。
xpr.red = false; //将xpr设置为黑色
xp.red = true; //xp设置为红色
root = rotateLeft(root, xp); //对父节点xp左旋(rotateLeft的源码解析在上个章节中)
xpr = (xp = x.parent) == null ? null : xp.right; //重新将xp指向x的父节点,xpr指向xp新的右子节点
}
if (xpr == null)
x = xp;//若x没有兄弟,xpr为空,向上继续调整,x上升到父亲的位置,将x的父节点xp作为新的x继续循环
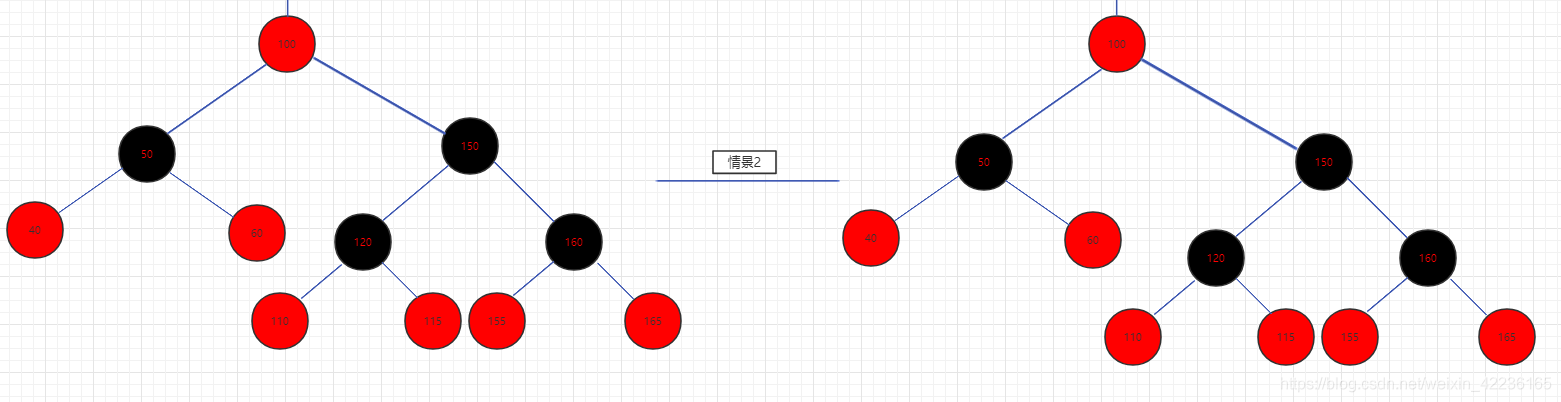
else {
//sl和sr是x兄弟的左子节点和右子节点
TreeNode<K,V> sl = xpr.left, sr = xpr.right;
if ((sr == null || !sr.red) &&
(sl == null || !sl.red)) {
//情景2,x兄弟是黑色,他的两个儿子是黑色的或者不存在
xpr.red = true;//因为xpr没有红色的子节点,违反了黑色高度,所以将xpr染红
x = xp; //本轮结束继续向上循环
}
else { //否则的话,就需要进一步调整
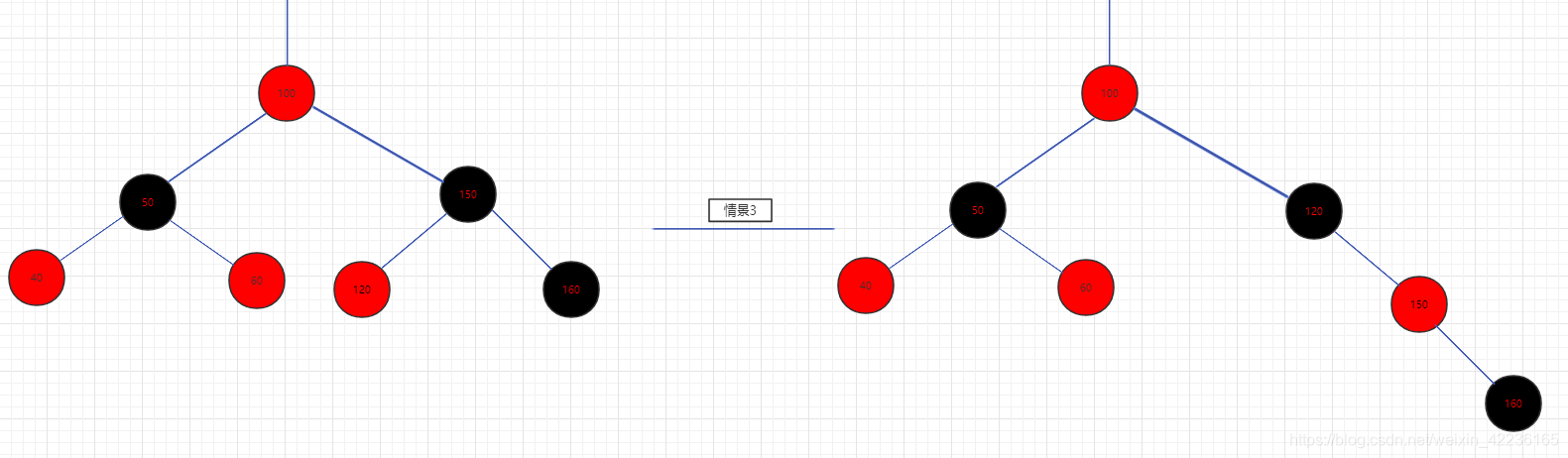
//情景3:x兄弟是黑色,他的右子节点不存在或者为黑色,左子节点是红色
if (sr == null || !sr.red) {
if (sl != null) //若左子节点存在为红,右孩子不存在或为黑
sl.red = false; //将左子节点染黑
xpr.red = true; //将x的兄弟xpr染红
root = rotateRight(root, xpr); //对x的兄弟xpr右旋
xpr = (xp = x.parent) == null ?
null : xp.right; //右旋完后,xpr指向xp的新右子节点,即上一步中的sl
}
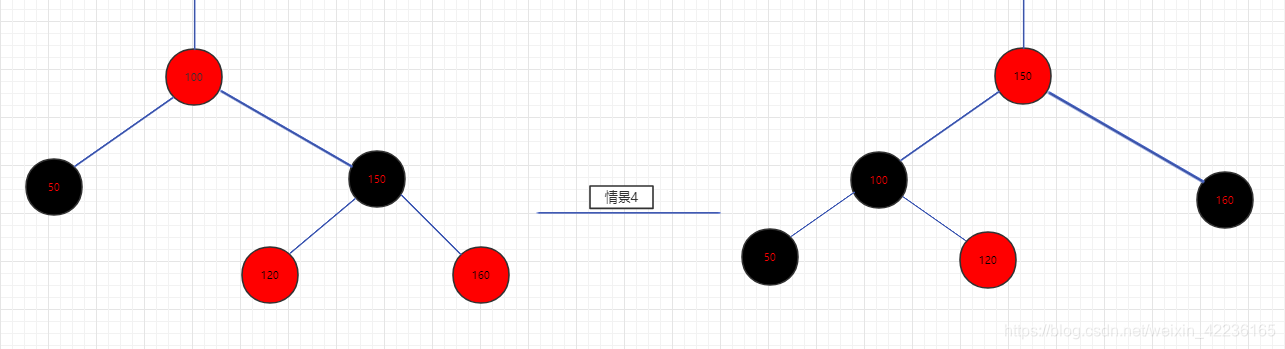
//情景4
if (xpr != null) {
xpr.red = (xp == null) ? false : xp.red; //xpr染成跟父节点一致的颜色,为后面父节点xp的左旋做准备
if ((sr = xpr.right) != null)
sr.red = false; //xpr新的右子节点染黑,防止出现两个红色相连
}
if (xp != null) {
xp.red = false;//将xp染黑,并对其左旋,这样就能保证被删除的X所在的路径又多了一个黑色节点,从而达到恢复平衡的目的
root = rotateLeft(root, xp);//对xp进行左旋
}
//到此调整已经完毕,进入下一次循环后将直接退出
x = root;
}
}
}
//上面说的是x为xp(父节点)的左子节点,现在作为右子节点,以下是对称操作
else {
if (xpl != null && xpl.red) {
xpl.red = false;
xp.red = true;
root = rotateRight(root, xp);
xpl = (xp = x.parent) == null ? null : xp.left;
}
if (xpl == null)
x = xp;
else {
TreeNode<K,V> sl = xpl.left, sr = xpl.right;
if ((sl == null || !sl.red) &&
(sr == null || !sr.red)) {
xpl.red = true;
x = xp;
}
else {
if (sl == null || !sl.red) {
if (sr != null)
sr.red = false;
xpl.red = true;
root = rotateLeft(root, xpl);
xpl = (xp = x.parent) == null ?
null : xp.left;
}
if (xpl != null) {
xpl.red = (xp == null) ? false : xp.red;
if ((sl = xpl.left) != null)
sl.red = false;
}
if (xp != null) {
xp.red = false;
root = rotateRight(root, xp);
}
x = root;
}
}
}
}
}
讲到这里应该对TreeNode删除的源码都了解了,如果想了解hashMap其他知识的可以看之前的系列文章,谢谢大家的观看,希望能给各位同学带来帮助。如果觉得博主写的还可以的,可以点赞关注。😉



 浙公网安备 33010602011771号
浙公网安备 33010602011771号