贝塞尔曲线

背景#

贝塞尔曲线在计算机图形学中的应用十分广泛，photoshop的钢笔工具，字体的轮廓，以及各种需要描述轨迹的地方如摄像机轨迹，粒子的速度曲线都用到了贝塞尔曲线。

贝塞尔曲线的数学基础——伯恩斯坦多项式（可以理解为：一个连续函数，可以将它表示成n个伯恩思坦多项式相加的形式，并且随着n 趋向于无穷大，这个多项式将收敛到原函数）建立于 1912 年，但直到1959 年，数学家 Paul de Casteljau 发明出数值稳定的 de Casteljau 算法时，多项式才应用于图形。de Casteljau 算法在法国获得了专利，但直到 80 年代才公布，而贝塞尔多项式在 1960 年代被法国工程师皮埃尔·贝塞尔（Pierre Bézier）应用于雷诺汽车的车身设计，并得到广泛宣传。

这个网页能模拟钢笔工具的应用：bezier.method.ac/。

贝塞尔曲线公式#

给定一系列控制点，第一个和最后一个控制点为贝塞尔曲线的起点和终点，并且由中间的控制点控制曲率。

下面推导一下贝塞尔曲线的公式。给定n个控制点$P_0$、$P_1$……$P_n$，求贝塞尔曲线$B(t)$，$t \in[0, 1]$。

根据控制点的个数，可以将贝塞尔曲线分类为不同阶数，从一阶曲线推广到多阶，可以快速理解贝塞尔曲线的计算。

一阶贝塞尔曲线（2个控制点）#

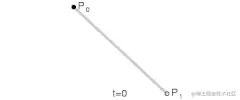
这是一条线段，很容易得到曲线的公式

$B(t) = P_0 + (P_1- P_0) t = (1-t)P_0 + tP_1$

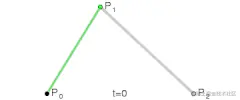
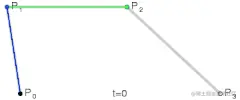
二阶贝塞尔曲线（3个控制点）#

先在三个控制点组成的两条线段$P_0P_1$、$P_1P_2$，上用一阶贝塞尔曲线公式求出新的控制点$Q_0$、$Q_1$，再对这两个新的控制点运用一阶公式，得到的新的点就是贝塞尔曲线在$t$的值。

$Q_0 = (1-t)P_0 + tP_1$

$Q_1 = (1-t)P_1 + tP_2$

$B(t) = (1-t)Q_0 + tQ_1 = (1-t)^2P0 + 2(1-t)tP_1 + t^2P_2$

三阶贝塞尔曲线（4个控制点）#

类似于二阶贝塞尔曲线的推导，

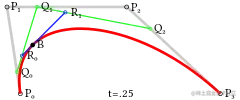
先求出一系列控制点$Q_0$、$Q_1$、$Q_2$。

$Q_0 = (1-t)P_0 + tP_1$

$Q_1 = (1-t)P_1 + tP_2$

$Q_3 = (1-t)P_2 + tP_3$

再求出新的控制点$R_0$、$R_1$，

$R_0 = (1-t)R_0 + tR_1$

$R_1 = (1-t)Q_1 + tQ_2$

可得贝塞尔曲线的公式，

$B(t) = (1-t)R_0 + tR_1 = (1-t)^3P_0 + 3t(1-t)^2P_1 + 3t^2(1-t)P_2 + t^3P_3$

n阶贝塞尔曲线（n+1个控制点）#

推广到n阶，可得

$B(t) = \sum_{N=0}^{n} C_n^iP_i(1-t)^{n-i}t^i$

以上就是De Casteljau算法的思想，通过递归求控制点，求得贝塞尔曲线。

参考#

1. en.wikipedia.org/wiki/B%C3%A…
2. 深入理解贝塞尔曲线 - 掘金