压缩感知的应用
压缩感知的应用
在上一期文章中,我们介绍了压缩感知( CS)的基本概念、理论基础、稀疏性和不可压缩性等内容。本期我们探讨压缩感知在信号处理中的数据恢复应用,演示压缩感知的信号采集与重建过程。
信号处理中的数据恢复
在许多信号处理应用中,例如地震信号的分析,往往由于传感器的限制导致采样不完整。压缩感知技术可以通过稀疏信号重建的方法,恢复缺失的数据,使得我们能够重建原始信号,从而提高分析的准确性。
在地震信号处理中,地震仪器通常无法在所有位置和时间对地震活动进行全面采样,这就导致信号数据不完整。而通过压缩感知,我们可以利用地震信号在特定变换域中的稀疏性来重建丢失的数据。这种数据恢复能力在地震勘探、油气勘测以及地质监测等领域具有重要应用,可以帮助专家更好地分析地层结构和地震活动。
例如,在油气勘探中,地震波信号往往是稀疏的,即只有少数几个反射信号包含有用信息,其余大部分为噪声。压缩感知通过减少对这些噪声的采样,并聚焦于有用信号的采集,使得勘探工作变得更加高效。此外,通过压缩感知重建技术,我们可以在数据缺失的情况下重建地震反射信号,这对于减少成本和提高采样效率至关重要。
压缩感知的理论基础依赖于信号的稀疏性和测量矩阵的不可压缩性。在地震信号处理中,地震信号在特定基下具有稀疏性,例如在小波变换域中,地震反射信号可以用少量的非零系数表示。因此,我们可以通过较少的测量点来捕捉到地震信号的主要信息。
假设地震信号 \(x \in \mathbb{R}^N\),它可以在某个基 \(\Psi\) 下表示为:
其中 \(\theta \in \mathbb{R}^N\) 是信号在基 \(\Psi\) 下的系数向量,且 \(\theta\) 是稀疏的,只有少数元素为非零。
通过测量矩阵 \(\Phi \in \mathbb{R}^{M \times N}\)(\(M \ll N\)),我们对信号进行采样,得到观测值:
由于 \(M \ll N\),这是一个欠定方程组。为了恢复稀疏系数向量 \(\theta\),我们可以通过最小化 \(\ell_1\) 范数来求解:
得到 \(\hat{\theta}\) 后,原始信号可以通过 \(x = \Psi \hat{\theta}\) 重建。
压缩感知的核心在于:
- 稀疏性:地震信号在某个基下是稀疏的。
- 测量矩阵的不可压缩性:测量矩阵 \(\Phi\) 与稀疏基 \(\Psi\) 之间的相干性尽可能小,以确保信号的主要信息能够被有效捕捉。
实验(压缩感知在不同实验条件下的重建效果分析)
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import linprog
from sklearn.linear_model import OrthogonalMatchingPursuit
def generate_sparse_signal(N, K):
signal = np.zeros(N)
non_zero_indices = np.random.choice(N, K, replace=False)
signal[non_zero_indices] = np.random.randn(K)
return signal
N = 128
K = 10
sparse_signal = generate_sparse_signal(N, K)
Ms = [50, 80, 100]
bound_conditions = [None, (0, None)]
measurement_matrices = ['Gaussian', 'Bernoulli']
algorithms = ['L1 minimization', 'OMP']
for idx, Ms_part in enumerate([Ms[:2], Ms[2:]]):
plt.figure(figsize=(18, 12), dpi=300)
plot_idx = 1
for M in Ms_part:
for bounds in bound_conditions:
for matrix_type in measurement_matrices:
for algo in algorithms:
if matrix_type == 'Gaussian':
phi = np.random.randn(M, N)
elif matrix_type == 'Bernoulli':
phi = np.random.choice([-1, 1], size=(M, N))
y = phi @ sparse_signal
if algo == 'L1 minimization':
c = np.ones(N)
A_eq = phi
b_eq = y
bounds_l1 = [(0, None) if bounds else (None, None) for _ in range(N)]
result = linprog(c, A_eq=A_eq, b_eq=b_eq, bounds=bounds_l1, method='highs')
if result.success:
reconstructed_signal = result.x
else:
reconstructed_signal = None
elif algo == 'OMP':
omp = OrthogonalMatchingPursuit(n_nonzero_coefs=K)
omp.fit(phi, y)
reconstructed_signal = omp.coef_ if omp.coef_ is not None else None
plt.subplot(len(Ms_part), len(bound_conditions) * len(measurement_matrices) * len(algorithms), plot_idx)
plt.plot(sparse_signal, label='原始稀疏信号', color='blue', linewidth=1.5)
if reconstructed_signal is not None:
plt.plot(reconstructed_signal, label='重建信号', linestyle='--', color='red', linewidth=1.5)
title_text = f'M={M}, {matrix_type}, {algo}, Bound={bounds}'
plt.title(title_text, fontsize=8)
plt.xticks([])
plt.yticks([])
if plot_idx == 1:
plt.legend(fontsize=8, loc='upper right')
plot_idx += 1
plt.suptitle(f'压缩感知不同实验条件下的重建效果对比 - 第 {idx+1} 组', fontsize=20)
plt.subplots_adjust(top=0.88, hspace=0.4)
plt.show()
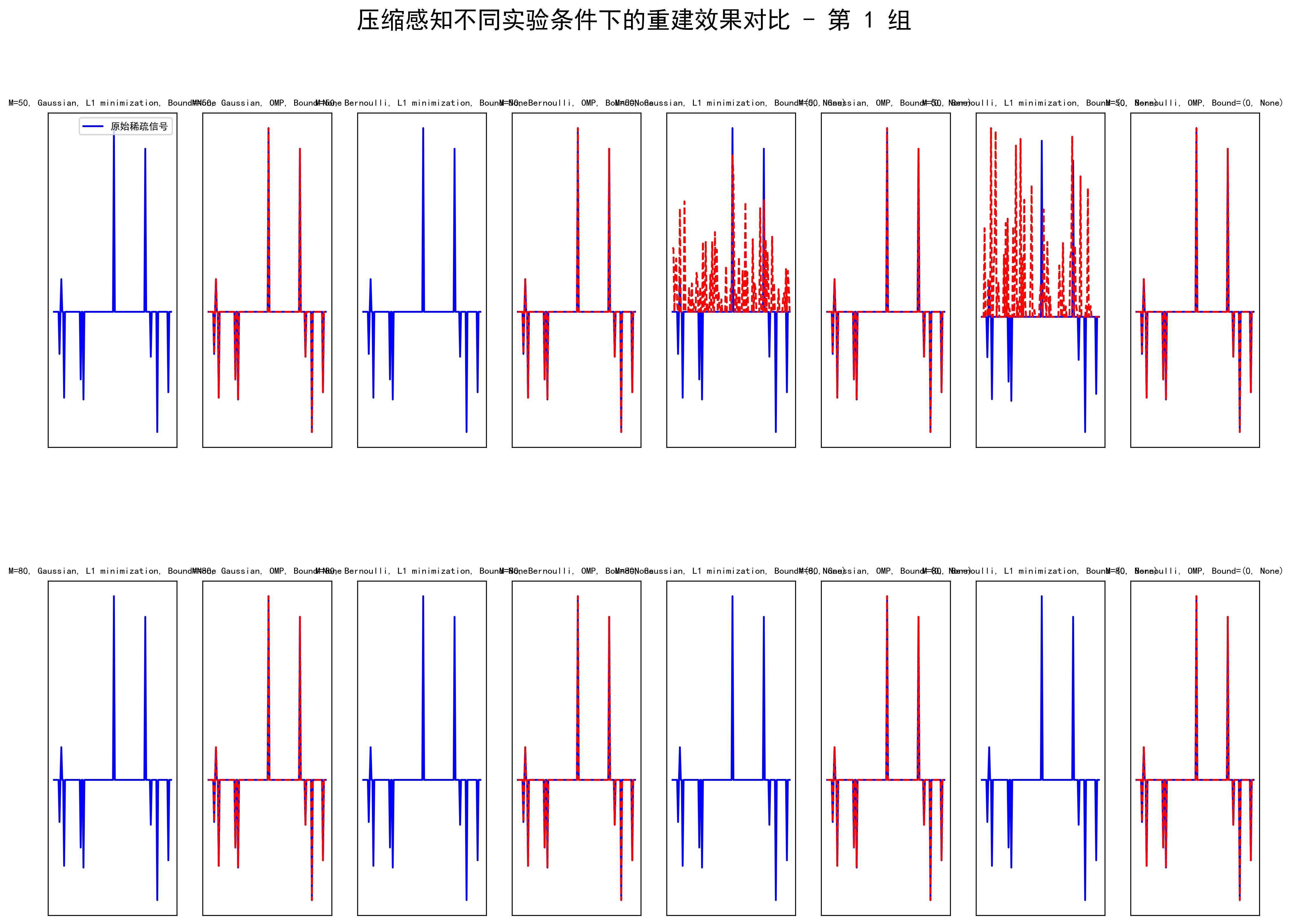
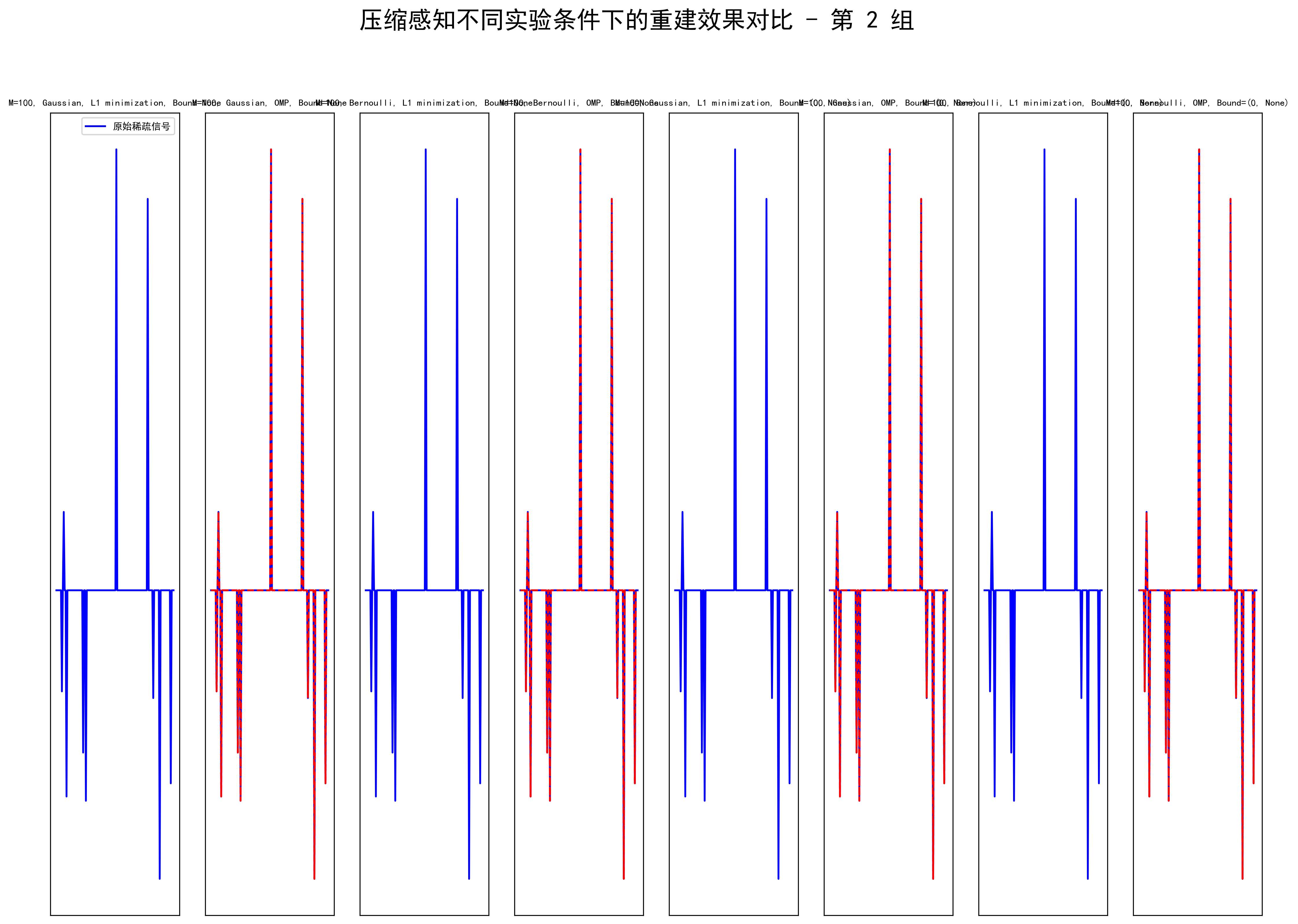
基于这些图像结果,下面对压缩感知在不同实验条件下的重建效果分析。分析分为四个主要部分,涵盖了采样数、测量矩阵类型、重建算法以及边界条件的影响。
从图中可以看出,采样数 $ M $ 对信号的重建效果有明显的影响。当 $ M = 50 $ 时,部分重建信号与原始稀疏信号差异较大,重建效果较差。随着采样数的增加(如 $ M = 80 $ 和 $ M = 100 $),重建信号逐渐趋近于原始信号,特别是在使用 $ L1 $ 最小化和正交匹配追踪(OMP)算法时。这说明采样数越大,观测信息越多,重建质量越好。这是因为更多的观测数据有助于更准确地恢复稀疏信号的非零位置和幅值。
在不同的测量矩阵类型下(高斯矩阵和伯努利矩阵),重建信号的效果存在一定差异。从图中可以观察到,使用高斯矩阵作为测量矩阵时,重建效果往往比伯努利矩阵更稳定,尤其在采样数较少的情况下(如 $ M = 50 $)。这主要是因为高斯矩阵的每列是独立随机的,满足不可压缩性条件更强,能够更好地保留信号的稀疏结构。伯努利矩阵的重建效果则稍差,特别是在低采样率条件下表现出更多噪声。
从不同算法的对比来看, $ L1$ 最小化和正交匹配追踪(OMP)对重建效果有不同的影响。在相同条件下,$ L1$ 最小化通常重建出的信号较为平滑,噪声更少,但可能会导致信号局部幅值被过度平滑。而 OMP 算法在稀疏性要求不太高的情况下(如 $ K = 10$),能更精确地恢复原始稀疏信号的尖锐特征,但对噪声更为敏感。总体而言,OMP 对于非常稀疏的信号表现良好,但 $ L1 $ 最小化在更高稀疏度和低采样条件下更为鲁棒。
实验还测试了是否引入非负边界条件对重建效果的影响。从图中可以看到,当施加非负约束时,部分信号的负幅值被抑制,这对非负信号(如图像数据)可能更有利。然而,在我们的稀疏信号中,这一约束可能并非必要,甚至可能影响重建精度。在某些情况下,添加非负约束会导致信号部分信息丢失,特别是对于包含负值的稀疏信号。因此,边界条件的选取应根据信号的实际特性进行调整。
综合来看,采样数、测量矩阵类型、重建算法和边界条件各自对压缩感知的重建效果有显著影响。总体而言,较高的采样数、使用高斯测量矩阵、采用 $ L1 $ 最小化算法、并根据信号特点适当设置边界条件,是实现良好重建效果的关键。
小结
通过压缩感知技术,我们可以显著减少信号采样的数量,而仍然能够保证信号的精确重建。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号