稀疏信号处理中的惩罚函数与收缩函数

在稀疏信号处理中，惩罚函数和收缩函数是实现信号稀疏性的重要工具，应用于压缩感知、稀疏表示、信号重构等多个方面。通过约束或削弱小幅度系数，保证解的稀疏性。

本文将从惩罚函数和收缩函数的基本概念出发，探讨惩罚函数的选择标准、非凸惩罚函数，以及它们在稀疏信号处理中的应用与理论分析。

---

一、惩罚函数

1.1 惩罚函数的定义和作用

在稀疏信号处理中，惩罚函数是一种附加在目标函数上的正则化项，通过惩罚非零系数来鼓励稀疏解。惩罚函数的选择直接影响解的稀疏性和精确度。

假设我们需要在压缩感知或信号重构中解决以下问题：

\[\min_{x} \frac{1}{2}\|Ax - b\|_2^2 + \lambda P(x) \]

其中，$ A \in \mathbb{R}^{m \times n} $ 是观测矩阵，$ b \in \mathbb{R}^m $ 是观测数据，$ x \in \mathbb{R}^n $ 是待重构的信号，$ P(x) \(为惩罚函数，\)\lambda$ 为正则化参数，用于平衡数据拟合项和稀疏性项。

1.2 常见的惩罚函数及其稀疏性分析

1.2.1 L0 伪范数

L0 伪范数直接度量信号中非零元素的数量：

\[\|x\|_0 = \#\{i : x_i \neq 0\} \]

L0 伪范数严格定义了稀疏性，能精确描述稀疏信号。

在稀疏信号处理中，L0 伪范数是常见的稀疏性度量方式，因为它直接计算信号中非零元素的数量。尽管能准确描述信号的稀疏性，但其非凸性和不可微性导致优化问题非常复杂，因此属于 NP 困难问题，难以直接求解，

为什么会有这些性质，以及它们如何导致 L0 优化问题的求解难度？

注意到！

L0 伪范数的定义为信号中非零元素的个数,在优化中，如果将 L0 伪范数作为目标函数或约束项，即要求解稀疏度最小的解，就会导致一个 非凸优化问题。这是因为 L0 伪范数并不满足凸函数的定义(即在定义域内的任意两点之间，L0 伪范数的值并不总是满足线性插值的条件)。

具体来说的话，L0 伪范数的稀疏度计算是一个分段函数，不会随着信号中每个系数的变化而线性变化。例如，如果 \(x\) 中一个小的非零元素变为零，则稀疏度突然减少，而不再平滑连续地变化。这种不连续的分段特性使得 L0 优化问题的解空间包含多个局部最优解，从而导致一个非凸问题。

而在优化问题中，凸性是优化求解的理想特性，因为对于凸问题，任何局部最优解都是全局最优解，可以通过梯度下降等方法高效地找到最优解。然而，非凸问题则不同，它可能具有多个局部最优解，导致梯度方法无法找到全局最优解。因此，L0 伪范数的非凸性使得求解最稀疏解变得复杂。

L0 伪范数不可微，因为它的值仅依赖于元素是否为零，而不是元素的大小。具体而言，L0 伪范数不对每个分量的连续变化产生连续的响应，且在元素从非零变为零（或反之）时，L0 伪范数会发生突变。这种突变使得在大多数点上不可微。

不可微性进一步增加了优化求解的复杂性，因为经典的优化算法（如梯度下降）依赖于目标函数的导数信息。如果目标函数不可微，则很难通过导数找到函数的最小值，进而无法使用标准的连续优化方法求解 L0 问题。相应的，L0 优化问题通常需要离散的组合优化方法，这些方法在计算上更加复杂且难以实现。

非凸性和不可微性共同导致了 L0 优化问题的 NP 困难性。NP 困难性意味着对于一般的 L0 优化问题，没有已知的多项式时间算法能够在所有情况下求出全局最优解。L0 伪范数的优化问题在数学上属于组合优化问题，求解稀疏度最小的解需要遍历可能的非零元素组合，即在所有变量子集上搜索最优解。

例如，若 \(x\) 含有 \(n\) 个元素，则找到最稀疏的 \(x\) 需要在所有可能的非零子集上进行搜索，组合数为 \(2^n\)，这在计算上呈指数级增长。因此，即使是中等规模的问题，计算时间也会非常长，难以在合理时间内完成。这种计算复杂度导致了 L0 优化问题属于 NP 困难问题，无法通过简单的算法高效求解。

1.2.2 L1 范数

L1 范数是 L0 伪范数的凸近似，定义为：

\[\|x\|_1 = \sum_{i=1}^n |x_i| \]

L1 范数不仅凸且可微分近似，其稀疏解在某些条件下与 L0 伪范数相同。这就是 Lasso 和 Basis Pursuit 等算法的基础，也是稀疏信号处理中最广泛应用的惩罚函数。

下面补充与其相关的内容：

L1 范数是一个凸函数。凸性在数学上定义为，任意两个点之间的连接线上的函数值不大于这两个点上的函数值，即对于任意 \(x, y\) 和 \(t \in [0, 1]\)，满足

\[\|t x + (1 - t) y\|_1 \leq t \|x\|_1 + (1 - t) \|y\|_1 \]

由于绝对值函数本身是凸的，因此 L1 范数也是凸的。这意味着 L1 优化问题可以采用凸优化方法求解，从而保证了算法的稳定性和收敛性。

尽管 L1 范数在零点不可微，但在绝大部分区域内是可微的。与 L0 伪范数相比，L1 范数对小幅度的系数提供了线性惩罚而不是直接舍弃。

这样一来，L1 范数构成了 L0 伪范数的连续可微近似，因此更容易求解，并且在某些条件下（如信号的稀疏性条件），L1 范数优化问题可以得到与 L0 相同的稀疏解。

:::block-1

Lasso 和 Basis Pursuit 的基础

• Lasso 是一种将 L1 范数作为惩罚项的线性回归方法，其目标是最小化以下目标函数：

  \[\min_{x} \frac{1}{2} \|Ax - b\|_2^2 + \lambda \|x\|_1 \]

  其中，\(\lambda\) 控制稀疏性。

  Lasso 通过 L1 惩罚项引入稀疏性，在稀疏信号处理中广泛应用，因为它能自动将某些系数缩小到零，实现特征选择。

• Basis Pursuit 主要应用于稀疏信号重构领域，通过 L1 范数最小化来逼近 L0 优化问题。其目标是找到最小 L1 范数的解，以满足观测方程：

  \[\min_{x} \|x\|_1 \quad \text{s. t. } Ax = b \]

  Basis Pursuit 假设信号在某个稀疏基下可以用少量非零系数表示，并通过 L1 优化找到最稀疏的解。

:::

1.2.3 非凸惩罚函数

• SCAD 是一种非凸惩罚函数，通过一个平滑的非凸曲线来削弱小幅系数的惩罚，减少了 L1 带来的偏差。SCAD 的定义为：

\[ P_{\text{SCAD}}(x; \lambda, a) = \begin{cases} \lambda |x|, & \text{if } |x| \leq \lambda, \\ \frac{-x^2 + 2a\lambda |x| - \lambda^2}{2(a-1)}, & \text{if } \lambda < |x| \leq a\lambda, \\ \frac{\lambda^2(a+1)}{2}, & \text{if } |x| > a\lambda, \end{cases} \]

其中 \(a > 2\) 是一个常数，通常设定为 3.7。

• MCP 是另一种非凸惩罚函数，也能够有效抑制小幅度系数的影响，其定义为：
  \[P_{\text{MCP}}(x; \lambda, \gamma) = \begin{cases} \lambda |x| - \frac{x^2}{2\gamma}, & \text{if } |x| \leq \gamma\lambda, \\ \frac{\gamma \lambda^2}{2}, & \text{if } |x| > \gamma\lambda, \end{cases} \]
  其中 \(\gamma\) 为常数，控制非凸性的强度。

SCAD和 MCP都是稀疏信号处理中常用的非凸惩罚函数。它们的设计目的是克服 L1 范数带来的偏差问题，同时实现信号稀疏化。

SCAD 惩罚函数通过分段定义，依次在不同的区间内对系数进行惩罚调整：

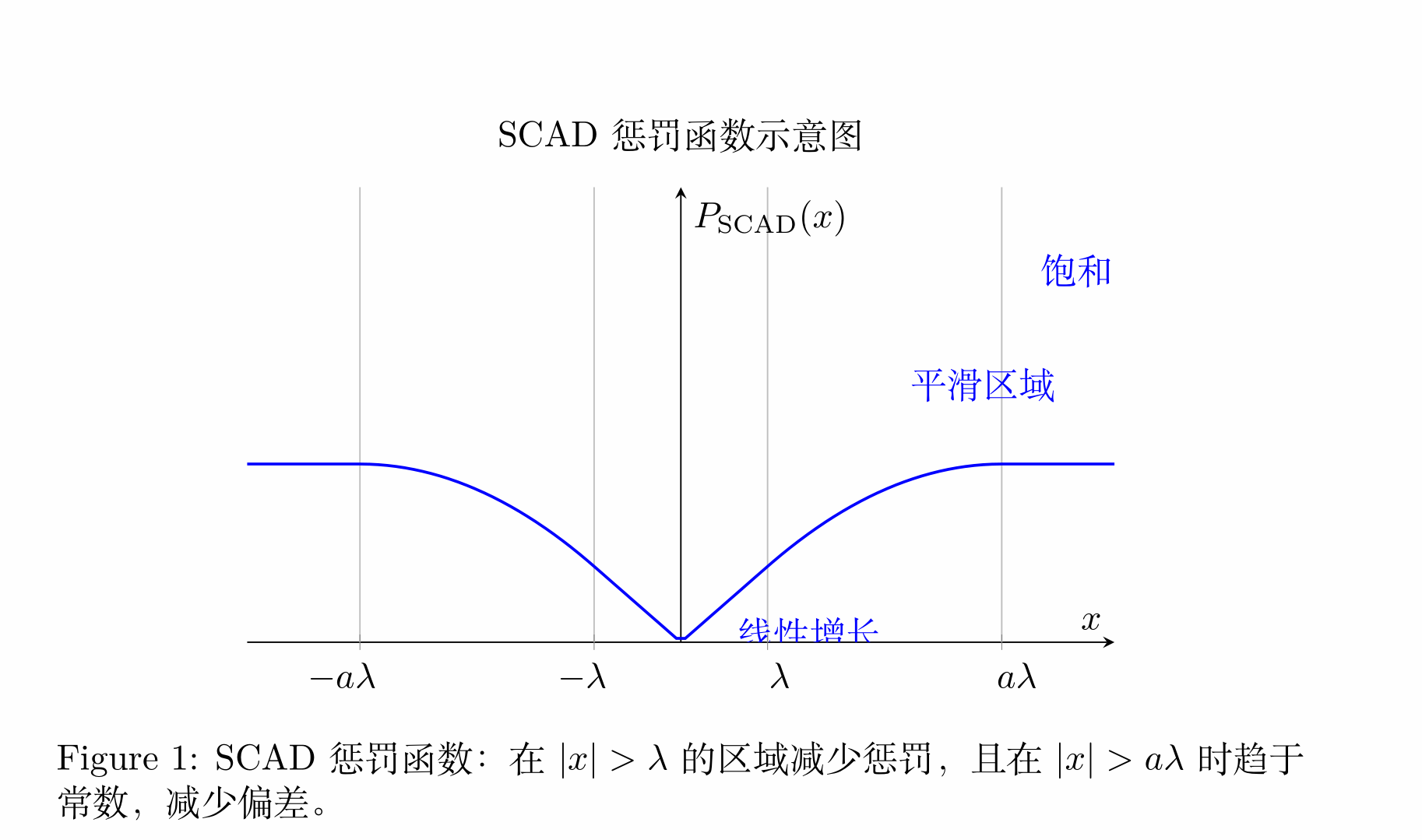
• 当 \(|x| \leq \lambda\) 时，SCAD 惩罚函数的行为类似于 L1 范数，呈现线性增长。这一阶段保持了对小系数的较强惩罚，有助于生成稀疏解。
• 在 \(\lambda < |x| \leq a\lambda\) 区间，惩罚函数逐渐趋于平滑，减少了对较大系数的惩罚。这种设计意图减小 L1 范数带来的偏差问题。
• 当 \(|x| > a\lambda\) 时，SCAD 惩罚函数趋于常数，不再对更大系数增加惩罚，这样能够有效保护信号中的重要信息，避免过度稀疏化。

SCAD 的这种分段非凸形态使得它对小幅度系数有较强的压缩作用，而对大系数惩罚趋于恒定，减少对重要特征的影响。

MCP 惩罚函数的设计也包含分段结构，但其形式更为简洁：

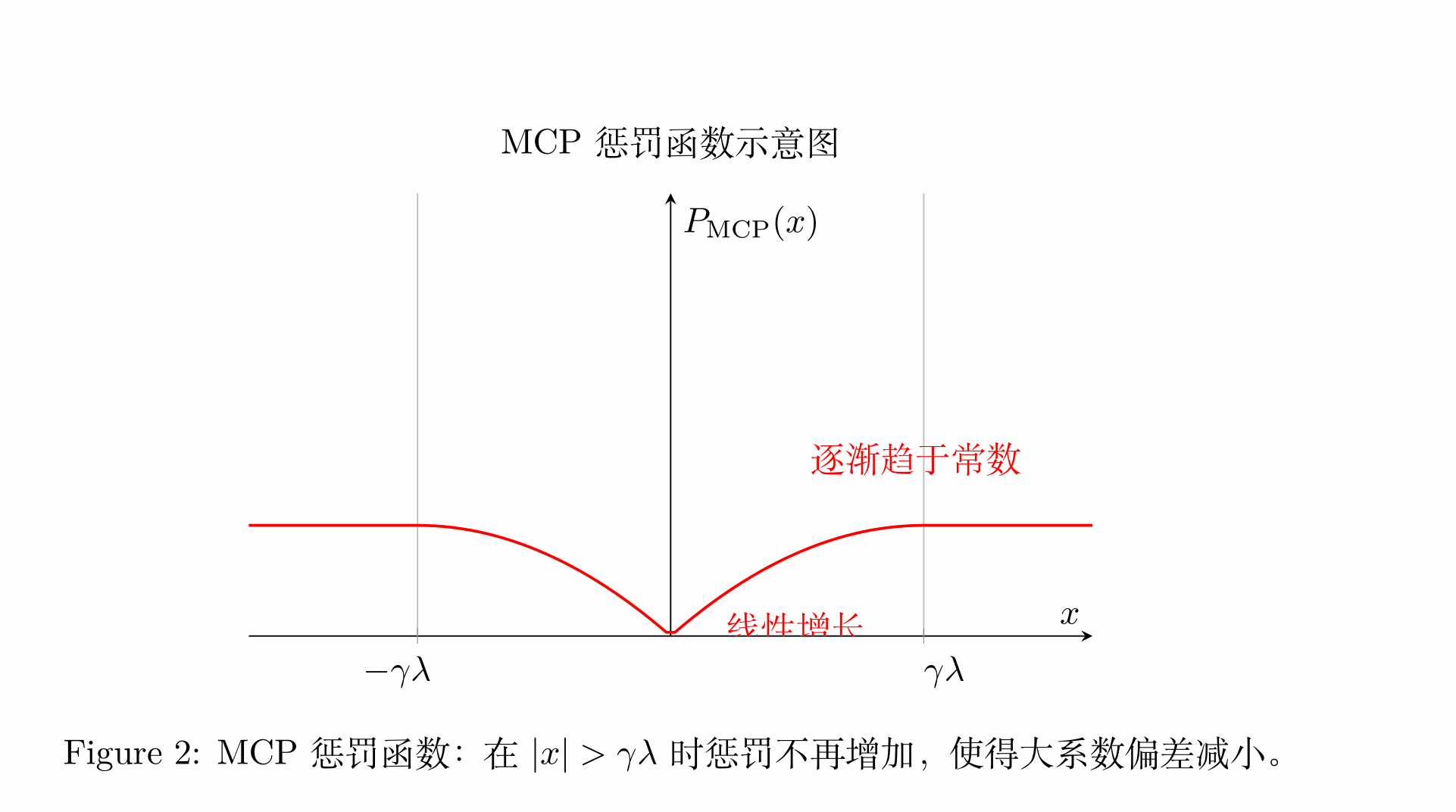
• 当 \(|x| \leq \gamma \lambda\) 时，MCP 惩罚函数类似 L1 范数，呈现线性增长，不过增长速度逐渐减缓。
• 在 \(|x| > \gamma \lambda\) 区间内，MCP 函数的惩罚值保持不变，达到一个固定常数，不再对大系数进行额外惩罚。

与 SCAD 相比，MCP 的过渡区间较短，非凸性控制更为简单，因而在一定程度上减少了对大系数的偏差，但对小系数的压缩效果可能略弱于 SCAD。

我们再从偏差控制与稀疏性进行分析：

SCAD 惩罚函数的设计目的之一是减少 L1 惩罚带来的偏差。L1 惩罚对所有非零系数施加等量的线性惩罚，导致大系数也会受到同样的缩减，从而影响信号的重构精度。SCAD 通过在 \(\lambda < |x| \leq a\lambda\) 区间逐渐减小惩罚强度，从而对大系数进行保护，避免对重要特征的压缩。这使得 SCAD 在生成稀疏解的同时，能够更准确地保留信号的幅度。

MCP 的设计目标是同样减少 L1 带来的偏差。不同于 SCAD，MCP 的非凸性在 \(|x| > \gamma \lambda\) 时直接达到常数，不再对大系数施加惩罚。这一设计使得 MCP 能在稀疏性和偏差控制之间达到良好的平衡，特别适合在特征数量较多但信号稀疏性较弱的情况下使用。

在稀疏性方面，SCAD 和 MCP 均可有效生成稀疏解，但由于 SCAD 的惩罚在小系数区域更强，因此在高稀疏性要求的场景下，SCAD 的表现可能优于 MCP.

:::block-1
另外，SCAD 的非凸性和分段定义导致其优化问题复杂度较高。SCAD 优化往往需要迭代算法，并且可能会产生多个局部最优解，增加了求解难度。常用的优化方法包括近似算法和启发式算法，如坐标下降法、ADMM等，来寻找合适的解。

与 SCAD 相比，MCP 的定义更为简洁，因此在优化过程中可能更加高效。MCP 由于其较短的平滑区间，优化难度相对较低，迭代收敛速度较快。对于 MCP 的优化，坐标下降法和迭代收缩阈值算法（ISTA）是常用的方法，能有效在稀疏解和低计算复杂度之间取得平衡。
:::

比较维度	SCAD	MCP
惩罚机制	分段式，线性增长、平滑、饱和	分段式，线性增长，逐渐趋于常数
偏差控制	对大系数惩罚减少，保留重要特征	直接达到常数，偏差控制简单
稀疏性效果	高稀疏性需求下表现良好	稀疏性稍弱，但计算更高效
优化难度	优化复杂，多个局部最优	相对简洁，优化较快

1.2.4 惩罚函数的选择标准

惩罚函数的选择主要取决于以下几个因素：

1. 稀疏性要求：L0 和 L1 范数更倾向于生成稀疏解，而 SCAD 和 MCP 在产生稀疏性时偏差较小。
2. 计算复杂度：L1 范数因其凸性较易求解，而非凸惩罚（如 SCAD、MCP）难以求解，通常需要特殊的优化算法。
3. 解的稳定性：L1 范数可能导致偏差，特别是在稀疏度较高时，而 SCAD 和 MCP 能在一定程度上减少偏差，得到更准确的解。

---

二、收缩函数

2.1 收缩函数的定义

收缩函数是对解进行逐项收缩的操作，削弱小幅度系数的影响。它通常用于解决含有 L1 惩罚项的优化问题。

2.2 常见的收缩函数及其作用

2.2.1 软阈值收缩

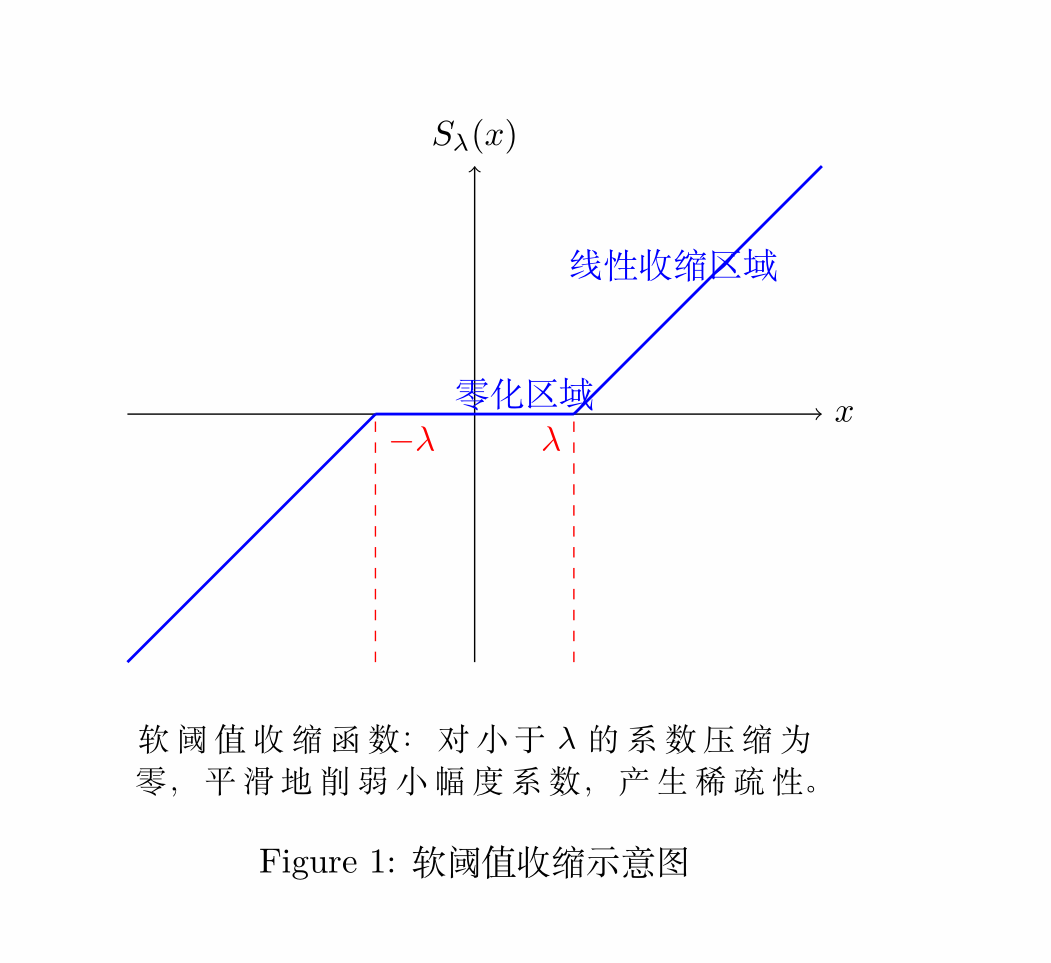
在 L1 范数惩罚下，问题的最优解可以通过软阈值收缩来得到。软阈值收缩函数定义为：

\[S_{\lambda}(x) = \text{sgn}(x) \cdot \max(|x| - \lambda, 0) \]

软阈值收缩对小于阈值的系数设为零，削弱了小幅度系数的影响，保持了稀疏性。

2.2.2 硬阈值收缩

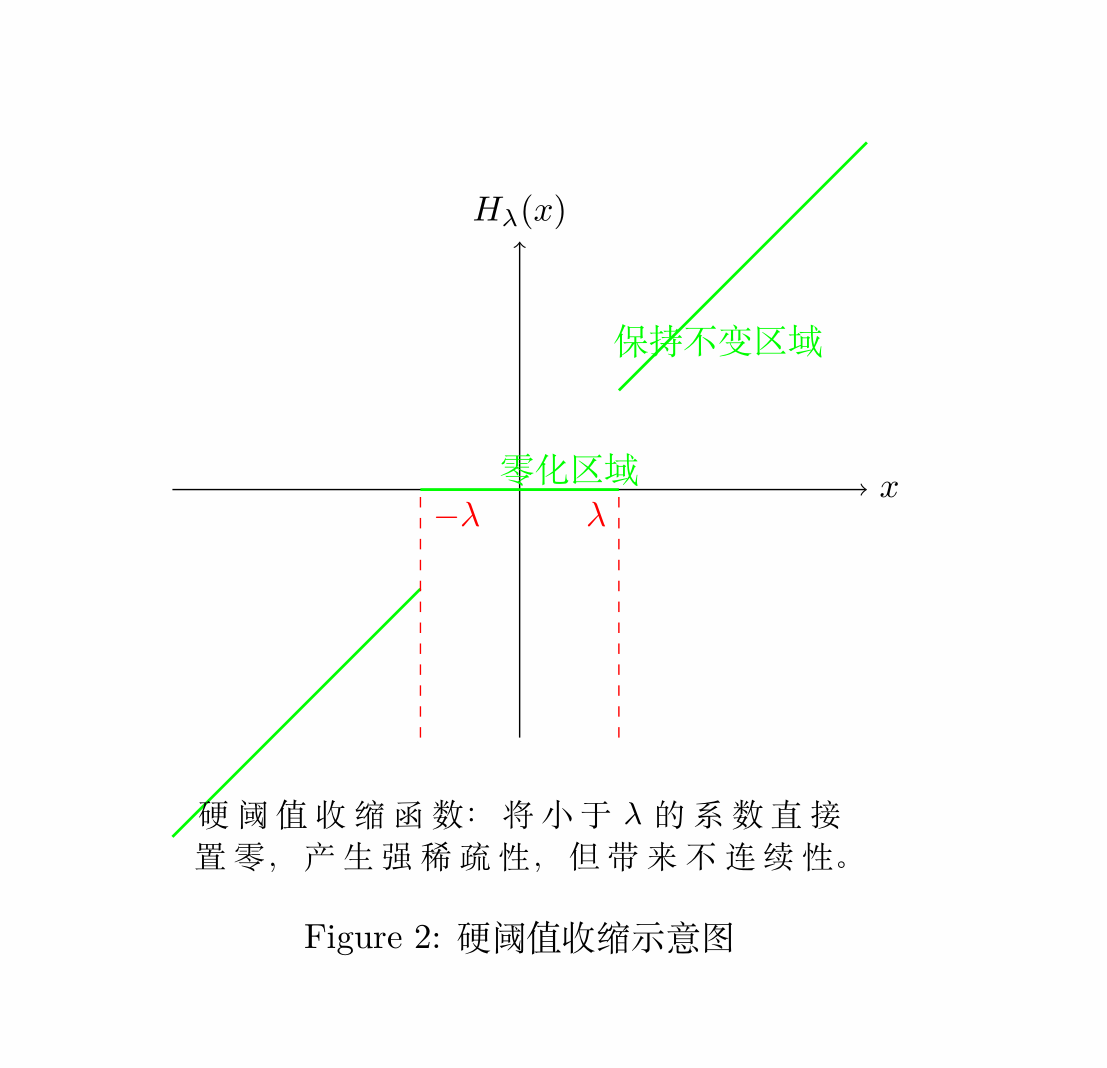
硬阈值收缩函数直接将小于阈值的系数置零，高于阈值的系数保持不变：

\[H_{\lambda}(x) = \begin{cases} x, & \text{if } |x| > \lambda, \\ 0, & \text{if } |x| \leq \lambda. \end{cases} \]

硬阈值收缩更直接产生稀疏性，但可能带来不连续性，导致求解不稳定。

---

三、小结

惩罚函数和收缩函数是稀疏信号处理中的关键工具，影响着解的稀疏性和稳定性。