压缩感知

压缩感知

压缩感知是一种突破传统采样定理的信号处理技术。为了理解压缩感知的革新性，我们首先回顾奈奎斯特-香农采样定理。

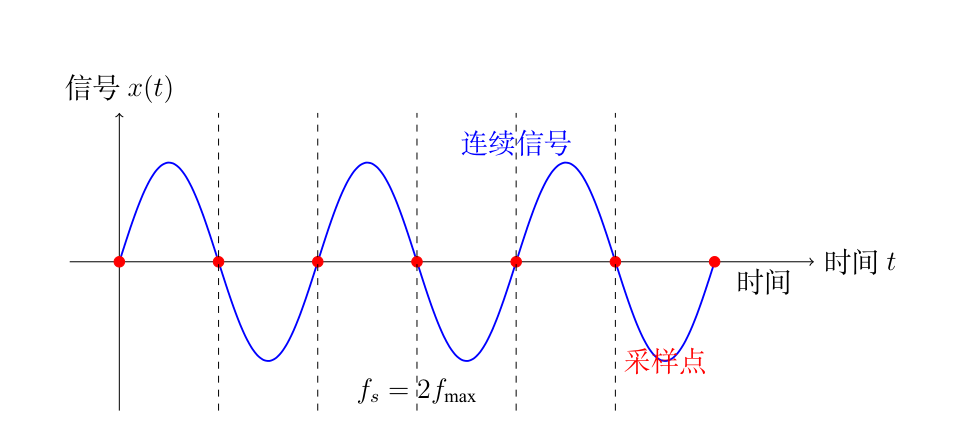
• 奈奎斯特-香农采样定理

奈奎斯特-香农采样定理是信号处理中的一个基础理论，描述了如何从离散的采样点精确地重建连续信号。它指出：

一个带限信号，即其频谱中最高频率为 $ f_{\text{max}} $ 的信号，必须以至少两倍于其最高频率的速率进行采样，才能保证采样后的信号可以无失真地重建。

• 采样定理公式

采样频率 $ f_s $ 必须满足：

\[f_s \geq 2 f_{\text{max}} \]

其中，$ f_s $ 是采样频率，$ f_{\text{max}} $ 是信号中的最高频率。

• 混叠现象

当采样频率低于奈奎斯特频率时，信号的高频分量在采样过程中会折叠回低频区间，导致混叠现象。混叠现象使得原始信号的高频成分无法从采样点中正确恢复，导致失真。

• 采样与重建

奈奎斯特-香农采样定理说明了，如果信号带宽有限且采样速率大于等于信号的奈奎斯特频率（即两倍的信号最高频率），则可以通过插值公式无失真地从采样点重建原始信号。

采样信号 $ x(nT) $（其中 $ T = \frac{1}{f_s}$ 是采样间隔）可以通过以下公式恢复连续信号 $ x(t) $：

\[x(t) = \sum_{n=-\infty}^{\infty} x(nT) \, \text{sinc} \left( \frac{t - nT}{T} \right) \]

其中，\(\text{sinc}(t) = \frac{\sin(\pi t)}{\pi t}\) 是一个核函数，用于在时间域中进行插值。

• 奈奎斯特-香农定理的局限

尽管奈奎斯特-香农定理为带限信号的精确采样提供了理论保障，但在许多实际应用中存在局限性：

1.随着传感器和信号采集设备的普及，过高的采样速率导致了大规模的数据存储和处理挑战。例如，在医学成像中，过高的采样速率会导致数据量过大，增加处理和存储成本。

2.许多自然信号（如图像、音频等）在某些变换域（例如傅里叶域、小波域）中是稀疏的，大部分系数接近于零。采样所有信号点显得不必要，因为绝大多数信息可以通过少量重要系数表达。

3.随着信号维度的增加，传统采样方法所需的数据量迅速增长。这在处理高维数据（如高分辨率图像、视频等）时尤为突出。

• 压缩感知

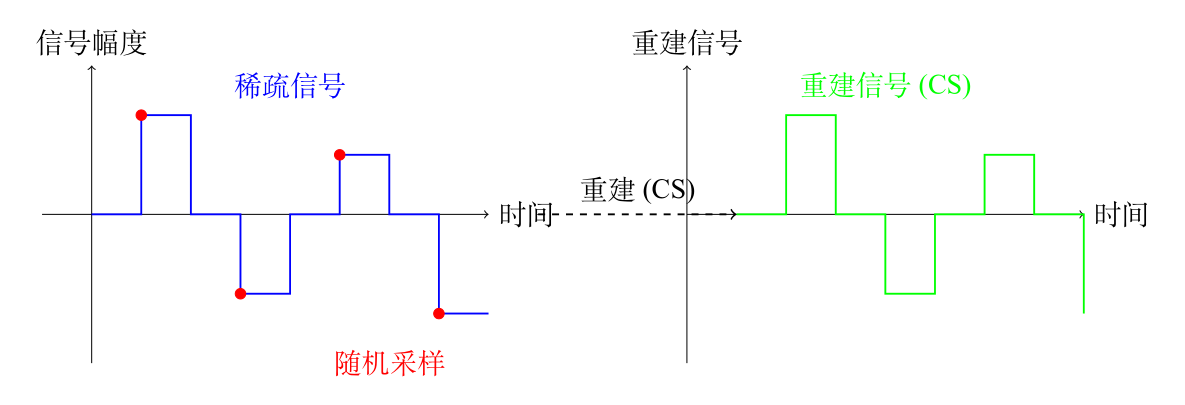
压缩感知（CS） 利用信号的稀疏性，实现了远低于奈奎斯特频率的采样速率，并能够精确重建信号。它突破了奈奎斯特频率的限制，基于信号在特定变换域中的稀疏性进行采样。

• 基本思想

压缩感知的核心思想是：如果信号在某个变换域中是稀疏的，则可以使用远少于信号本身维度的采样点来重建信号。

假设一个信号 $ x \in \mathbb{R}^N $，而它在某个基下具有稀疏表示：

\[x = \Psi \theta \]

其中：

• $ x $ 是原始信号，维度为 $ N $；
• $ \Psi $ 是稀疏基或字典；
• $ \theta $ 是信号在该基下的系数向量，其中只有少数元素非零。

然后通过线性测量矩阵 $ \Phi $ 采集 $ M \ll N $ 个观测值：

\[y = \Phi x = \Phi \Psi \theta \]

其中 \(y\) 是压缩感知的观测结果。

通过求解这个欠定方程，我们可以恢复信号 \(x\)。

• 测量矩阵与不可压缩性

在压缩感知中，测量矩阵 $ \Phi $ 应该满足不可压缩性（incoherence），即测量矩阵和稀疏基 $ \Psi $ 之间的关联性要尽可能低。例如，随机高斯矩阵和伯努利矩阵常用于压缩感知中作为测量矩阵，因为它们具有很好的不可压缩性。

• 信号重建过程

信号的重建是通过最小化 $ \ell_1 $ 范数来完成的，即通过以下凸优化问题重建稀疏信号：

\[\hat{\theta} = \arg \min \|\theta\|_1 \quad \text{s. t.} \quad y = \Phi \Psi \theta \]

一旦得到 $ \hat{\theta}$，信号 $ x $ 可以通过：

\[x = \Psi \hat{\theta} \]

进行重建。

• 重建算法

压缩感知的信号重建问题本质上是一个凸优化问题。常用的重建算法包括：

基追踪：通过最小化 $ \ell_1 $ 范数实现稀疏信号的重建。

正交匹配追踪（OMP）：一种迭代算法，通过逐步选择与观测值最相关的基向量来重建信号。

这些算法的设计初衷是为了高效地求解欠定方程，恢复原始信号的稀疏系数。

• 小结

通过压缩感知，信号采样数量可以显著减少，而信号的重建精度仍然可以得到保证。压缩感知理论突破了传统奈奎斯特-香农采样定理的限制，尤其在处理稀疏信号和高维数据时具有广泛的应用。它的成功得益于信号的稀疏性和测量矩阵的不可压缩性，以及求解凸优化问题的先进算法。

---

补充说明

稀疏性是指信号在某个基下可以用少量的非零系数来表示，即大多数系数为零或接近零。稀疏性是压缩感知的核心基础之一，它保证了我们能够以较少的观测数据来重建原始信号。

• 稀疏性的定义:

假设信号 $ x \in \mathbb{R}^N $，它可以在某个基 $ \Psi$ 下表示为：

\[x = \Psi \theta \]

其中 $ \theta \in \mathbb{R}^N $ 是信号在基 $ \Psi $ 下的系数向量。如果 $ \theta $ 中的非零元素个数为$ k$，即信号在该基下是k-稀疏的，那么：

\[\|\theta\|_0 = k \quad \text{其中} \quad k \ll N \]

这里 $ |\theta|_0 $ 表示向量 $ \theta $ 的零范数，即非零元素的个数。

• 稀疏信号的重建

在压缩感知中，我们通过测量矩阵 $ \Phi $ 进行少量采样：

\[y = \Phi x = \Phi \Psi \theta \]

其中，观测值 $ y \in \mathbb{R}^M $ 是原信号经过测量矩阵$\Phi $ 后得到的，且 $ M \ll N $。

由于信号 $ x $ 在基 $ \Psi $ 下是稀疏的，即 $ k $-稀疏，重建问题可以被归结为在给定的观测值 $ y $ 和测量矩阵 $ \Phi$ 的条件下，求解稀疏系数 $ \theta$ 的优化问题：

\[\hat{\theta} = \arg \min \|\theta\|_0 \quad \text{subject to} \quad y = \Phi \Psi \theta \]

这个优化问题由于零范数的离散性是 NP-hard 的，因此实际中我们通过最小化 $ \ell_1 $ 范数作为稀疏解的近似：

\[\hat{\theta} = \arg \min \|\theta\|_1 \quad \text{subject to} \quad y = \Phi \Psi \theta \]

这里使用 $ \ell_1 $-范数的原因是，虽然 $ \ell_0 $-范数直接表达了稀疏性，但它是非凸的，难以优化。而 $ \ell_1 $-范数是凸的，并且在一定条件下，最小化 $ \ell_1 $-范数能够给出与 $\ell_0 $-范数相同的稀疏解。

• 2. 不可压缩性（Incoherence）的证明

压缩感知的另一个重要性质是不可压缩性，即测量矩阵 $ \Phi $ 和稀疏基 $ \Psi $ 之间的相关性尽可能低。不可压缩性保证了从少量的随机采样中可以有效恢复信号的稀疏系数。

• 不可压缩性的定义

假设信号$ x = \Psi \theta $ 是在基 $ \Psi $ 下的稀疏表示，而我们通过测量矩阵 $ \Phi $ 采集观测值$ y = \Phi x \(。若测量矩阵\) \Phi $ 和稀疏基 $ \Psi$ 满足不可压缩性条件，则它们之间的内积尽可能小。这可以通过内积的最大值来衡量：

\[\mu(\Phi, \Psi) = \max_{i,j} |\langle \phi_i, \psi_j \rangle| \]

其中 $ \phi_i $ 是测量矩阵 $ \Phi $ 的第 $ i $ 列，$ \psi_j $ 是稀疏基$ \Psi$ 的第 $ j $ 列。

不可压缩性要求内积 $ \mu(\Phi, \Psi) $ 尽可能小，即测量矩阵和稀疏基之间是弱相关的。典型的测量矩阵如随机高斯矩阵和随机伯努利矩阵具有很好的不可压缩性。

:::block-1

• 不可压缩性的证明思路

1. 相干性和信号重建能力：

   注意到，相干性描述了两个基（或者矩阵）之间的最大相关性。若测量矩阵 $ \Phi $ 和稀疏基 $ \Psi $高度相关，那么信号的投影将集中在某几个特定方向上，从而无法有效地分离出信号的稀疏成分。而当 $ \Phi $ 和$ \Psi $ 不相关时，信号的信息能够更加均匀地分布在测量矩阵的列中，使得即便使用少量的随机测量点，也能较好地捕捉信号的全部信息。

   在测量矩阵与稀疏基相互不相关的情况下，信号重建问题的欠定性可以得到缓解，从而通过最小化 $ \ell_1$ 范数来精确重建信号。

2. 测量矩阵的设计：

   理论上，若测量矩阵$\Phi $ 是随机矩阵（如高斯随机矩阵或伯努利随机矩阵），则可以证明它与几乎所有的基 $ \Psi $ 之间都是不可压缩的。这一性质是基于高维几何中的随机投影理论，即随机矩阵的列向量与基向量的内积在概率上具有良好的分布特性。

   实际上，对于随机矩阵 $ \Phi $，通过集中不等式可以证明其与任意固定基 $ \Psi $ 之间的内积在较高的概率下是接近于零的。这使得即使使用少量测量，也能较好地重建信号。

• 测量矩阵与稀疏基的不可压缩性保证了压缩感知重建的精度：

若测量矩阵和稀疏基之间的相干性较小，则可以确保通过最小化 $\ell_1 $ 范数来恢复原始信号。同时，若测量矩阵是高斯随机矩阵或者伯努利矩阵，其不可压缩性能够在理论上保证重建信号的精度。
:::