BP

稀疏信号重建 | 基追踪

基追踪算法（BP）是一种用于稀疏信号重建的优化方法，在压缩感知（ CS）和稀疏表示领域中具有重要作用。它通过 $ l_1 $ 正则化解决稀疏重建问题，能够在信号稀疏度未知的情况下获得较高的重建精度。本文讲解该算法的提出动机、原理，以及背后的理论相关过程。

---

1. 基追踪算法的提出动机

在许多应用中，例如图像处理、信号处理和数据压缩，我们经常会遇到一些稀疏的信号，即信号可以用少量非零分量来精确或近似表示。但是，由于观测数据不完整或受限，我们无法直接观测到完整信号。为了重建这种稀疏信号，传统的 $ l_0 $ 正则化方案理论上是理想的选择。

然而，$ l_0 $ 正则化问题的求解是一个 NP 难问题，因为它需要在所有可能的分量组合中找到最优解，这在计算上不可行。

在稀疏信号重建中，我们期望找到一个信号的最稀疏表示，即一个最小化非零元素数量的表示。数学上，这个问题可以用 $ l_0 $ 正则化表达：

\[\min \|x\|_0 \quad \text{s.t.} \quad y = \Phi x \]

其中，$ |x|_0 $ 表示向量 $ x $ 中非零元素的个数，$ y $ 是测量值，$ \Phi $ 是测量矩阵。该问题的目标是找到一个满足 $ y = \Phi x $ 的稀疏向量 $ x $，即在满足方程的情况下，使得非零元素的数量最少。

这种问题被称为 NP 难问题，是因为：

求解 $ l_0 $ 正则化问题本质上是一个组合优化问题，要求找到使得非零分量最少的组合。设 $ x $ 的长度为 $ n $，目标是从 $ n $ 个可能的位置中选取最少的非零分量组合，这样的问题属于组合优化问题，其复杂度随着 $ n $ 的增长呈指数增长。

要找到最稀疏的解，需要检查所有可能的组合。假设我们不知道稀疏度 $ k $，那么对于一个 $ n $-维向量 $ x $，理论上需要遍历所有的 $ 2^n $ 种情况，以找到使得 $ y = \Phi x $ 成立的最稀疏解。这种遍历操作的复杂度为 $ O(2^n) $，属于指数时间复杂度。而对于一个 NP 问题来说，其求解时间复杂度会随着输入规模呈指数增长，这就是该问题被归为 NP 难的原因。

对于大规模数据或高维信号，计算所有可能组合以确定最稀疏解是不可行的。这意味着在实际应用中，使用 $ l_0 $ 正则化进行稀疏重建会导致不可接受的计算时间。

进一步解释 NP 难性,即非确定性多项式时间难题，指的是没有已知的算法能够在多项式时间内求解此类问题。更正式的定义是：如果一个问题的解可以在多项式时间内验证，但不能在多项式时间内求解，则称之为 NP 完全问题。如果一个问题至少和 NP 完全问题一样难求解，则称其为 NP 难。

在 $ l_0 $ 正则化中，我们面临的情况是，给定一个 $ y $ 和测量矩阵 $ \Phi $，找到最小的稀疏向量 $x $ 使得 $ y = \Phi x $。这需要在大量的可能解中找到最优解。验证一个解是否符合稀疏度要求较为简单（即验证该解是否满足方程且稀疏性最优），但要找到最优解却难以实现，因为它涉及到所有组合情况的遍历。

由于 $ l_0 $ 正则化问题属于 NP 难问题，基追踪算法使用了 $ l_1 $ 正则化作为替代。$ l_1 $ 正则化的目标是最小化 $ x $ 的 $ l_1 $ 范数：

\[\min \|x\|_1 \quad \text{s.t.} \quad y = \Phi x \]

这里的 $ l_1 $ 范数 \(\|x\|_1 = \sum_{i=1}^n |x_i|\) 是一个凸函数，因此 $ l_1 $ 正则化问题是一个凸优化问题。凸优化问题可以在多项式时间内求解，这大大降低了计算复杂度，因此在实际应用中更加可行。理论上也可以证明，当测量矩阵满足一定条件（如 RIP 条件）时，$ l_1 $ 正则化的解可以接近甚至等同于 $ l_0 $ 正则化的解，从而达到有效的稀疏信号重建。

---

2. 基追踪算法的原理

假设我们有一个测量矩阵 $ \Phi \in \mathbb{R}^{m \times n} $ 和观测向量 $ y \in \mathbb{R}^m $，其中 $ m \ll n $，因此我们面临一个欠定方程组：

\[y = \Phi x \]

我们希望找到一个稀疏解 $ x $ 使得该方程成立。稀疏解可以通过以下 $ l_0 $ 优化问题来定义：

\[\min \|x\|_0 \quad \text{s.t.} \quad y = \Phi x \]

但 $ l_0 $ 正则化问题求解困难，因此我们将问题转换为一个 $ l_1 $正则化问题：

\[\min \|x\|_1 \quad \text{s.t.} \quad y = \Phi x \]

其中，\(\|x\|_1 = \sum_{i=1}^n |x_i|\) 表示 $ x $ 的 $ l_1 $ 范数。

为什么用 $ l_1 $ 替代 $l_0 $ ?

$ l_1 $ 范数是一个凸函数，而 $ l_0 $ 范数不是凸的。因此，$ l_1 $ 优化可以通过凸优化技术高效求解。

压缩感知理论表明，当满足一定条件（如 RIP 条件或测量矩阵的稀疏性）时，$l_1 $ 优化解即为 $ l_0 $ 优化解。

在一定的稀疏条件下，$ l_1 $ 优化的解不仅稀疏，而且是唯一的，因此这种方法能够有效地得到稀疏解。

另外，基追踪算法之所以能够有效地进行稀疏重建，依赖于一些关键理论，包括稀疏性、测量矩阵的结构以及最优性条件。

• 稀疏性和唯一解

假设向量 $ x $ 是 $ k $-稀疏的，即仅有 $ k $ 个非零分量。当测量矩阵 $ \Phi $ 满足特定条件时，基追踪算法的 $ l_1 $ 最小化问题可以得到稀疏的唯一解。这一结果可以通过以下理论来解释：

如果测量矩阵 $ \Phi $ 满足特定的稀疏正则化条件（如 RIP 条件），则可以证明 $ l_1 $ 正则化问题的解即为最稀疏的唯一解。

对于一个 $ k $-稀疏信号，当测量矩阵 $ \Phi $ 满足 RIP 条件且 $ m \geq C \cdot k \log(n/k) $ 时（其中 $ C $ 为常数），可以通过 $ l_1 $ 优化精确重建信号。

• RIP 条件与基追踪的重建精度

限制等距性质（RIP）是评估测量矩阵是否适合稀疏信号重建的一个重要条件。一个矩阵 $ \Phi $ 被称为满足 $ k $-阶 RIP 条件，如果对于任意 $ k $-稀疏向量 $ x $，存在常数 $ \delta_k \in (0,1) $ 使得：

\[(1 - \delta_k) \|x\|_2^2 \leq \|\Phi x\|_2^2 \leq (1 + \delta_k) \|x\|_2^2 \]

该条件确保了不同稀疏向量经过矩阵变换后能够保持足够的距离差异，从而避免信息丢失,基追踪算法在满足 RIP 条件时，可以有效地进行稀疏信号重建。

---

3. 基追踪算法的求解方法

基追踪算法可以通过凸优化算法求解。常见的求解方法包括：线性规划、迭代收缩阈值算法、快速迭代收缩阈值算法.

下面是使用Python实现基追踪算法的三种求解方法示例，首先生成随机稀疏信号和测量矩阵，再利用三种方法重建信号，并对比结果。

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import linprog
from numpy.linalg import norm
from matplotlib import rcParams

rcParams['font.sans-serif'] = ['SimHei']
rcParams['axes.unicode_minus'] = False
rcParams['figure.dpi'] = 300

np.random.seed(42)
n, m, k = 100, 50, 10  
x_true = np.zeros(n)
x_true[np.random.choice(n, k, replace=False)] = np.random.randn(k) * 10 
phi = np.random.randn(m, n) 
y = phi @ x_true 

# 定义L1范数最小化线性规划求解
def linear_programming(phi, y):
    c = np.ones(n)
    A_eq = np.vstack([phi, -phi])
    b_eq = np.hstack([y, -y])
    result = linprog(c, A_eq=A_eq, b_eq=b_eq, bounds=(None, None), method='highs')
    return result.x if result.success else np.zeros(n)

# 定义ISTA算法求解
def ista(phi, y, alpha=0.001, max_iter=500):
    x = np.zeros(n)
    for _ in range(max_iter):
        grad = phi.T @ (phi @ x - y)
        x = np.sign(x - alpha * grad) * np.maximum(np.abs(x - alpha * grad) - alpha, 0)
    return x

# 定义FISTA算法求解
def fista(phi, y, alpha=0.001, max_iter=500):
    x = np.zeros(n)
    t = 1
    z = x.copy()
    for _ in range(max_iter):
        x_old = x.copy()
        grad = phi.T @ (phi @ z - y)
        x = np.sign(z - alpha * grad) * np.maximum(np.abs(z - alpha * grad) - alpha, 0)
        t_new = (1 + np.sqrt(1 + 4 * t ** 2)) / 2
        z = x + ((t - 1) / t_new) * (x - x_old)
        t = t_new
    return x

x_lp = linear_programming(phi, y)
x_ista = ista(phi, y)
x_fista = fista(phi, y)

plt.figure(figsize=(15, 10))
plt.subplot(3, 1, 1)
plt.plot(x_true, label="真实稀疏信号", color="navy", linewidth=2)
plt.plot(x_lp, linestyle="--", color="darkred", label="线性规划重建", linewidth=2)
plt.xlabel("信号索引", fontsize=14)
plt.ylabel("幅值", fontsize=14)
plt.title("线性规划重建效果", fontsize=16)
plt.legend(loc="upper right", fontsize=12, frameon=False)
plt.grid(True, linestyle='--', alpha=0.6)
plt.subplot(3, 1, 2)
plt.plot(x_true, label="真实稀疏信号", color="navy", linewidth=2)
plt.plot(x_ista, linestyle="-.", color="darkgreen", label="ISTA重建", linewidth=2)
plt.xlabel("信号索引", fontsize=14)
plt.ylabel("幅值", fontsize=14)
plt.title("ISTA 重建效果", fontsize=16)
plt.legend(loc="upper right", fontsize=12, frameon=False)
plt.grid(True, linestyle='--', alpha=0.6)
plt.subplot(3, 1, 3)
plt.plot(x_true, label="真实稀疏信号", color="navy", linewidth=2)
plt.plot(x_fista, linestyle=":", color="purple", label="FISTA重建", linewidth=2)
plt.xlabel("信号索引", fontsize=14)
plt.ylabel("幅值", fontsize=14)
plt.title("FISTA 重建效果", fontsize=16)
plt.legend(loc="upper right", fontsize=12, frameon=False)
plt.grid(True, linestyle='--', alpha=0.6)

plt.tight_layout()
plt.show()

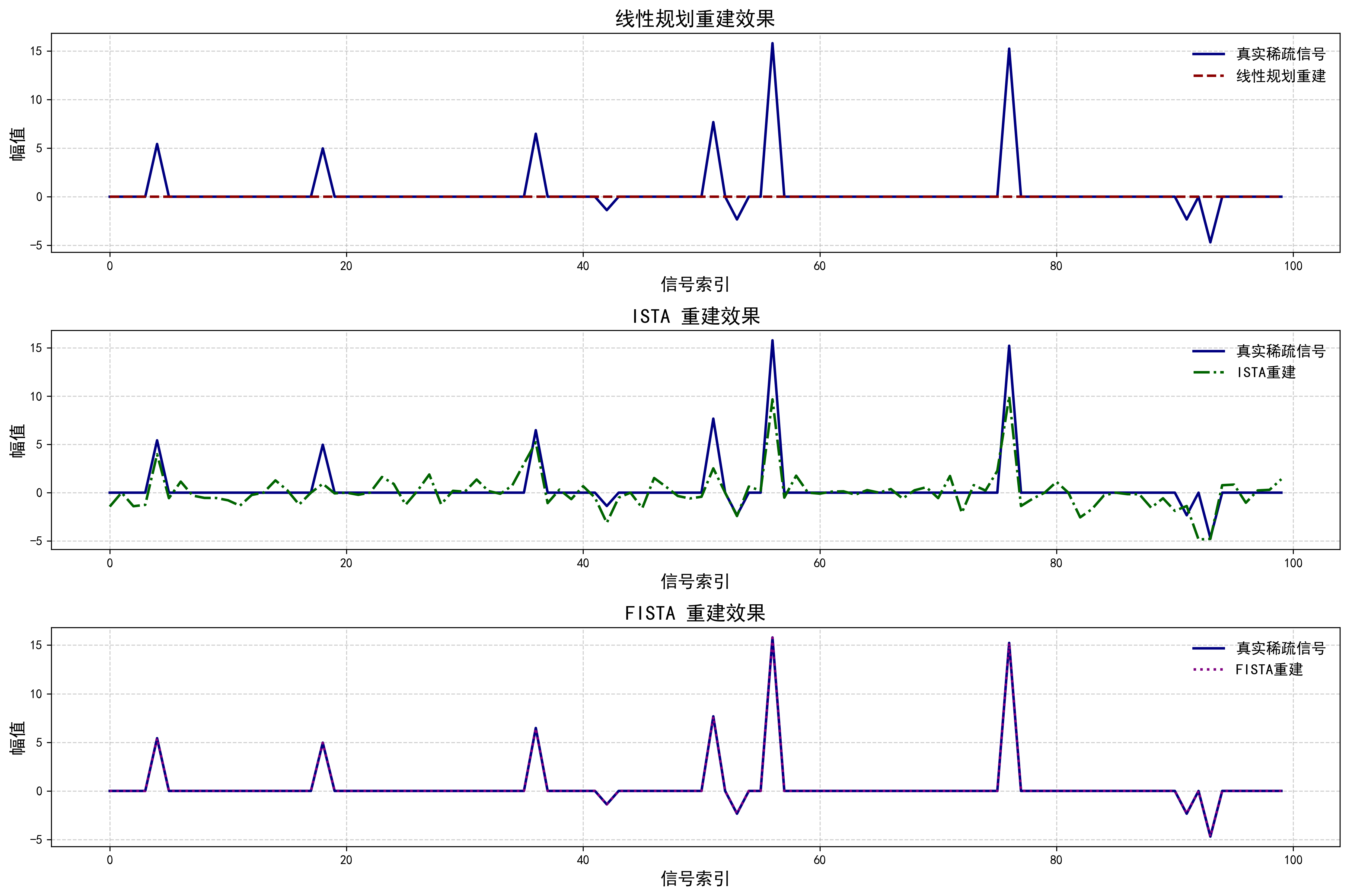
根据图1，我们得到以下两点

第一，线性规划方法在重建稀疏信号方面能够较好地找到信号的非零位置，但其重建结果的峰值较低，基本呈现为一条接近于零的直线。尽管线性规划方法在稀疏重建方面有较好的理论基础，但由于其对峰值的“平滑化”处理，导致其在幅值恢复上有所欠缺，不能完全还原信号的实际幅值。

第二，ISTA和FISTA方法的重建效果存在显著差异。ISTA方法能够捕捉到信号的非零位置，但由于其收敛速度较慢，导致在有限的迭代次数下产生较多的噪声和波动；相比之下，FISTA作为ISTA的加速版本，其收敛更快，重建出的信号更接近真实稀疏信号的非零位置和幅值。因此，FISTA在准确性和效率上表现最佳。

---