LARS

最小角回归(LARS)

最小角回归（LARS）是一种用于高维数据稀疏回归的算法，由 Bradley Efron 和他的同事在 2004 年提出。本文将对其进行介绍

动机：在统计建模和机器学习中，随着数据维度的增加，传统的回归方法面临许多困难。尤其是当自变量（特征）数量远多于样本数量时（高维数据），标准的最小二乘回归会产生不稳定的估计，甚至导致过拟合。因此，为了构建一个稳定且具有较高解释性的模型，我们往往需要通过 特征选择 来挑选一小部分关键变量，从而得到一个稀疏的模型。

在这个背景下，LARS 被提出，以解决以下问题：

1.在高维数据中，LARS 逐步选择最相关的变量（特征）来降低模型的复杂度，避免过拟合。

2.相比传统的特征选择方法，LARS 提供了一种更高效的计算方式，特别适用于大规模数据。

3.LARS 与 Lasso 回归有一定的相似性，但 LARS 提供了一种更具解释性和连贯性的逐步回归路径，有助于理解特征选择的过程。

原理

LARS 的核心思想是逐步选择回归系数，逐渐将与响应变量最相关的特征“引入”模型。在这个过程中，LARS 遵循以下基本原则：

• 每一步选择与当前残差最相关的变量方向，将其引入模型。
• 每次向前移动一小步，直到另一个变量与残差的相关性达到相等，接着引入新的变量。
• LARS 的每一步都沿着最小角度前进，这样可以最大化对响应变量的解释力。

通过这种方式，LARS 建立了一个稀疏的模型路径，类似于 Lasso，但它通过一种更直观、逐步调整的方式实现了特征选择和回归系数估计。

下面，我们逐步探讨 LARS 算法的每一步操作及其背后的动机和理论基础。

首先，设定初始条件，将所有回归系数设为零，即 $\beta = 0 $， 初始化残差为响应变量 $ y $，即 $ r = y $，这一设定的动机在于，LARS 从“空模型”开始，逐步引入最相关的特征，从而使模型路径具备稀疏性和解释性。

其次，在每一轮迭代中，LARS 选择与当前残差$ r $ 具有最大相关性的特征，即找到与 $ r $ 的内积最大的特征：

\[X_j = \arg \max_j |X_j^T r| \]

这一步的目的是找到一个方向（即选择一个特征），该方向与当前残差最接近。这样做的原因是，为了最大程度地减少残差，选择一个与残差方向最接近的特征是最优的。

接下来，LARS 沿着选定的方向（对应于选中的特征）前进一小步。具体来说，LARS 通过调整系数 $ \beta_j $ 以缩小残差，并使其他未选择的特征与残差的相关性逐渐增加。具体地：

1. 沿着选择的方向增加系数 $ \beta_j $，以尽量减少残差。
2. 一旦另一个特征与残差的相关性达到相同程度（即形成一个小角度），则该特征被视为新的候选变量。

这一步的动机是保持一种“公平”的选择策略，即每次选择当前最相关的特征，并持续监控其他未选择特征的相关性，确保不会遗漏潜在重要的特征。

最后，一旦新的变量进入模型，LARS 会重新调整已选变量的系数，以确保当前所有选中变量的方向（即相关性）保持一致。这一步的目标是通过重新分配系数，沿着当前选择的所有变量方向共同前进，从而最大限度地减少残差。具体的数学形式是：

\[\beta_j = \arg \min \sum (y - X \beta)^2 \]

在这一点上，LARS 类似于一个逐步回归的过程，它在每次引入新变量后都会更新现有变量的系数，从而确保模型路径的平滑性。LARS 的停止条件通常是当所有变量都已进入模型，或者当增加任何变量都无法显著减少残差时停止。这样可以确保得到一个稀疏解，并且不包含多余的特征。

分析

LARS 的每一步都沿着最小角度前进，因此其名称 “最小角回归” 反映了这一关键特性。通过这种方法，LARS 在选择变量时不会“一步到位”地选择一个大系数，而是逐步增加系数值，从而减少选择变量的偏差。LARS 与 Lasso 回归有很深的联系。事实上，通过一些修改，LARS 可以生成与 Lasso 解相同的路径。这是因为 Lasso 也通过约束 $ l_1$ 范数最小化来实现稀疏解，而 LARS 提供了一个逐步逼近的视角，将这个约束过程转化为一个逐步的角度调整过程。

实验分析

下面这个中包含了数据生成、模型训练和绘图的过程，并重点测试了 LARS 的几个特点。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Lars, LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from matplotlib import rcParams

rcParams['font.sans-serif'] = ['SimHei']
rcParams['axes.unicode_minus'] = False

def generate_data(n_samples=100, n_features=50, noise_level=0.1, non_linear=False):
    np.random.seed(0)
    X = np.random.randn(n_samples, n_features)
    true_coef = np.zeros(n_features)
    true_coef[:5] = np.random.randn(5) * 10  
    y = X @ true_coef + noise_level * np.random.randn(n_samples)
    if non_linear:
        y = np.sin(y)  
    return X, y, true_coef

n_samples, n_features = 100, 50
noise_level = 0.1

X, y, true_coef = generate_data(n_samples=n_samples, n_features=n_features, noise_level=noise_level)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

lars = Lars(n_nonzero_coefs=5)
linear_reg = LinearRegression()

lars.fit(X_train, y_train)
y_pred_lars = lars.predict(X_test)

linear_reg.fit(X_train, y_train)
y_pred_linear = linear_reg.predict(X_test)

mse_lars = mean_squared_error(y_test, y_pred_lars)
mse_linear = mean_squared_error(y_test, y_pred_linear)

fig, axs = plt.subplots(2, 2, figsize=(14, 10), dpi=300)
fig.suptitle("LARS 算法的优势与局限", fontsize=16)

axs[0, 0].stem(true_coef, linefmt='b-', markerfmt='bo', basefmt=" ", label="真实系数")
axs[0, 0].stem(lars.coef_, linefmt='r--', markerfmt='ro', basefmt=" ", label="LARS估计系数")
axs[0, 0].set_title("LARS 稀疏性")
axs[0, 0].legend()
axs[0, 0].set_xlabel("特征索引")
axs[0, 0].set_ylabel("系数值")

axs[0, 1].plot(np.arange(len(y_test)), y_test, 'b-', label="真实值")
axs[0, 1].plot(np.arange(len(y_test)), y_pred_lars, 'r--', label="LARS预测值")
axs[0, 1].set_title("LARS 模型解释性")
axs[0, 1].legend()
axs[0, 1].set_xlabel("样本索引")
axs[0, 1].set_ylabel("预测值")

X_noisy, y_noisy, _ = generate_data(n_samples=n_samples, n_features=n_features, noise_level=0.5)
X_noisy_train, X_noisy_test, y_noisy_train, y_noisy_test = train_test_split(X_noisy, y_noisy, test_size=0.3, random_state=0)
X_noisy_train = scaler.fit_transform(X_noisy_train)
X_noisy_test = scaler.transform(X_noisy_test)
lars.fit(X_noisy_train, y_noisy_train)
y_noisy_pred = lars.predict(X_noisy_test)
axs[1, 0].plot(np.arange(len(y_noisy_test)), y_noisy_test, 'b-', label="真实值（含噪声）")
axs[1, 0].plot(np.arange(len(y_noisy_test)), y_noisy_pred, 'r--', label="LARS预测值（含噪声）")
axs[1, 0].set_title("LARS 对噪声的敏感性")
axs[1, 0].legend()
axs[1, 0].set_xlabel("样本索引")
axs[1, 0].set_ylabel("预测值")

X_nl, y_nl, _ = generate_data(n_samples=n_samples, n_features=n_features, noise_level=noise_level, non_linear=True)
X_nl_train, X_nl_test, y_nl_train, y_nl_test = train_test_split(X_nl, y_nl, test_size=0.3, random_state=0)
X_nl_train = scaler.fit_transform(X_nl_train)
X_nl_test = scaler.transform(X_nl_test)
lars.fit(X_nl_train, y_nl_train)
y_nl_pred = lars.predict(X_nl_test)
axs[1, 1].plot(np.arange(len(y_nl_test)), y_nl_test, 'b-', label="真实值（非线性）")
axs[1, 1].plot(np.arange(len(y_nl_test)), y_nl_pred, 'r--', label="LARS预测值（非线性）")
axs[1, 1].set_title("LARS 在非线性关系中的局限性")
axs[1, 1].legend()
axs[1, 1].set_xlabel("样本索引")
axs[1, 1].set_ylabel("预测值")

plt.tight_layout(rect=[0, 0.03, 1, 0.95])
plt.show()

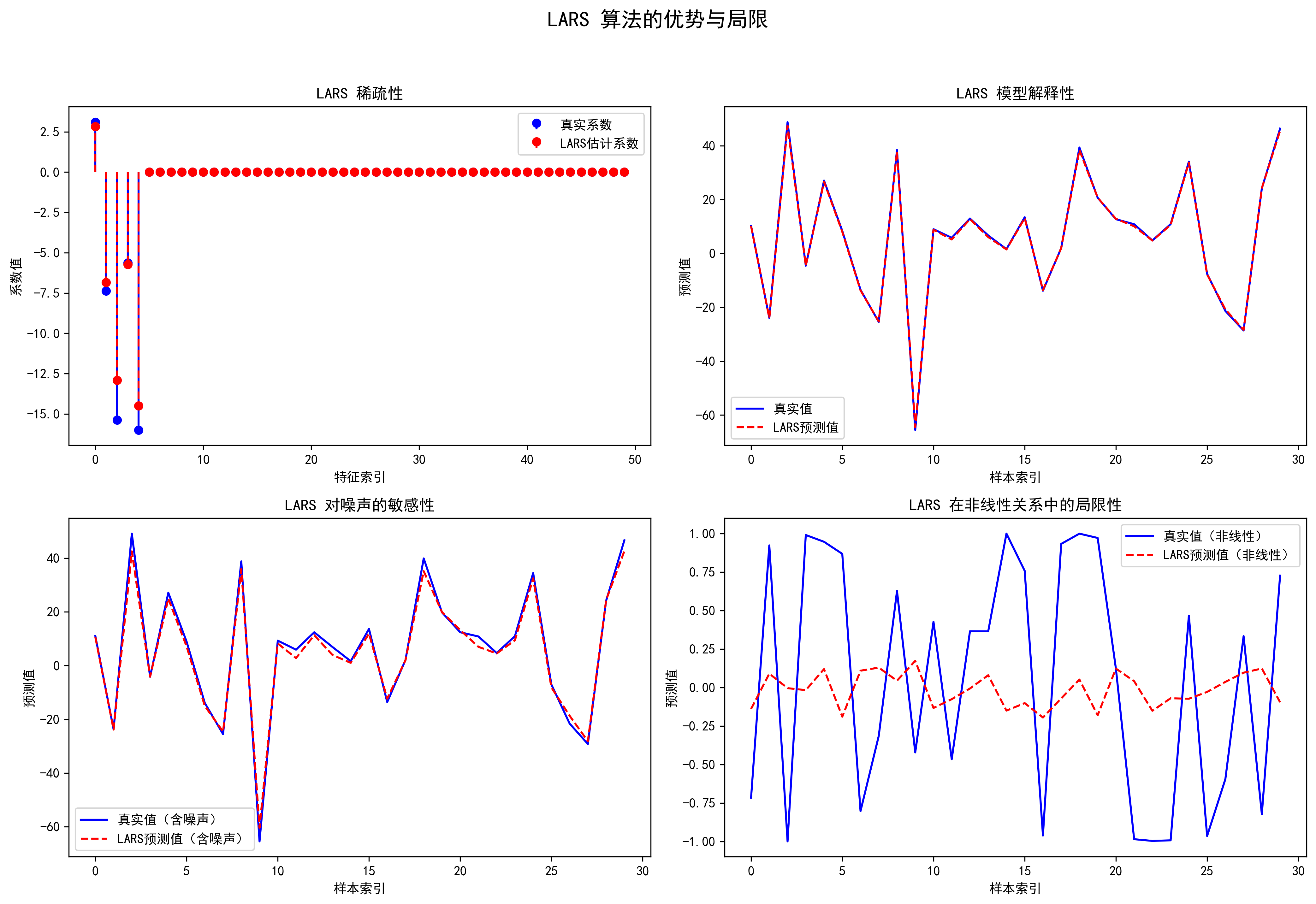
针对子图1，LARS 的估计系数集中在前几个特征上，并且其余大多数系数都接近于零。这一特点反映了 LARS 算法的稀疏性，即它只选择了少数几个对结果影响较大的特征，而忽略了其他噪声或无关特征。这种稀疏性使得 LARS 在处理高维数据时能够保持较低的模型复杂度，减少过拟合的风险，并有助于模型的可解释性。

针对子图2， LARS 的预测值和真实值在测试数据上的对比情况。从图中可以看出，LARS 的预测值与真实值的趋势非常接近，这说明 LARS 能够有效地捕捉到数据中的线性关系。在解释性方面，LARS 提供了一种逐步选择特征的路径，模型在每一步中引入新的特征，使得特征选择过程更为透明，便于解释每个特征引入的原因。这个图很好地展示了 LARS 模型在解释性方面的优势。

对于子图3，测试了 LARS 在较高噪声水平下的表现。可以看到，在加入较多噪声后，LARS 的预测值与真实值仍然有一定的吻合，但波动性明显增大，预测误差相对增加。这表明 LARS 算法在存在噪声的情况下会受到干扰，逐步引入噪声特征可能导致模型的准确性下降。因此，噪声敏感性是 LARS 的一大局限性。在数据预处理中，使用 LARS 前可能需要特别关注数据的噪声水平，并考虑适当的降噪方法。

第4个子图展示了 LARS 算法在非线性关系下的局限性。由于 LARS 是基于线性模型的假设，当数据中包含非线性关系时，它的表现不如线性情况下理想。从图中可以看到，LARS 的预测值无法很好地跟踪真实值的非线性波动，导致模型的误差较大。这表明，LARS 并不适用于复杂的非线性关系建模，需要在应用前确认数据的线性假设是否成立，否则可能需要引入其他适用于非线性问题的模型。

综合来看,LARS 算法在高维数据上计算效率高、具有稀疏性，并且提供了较强的模型解释性。但对噪声较为敏感，不适用于存在非线性关系的数据。

在实际应用中，可以根据数据特征来选择是否使用 LARS，必要时对数据进行降噪或特征转换，以改善模型表现。

附注

Bradley Efron 的人生思想体现了一种开放、实用和创新的态度。他相信统计学不仅是数学公式的演绎，更是一门服务于各个应用领域的科学。他的自助法和其他创新方法之所以被提出，是因为他始终坚持统计学要“帮助我们理解现实世界的复杂性”。不满足于传统统计方法的严格假设和局限性，而是致力于通过灵活、实用的方法，让统计学更好地适应和解释真实数据。因此，他的方法往往不拘泥于传统，却又极具实用性。

他的人生态度反映出他对“不断学习和探索”的信念。他认为统计学的发展永远是动态的，保持开放的心态去应对数据科学的变化。