F ISTA AND ISTA

ISTA and FISTA

迭代收缩阈值算法（ISTA）和快速迭代收缩阈值算法（FISTA）是处理稀疏信号重建和稀疏回归问题的两种重要算法。这两种算法常用于求解稀疏优化问题，例如解决带 $ l_1 $ 正则化的线性回归问题。本文将介绍这两种算法，从它们的提出背景、理论原理以及逐步改进的方式开始，一步步深入探讨。

在很多数据分析、信号处理等应用中，我们希望找到一种高效的方法来重建稀疏信号或选择重要特征。此类问题往往可以转化为优化问题，例如：

\[\min_{\beta} \frac{1}{2} \| y - X \beta \|_2^2 + \lambda \|\beta\|_1 \]

其中：

$ y $ 是响应向量，
$ X $ 是设计矩阵，
$ \beta $ 是待求的参数向量，
$ \lambda $ 是正则化参数，控制稀疏性。

目标是找到一个稀疏的 $ \beta $，即其中包含尽可能多的零元素。这类问题由于 $ l_1$ 正则项的存在，导致其不可微，传统的梯度下降法无法直接应用。因此，ISTA 应运而生。

迭代收缩阈值算法 (ISTA)

ISTA 的基本思想是：通过逐步优化的方式，每一步根据梯度信息更新当前的解，同时对解进行收缩处理，以实现 $ l_1 $ 正则化的效果。该算法的关键在于如何有效地对解进行“收缩”（即设置阈值，使小于阈值的解变为零）从而达到稀疏的效果。

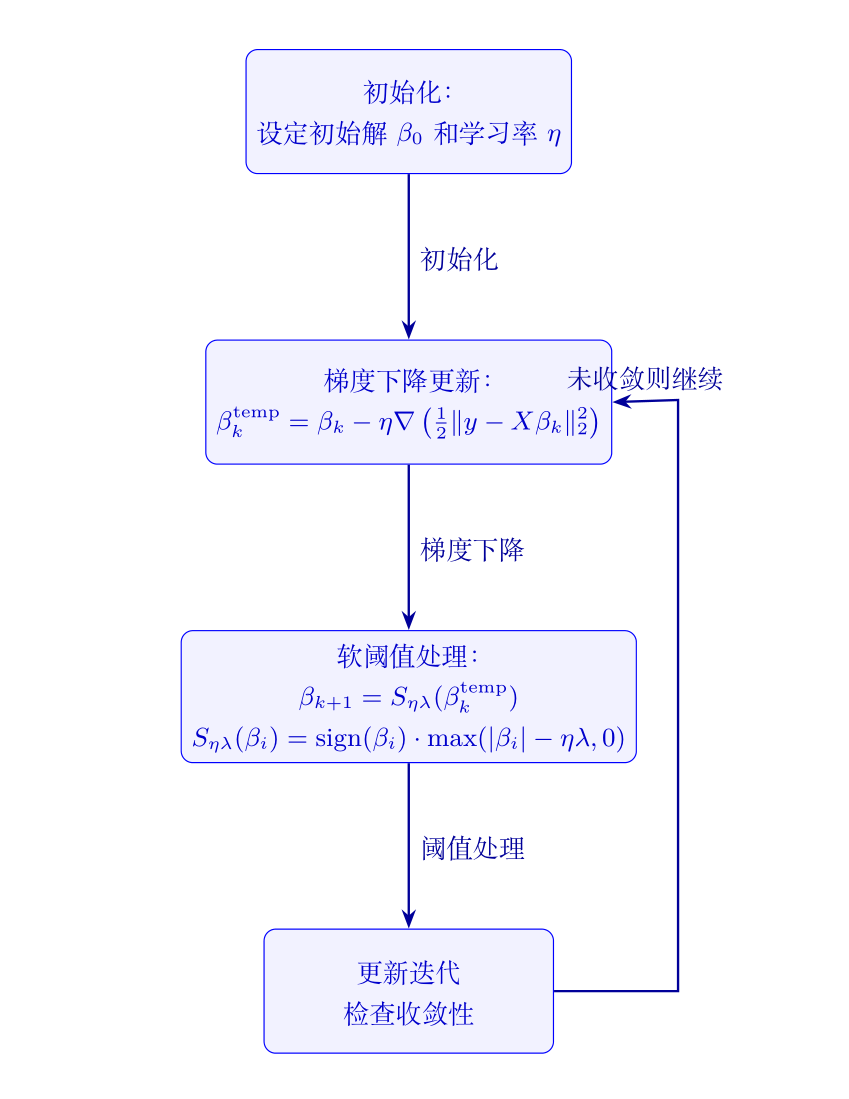
ISTA 的每次迭代可以分为两个主要步骤：梯度下降和软阈值处理。

梯度下降：对于光滑部分 $ \frac{1}{2} | y - X \beta |_2^2 $，我们可以利用梯度下降方法来更新当前的解。记当前的迭代解为 $ \beta_k $，则梯度下降更新可以表示为：

\[\beta_k^{\text{temp}} = \beta_k - \eta \nabla \left( \frac{1}{2} \| y - X \beta_k \|_2^2 \right) \]
其中 $ \eta $ 是学习率，通常选择一个小的常数值。这个更新相当于沿着损失函数下降最快的方向移动一步，以减小残差。
软阈值处理：由于我们希望得到稀疏解，梯度下降后的结果 $ \beta_k^{\text{temp}} $ 还需要进行一次收缩操作，以消除小于某个阈值的系数。这一步称为“软阈值处理”，定义为：

\[\beta_{k+1} = S_{\eta \lambda}(\beta_k^{\text{temp}}) \]
其中 $ S_{\eta \lambda} $ 是软阈值算子，即：

\[S_{\eta \lambda}(\beta_i) = \text{sign}(\beta_i) \cdot \max(|\beta_i| - \eta \lambda, 0) \]
这一操作使得较小的系数被直接置为零，较大的系数则被“收缩”，从而实现稀疏化效果。

ISTA 算法以这样的梯度下降和软阈值处理不断交替进行，每次迭代后，解 $\beta $ 会向稀疏方向逼近。由于每次只进行一步更新，因此 ISTA 的收敛速度较慢，尤其是在大规模数据上。因此，ISTA 虽然简单，但可能在实际应用中存在效率瓶颈。

快速迭代收缩阈值算法 (FISTA)

FISTA 是对 ISTA 的加速版本。其主要思路是在 ISTA 的基础上通过一种加速机制，使得每一步的迭代不仅依赖于当前的梯度信息，还参考了上一次迭代的信息。这种加速技术能够显著提升收敛速度，使得算法在较少的迭代次数下达到更优的解。

在 ISTA 中，每次迭代仅基于当前的解 $ \beta_k $ 和梯度信息来更新。然而，Nesterov 提出了一种加速梯度的方法，认为通过结合上一步的信息可以更快地逼近最优解。FISTA 采用了类似的加速策略，其更新规则不再是简单的梯度下降，而是：

\[\beta_k^{\text{temp}} = \beta_k + t_k (\beta_k - \beta_{k-1}) \]

其中 $ t_k $ 是一个加速参数，通过该参数可以实现对上一步的加权，进而加速收敛。具体地， $ t_k $ 通常取为：

\[t_k = \frac{1 + \sqrt{1 + 4 t_{k-1}^2}}{2} \]

为了证明 FISTA 中的加速参数 $ t_k $ 的选择可以有效加速收敛，我们首先需要理解 Nesterov 加速梯度方法的基本原理和其所带来的收敛性改进。

FISTA是基于 Nesterov 提出的加速方法构建的，因此，我们可以从能量下降速度的角度，逐步推导加速参数 $ t_k $ 的形式和它如何提高收敛性。

考虑一个凸优化问题：

\[\min_{\beta} f(\beta) \]

其中 $ f(\beta) $ 是一个凸函数。在 FISTA 中，目标是通过迭代的方式找到该函数的一个近似最优解，迭代更新的方式在每步上结合了当前解和前一步解的信息。

对于一个简单的梯度下降算法，每一步的更新方式为：

\[\beta_{k+1} = \beta_k - \eta \nabla f(\beta_k) \]

其中 $ \eta $ 是学习率。对于一些具有平滑性质的凸函数，这种方法的收敛速率为 $ O(1/k) $。虽然这种收敛速度可以保证找到最优解，但在高维数据和稀疏问题中，收敛速度仍然不够理想。

Nesterov 提出了一个加速的方法，通过在梯度下降更新中引入额外的动量项，使得更新过程能够更快地逼近最优解。具体地，通过加入上一次迭代信息的线性组合，实现“向前看”的更新方式，即考虑更多历史信息。

在 FISTA 中，这种加速方式的更新规则被写作：

\[\beta_k^{\text{temp}} = \beta_k + t_k (\beta_k - \beta_{k-1}) \]

其中 $ t_k $ 是一个加速参数。为了得到合适的 $ t_k$，FISTA 使用如下的递推关系：

\[t_k = \frac{1 + \sqrt{1 + 4 t_{k-1}^2}}{2} \]

为了得到这个递推关系，我们需要先定义一个能量函数的下降条件，并通过数学归纳法来证明该选择的合理性。

令 $ t_0 = 1 $。在每次迭代时，定义一个加速后的解为：

\[y_k = \beta_k + \left(\frac{t_{k-1} - 1}{t_k}\right) (\beta_k - \beta_{k-1}) \]

并令更新公式变为：

\[\beta_{k+1} = \text{prox}_{\eta \lambda} \left( y_k - \eta \nabla f(y_k) \right) \]

其中 $ \text{prox} $ 表示软阈值操作。

通过这种更新方式，Nesterov 加速法理论上可以达到 $ O(1/k^2) $ 的收敛速度。为了使得每一步都能满足这种加速效果，选择 $ t_k $ 满足以下方程：

\[t_k^2 - t_k - t_{k-1}^2 = 0 \]

这其实是一个二次方程，解为：

\[t_k = \frac{1 + \sqrt{1 + 4 t_{k-1}^2}}{2} \]

可以证明，当选择 $ t_k $ 满足上述递推公式时，整个算法的能量下降速率满足：

\[f(\beta_k) - f(\beta^*) = O\left(\frac{1}{k^2}\right) \]

这就意味着，通过选择适当的加速参数 $ t_k $，可以显著加快算法的收敛速度。这种加速的关键在于每步迭代的更新都能够“跳得更远”，而不是简单地沿着梯度下降方向。

在没有加速的情况下，梯度下降算法在每一步更新的距离较小，导致收敛速度慢。而通过 FISTA 的加速策略，加入前一步的信息，使得每一步能够以更大步长进行更新，同时保持稳定性，从而实现了 $ O(1/k^2) $ 的收敛速度。

因此，FISTA 的每次迭代包含以下几个主要步骤：

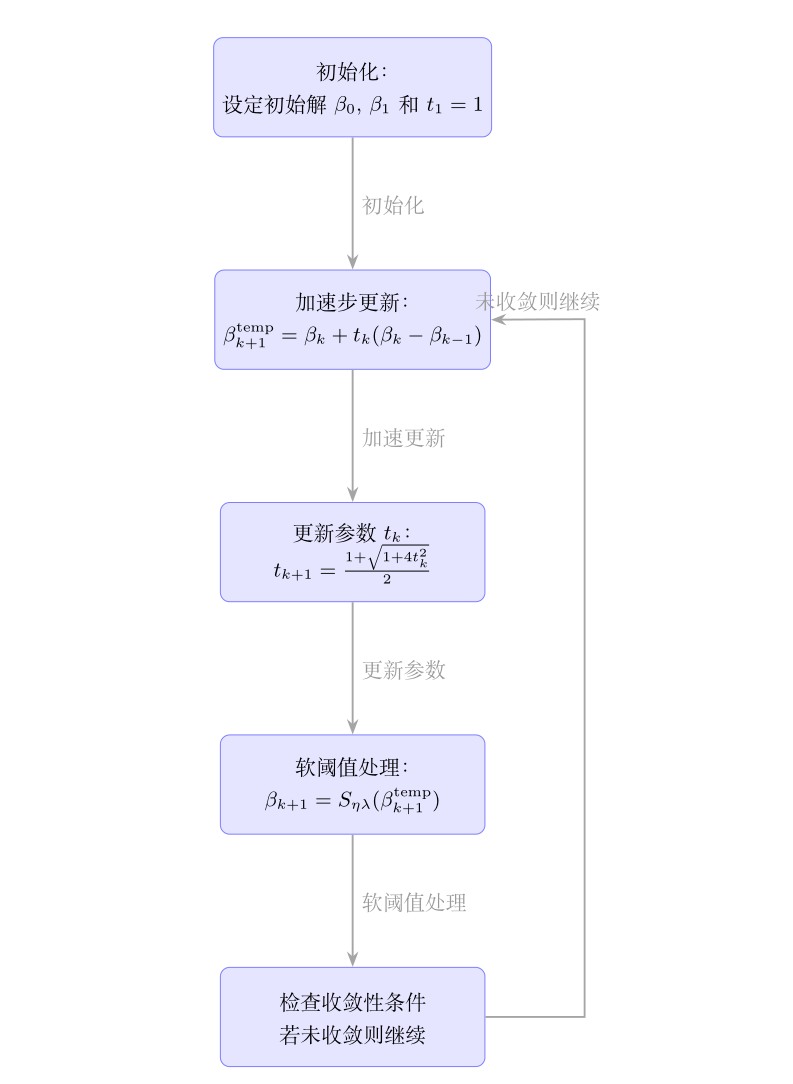
首先设置初始解 $\beta_0$, $\beta_1$ 和 $t_1 = 1$，FISTA 需要初始解 $\beta_0$ 和上一步解 $\beta_1$ 来进行加速更新。此外，$t_1$ 的初始值也设置为 1，是 FISTA 的标准设置。其次，为了在每一步中利用上一步解的信息，根据梯度更新的公式 $\beta_{k+1}^{\text{temp}} = \beta_k + t_k (\beta_k - \beta_{k-1})$
，从而加快收敛速度。进一步根据公式 $t_{k+1} = \frac{1 + \sqrt{1 + 4 t_k^2}}{2}$ 加速收敛，确保了在每次迭代中使用正确的加速参数 $t_k$，
“软阈值处理”节点中，$ \beta_{k+1} = S_{\eta \lambda}(\beta_{k+1}^{\text{temp}}) $ 是 ISTA 和 FISTA 算法的关键步骤之一。软阈值处理通过将值缩小到接近零的程度，实现了稀疏性的效果。最后检查收敛性条件，若收敛则结束，反之，则继续。

通过这样的加速和更新过程，FISTA 能够在较少的迭代次数下逼近稀疏解。

FISTA 的收敛速度要快于 ISTA。理论上，ISTA 的收敛速度为$ O(1/k) $，而 FISTA 的收敛速度则达到 $ O(1/k^2)$。这意味着 FISTA 能够在大规模数据中更有效地找到稀疏解，尤其适用于需要快速收敛的应用场景。

实验

下面主要比较 ISTA 和 FISTA 两种算法的性能，主要从收敛速度和稀疏解的质量上进行对比。

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
from sklearn.metrics import mean_squared_error

rcParams['font.sans-serif'] = ['SimHei']  
rcParams['axes.unicode_minus'] = False  
rcParams['figure.dpi'] = 300  

def generate_data(n_samples=100, n_features=50, sparsity=5, noise_level=0.1):
    np.random.seed(0)
    X = np.random.randn(n_samples, n_features)
    true_coef = np.zeros(n_features)
    indices = np.random.choice(n_features, sparsity, replace=False)
    true_coef[indices] = np.random.randn(sparsity) * 10
    y = X @ true_coef + noise_level * np.random.randn(n_samples)
    return X, y, true_coef

# ISTA算法
def ista(X, y, lambda_, eta, max_iter=1000, tol=1e-6):
    beta = np.zeros(X.shape[1])
    cost_history = []
    mse_history = []
    
    for i in range(max_iter):
        gradient = X.T @ (X @ beta - y)
        beta_temp = beta - eta * gradient
        beta = np.sign(beta_temp) * np.maximum(np.abs(beta_temp) - eta * lambda_, 0)
        cost = 0.5 * np.linalg.norm(y - X @ beta) ** 2 + lambda_ * np.sum(np.abs(beta))
        mse = mean_squared_error(true_coef, beta)
        
        cost_history.append(cost)
        mse_history.append(mse)
        
        if i > 0 and abs(cost_history[-2] - cost_history[-1]) < tol:
            break
    return beta, cost_history, mse_history

# FISTA算法
def fista(X, y, lambda_, eta, max_iter=1000, tol=1e-6):
    beta = np.zeros(X.shape[1])
    beta_old = beta.copy()
    t = 1
    cost_history = []
    mse_history = []
    
    for i in range(max_iter):
        gradient = X.T @ (X @ beta - y)
        beta_temp = beta - eta * gradient
        beta_new = np.sign(beta_temp) * np.maximum(np.abs(beta_temp) - eta * lambda_, 0)
        
        t_new = (1 + np.sqrt(1 + 4 * t ** 2)) / 2
        beta = beta_new + ((t - 1) / t_new) * (beta_new - beta_old)
        
        beta_old = beta_new
        t = t_new
        
        cost = 0.5 * np.linalg.norm(y - X @ beta) ** 2 + lambda_ * np.sum(np.abs(beta))
        mse = mean_squared_error(true_coef, beta)
        
        cost_history.append(cost)
        mse_history.append(mse)
        
        if i > 0 and abs(cost_history[-2] - cost_history[-1]) < tol:
            break
    return beta, cost_history, mse_history

n_samples, n_features, sparsity = 100, 50, 5
lambda_, eta = 0.1, 0.001
X, y, true_coef = generate_data(n_samples, n_features, sparsity)
beta_ista, cost_history_ista, mse_history_ista = ista(X, y, lambda_, eta)
beta_fista, cost_history_fista, mse_history_fista = fista(X, y, lambda_, eta)

fig, axs = plt.subplots(3, 2, figsize=(14, 15))
fig.suptitle("ISTA与FISTA算法对比", fontsize=16, weight='bold')

axs[0, 0].stem(true_coef, linefmt='b-', markerfmt='bo', basefmt=" ", label="真实系数")
axs[0, 0].stem(beta_ista, linefmt='r--', markerfmt='rs', basefmt=" ", label="ISTA估计系数")
axs[0, 0].stem(beta_fista, linefmt='g-.', markerfmt='g^', basefmt=" ", label="FISTA估计系数")
axs[0, 0].legend()
axs[0, 0].set_title("真实系数与估计系数对比", fontsize=12)
axs[0, 0].set_xlabel("特征索引", fontsize=10)
axs[0, 0].set_ylabel("系数值", fontsize=10)

axs[0, 1].plot(cost_history_ista, color='crimson', linestyle='-', label="ISTA收敛")
axs[0, 1].plot(cost_history_fista, color='mediumseagreen', linestyle='-', label="FISTA收敛")
axs[0, 1].legend()
axs[0, 1].set_title("损失函数收敛", fontsize=12)
axs[0, 1].set_xlabel("迭代次数", fontsize=10)
axs[0, 1].set_ylabel("损失值", fontsize=10)

axs[1, 0].plot(mse_history_ista, color='crimson', linestyle='-', label="ISTA均方误差")
axs[1, 0].plot(mse_history_fista, color='mediumseagreen', linestyle='-', label="FISTA均方误差")
axs[1, 0].legend()
axs[1, 0].set_title("均方误差 (MSE) 收敛", fontsize=12)
axs[1, 0].set_xlabel("迭代次数", fontsize=10)
axs[1, 0].set_ylabel("均方误差", fontsize=10)

non_zero_ista = np.sum(beta_ista != 0)
non_zero_fista = np.sum(beta_fista != 0)
axs[1, 1].bar(["ISTA", "FISTA"], [non_zero_ista, non_zero_fista], color=['crimson', 'mediumseagreen'])
axs[1, 1].set_title("稀疏性对比（非零系数数目）", fontsize=12)
axs[1, 1].set_ylabel("非零系数数目", fontsize=10)

axs[2, 0].plot(np.log10(cost_history_ista), color='crimson', linestyle='-', label="ISTA收敛速度")
axs[2, 0].plot(np.log10(cost_history_fista), color='mediumseagreen', linestyle='-', label="FISTA收敛速度")
axs[2, 0].legend()
axs[2, 0].set_title("收敛速度对比（对数刻度）", fontsize=12)
axs[2, 0].set_xlabel("迭代次数", fontsize=10)
axs[2, 0].set_ylabel("对数损失值", fontsize=10)

axs[2, 1].bar(["ISTA", "FISTA"], [len(cost_history_ista), len(cost_history_fista)], color=['crimson', 'mediumseagreen'])
axs[2, 1].set_title("计算时间（迭代次数）对比", fontsize=12)
axs[2, 1].set_ylabel("迭代次数", fontsize=10)

plt.tight_layout(rect=[0, 0, 1, 0.95])
plt.show()

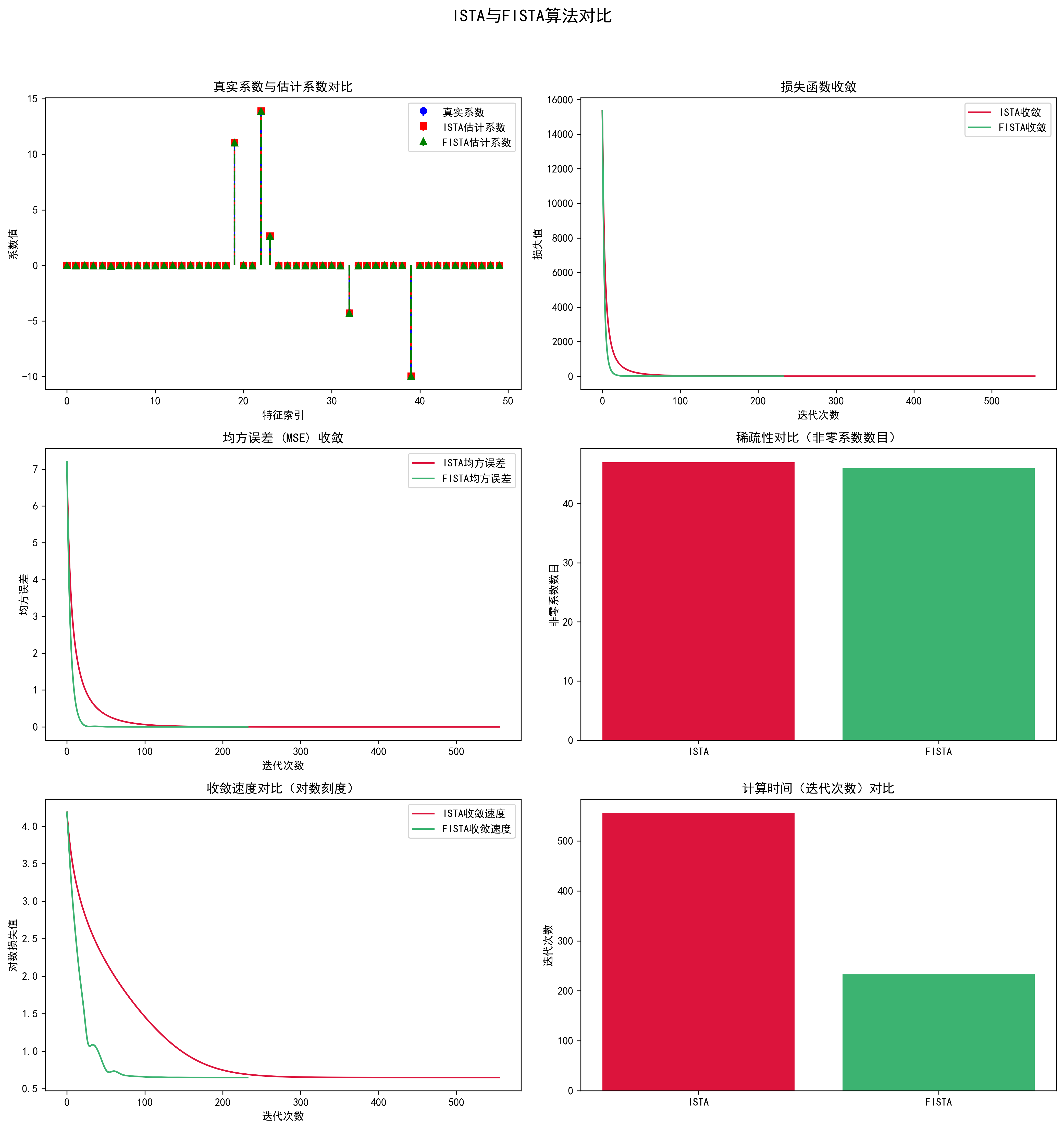
结果图3，首先，从损失函数收敛和均方误差（MSE）收敛曲线来看，FISTA比ISTA的收敛速度明显更快。在图中可以看到，FISTA的收敛曲线迅速下降，几乎在很少的迭代次数内就趋于稳定，而ISTA的下降较为缓慢。这验证了FISTA在收敛速度上的优势，使其更适合于大规模稀疏问题的求解。

其次，从稀疏性对比（非零系数数目）和计算时间（迭代次数）来看，FISTA依然表现优异。虽然两个算法最终获得的稀疏度接近，但FISTA用更少的迭代次数达到了相似的稀疏解。这表明FISTA不仅能够快速收敛，而且在稀疏性方面与ISTA相当，同时耗时更少。因此，FISTA在保持精度和稀疏性的情况下，大大减少了计算成本，显示出它在实际应用中的显著优势。

下面来分析ISTA和FISTA两个算法的参数

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Lasso
from scipy.linalg import norm

np.random.seed(0)
n_samples, n_features = 100, 50
X = np.random.randn(n_samples, n_features)
true_coef = np.zeros(n_features)
true_coef[:5] = np.random.randn(5) * 10  
y = X @ true_coef + 0.1 * np.random.randn(n_samples)

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['figure.dpi'] = 300

def ista(X, y, eta, lambd, max_iter=500):
    beta = np.zeros(X.shape[1])
    loss_history = []
    for i in range(max_iter):
        grad = X.T @ (X @ beta - y) 
        beta_temp = beta - eta * grad
        beta = np.sign(beta_temp) * np.maximum(np.abs(beta_temp) - eta * lambd, 0)  
        try:
            loss = 0.5 * norm(X @ beta - y)**2 + lambd * norm(beta, 1)
            loss_history.append(loss)
        except OverflowError:
            print("损失值爆炸")
            break
    return beta, loss_history

def fista(X, y, eta, lambd, max_iter=500):
    beta = np.zeros(X.shape[1])
    beta_prev = np.zeros(X.shape[1])
    t = 1
    loss_history = []
    for i in range(max_iter):
        grad = X.T @ (X @ beta - y)
        beta_temp = beta - eta * grad
        beta_new = np.sign(beta_temp) * np.maximum(np.abs(beta_temp) - eta * lambd, 0)
        t_new = (1 + np.sqrt(1 + 4 * t**2)) / 2
        beta = beta_new + ((t - 1) / t_new) * (beta_new - beta_prev)
        beta_prev = beta_new
        t = t_new
        try:
            loss = 0.5 * norm(X @ beta - y)**2 + lambd * norm(beta, 1)
            loss_history.append(loss)
        except OverflowError:
            print("损失值爆炸")
            break
    return beta, loss_history

etas = [0.001, 0.01, 0.1]
lambdas = [0.1, 0.5, 1.0]
max_iter = 500

fig, axs = plt.subplots(3, 3, figsize=(18, 12))
fig.suptitle("ISTA 与 FISTA 参数影响分析", fontsize=16)

for idx, eta in enumerate(etas):
    for jdx, lambd in enumerate(lambdas):
        # ISTA
        beta_ista, loss_ista = ista(X, y, eta, lambd, max_iter)
        axs[idx, jdx].plot(loss_ista, label=f"ISTA, η={eta}, λ={lambd}", color='blue', linestyle='--')
        
        # FISTA
        beta_fista, loss_fista = fista(X, y, eta, lambd, max_iter)
        axs[idx, jdx].plot(loss_fista, label=f"FISTA, η={eta}, λ={lambd}", color='green')
        
        axs[idx, jdx].set_title(f"学习率 η={eta} & 正则化 λ={lambd}")
        axs[idx, jdx].set_xlabel("迭代次数")
        axs[idx, jdx].set_ylabel("损失值")
        axs[idx, jdx].legend()
        axs[idx, jdx].grid()

plt.tight_layout(rect=[0, 0.03, 1, 0.95])
plt.show()

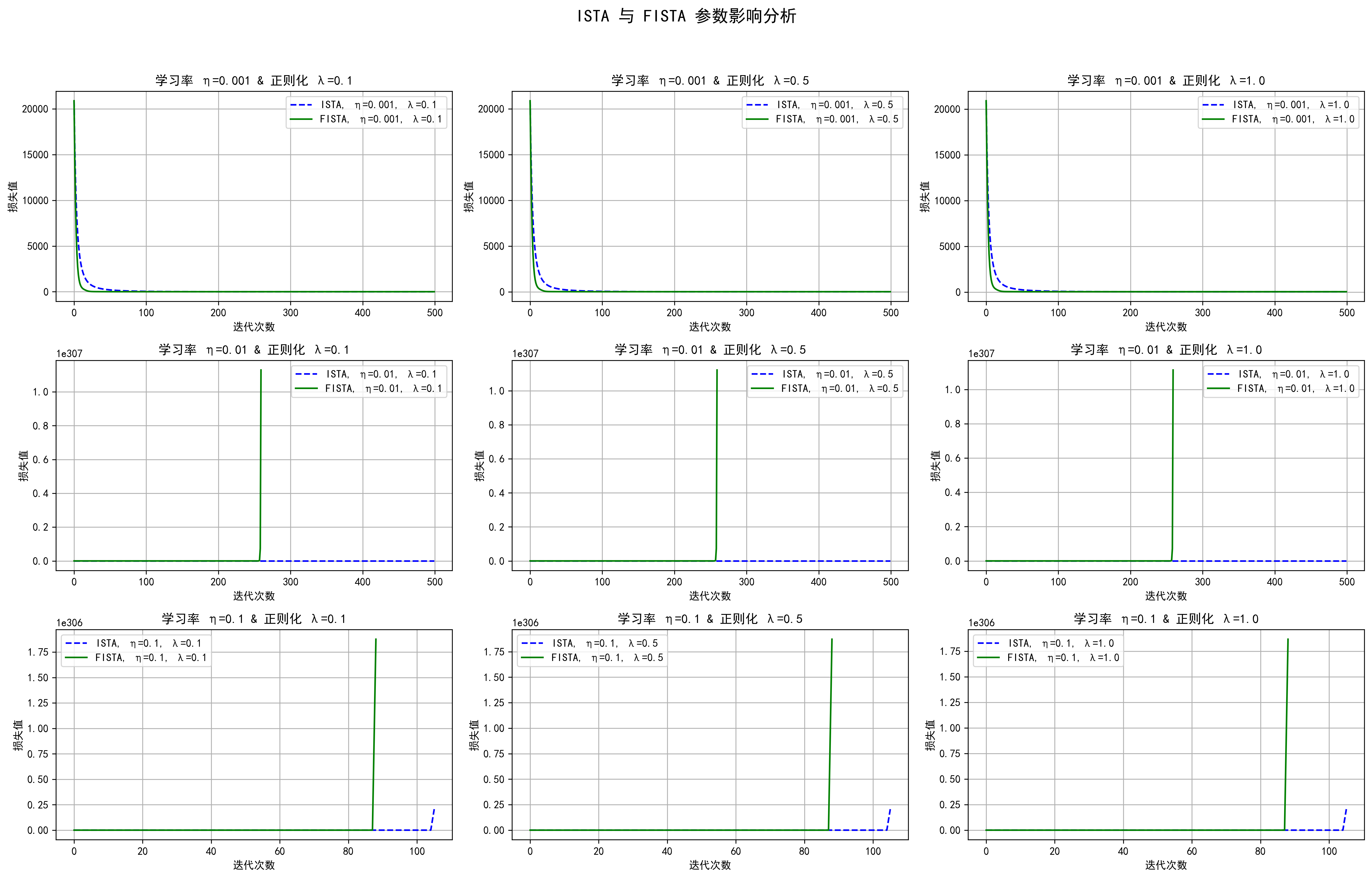
从图4中可以观察到以下几点：

收敛速度和收敛性：在第一行的图中，我们可以看到，对于较小的学习率（如 $\eta=0.001$ 和 $\eta=0.01$），ISTA 和 FISTA 都能稳定地收敛到较低的损失值。然而，在较大的学习率（如 $\eta=0.1$）下，FISTA 的收敛速度显著加快，但其迭代过程更容易出现溢出问题（损失值爆炸）。FISTA 的加速策略在提高收敛速度的同时也增大了数值计算的不稳定性，而 ISTA 在这种情况下更稳定但收敛速度较慢。
溢出情况的影响：溢出警告表明，在较高的学习率和正则化参数（如 $\eta=0.1$ 和 $\lambda=1.0$）下，FISTA 的加速更新策略使得迭代步幅过大，导致损失值爆炸。中间两行的图表进一步表明了溢出的影响，尤其是在 FISTA 算法中，损失值迅速增大，导致算法停止。这种现象表明，FISTA 对学习率和正则化参数更为敏感，需要更精确的参数调优，而 ISTA 在这种情况下表现更为稳健。

posted on 2024-12-05 10:52 咸鱼不翻身呀阅读(572) 评论(1) 收藏举报

刷新页面返回顶部

signal-opt

导航

公告

F ISTA AND ISTA

ISTA and FISTA