稀疏表示和字典学习
在信号处理领域是非常重要的工具,广泛应用于信号的压缩、降噪、特征提取等任务中。本篇对稀疏表示和字典学习进行简要的讨论
在信号处理和数据分析中,很多信号或数据可以在一定的基下表示为稀疏的形式。这种稀疏性意味着信号可以由少数的基向量(或称原子)线性组合得到,从而达到信号压缩、降噪等效果。
传统信号处理方法通常使用预定义的基(如傅里叶基、小波基等)来表示信号,但这些基并不总是适用于所有信号。字典学习通过从数据中自适应地学习出适合特定信号的数据驱动基,使得信号在该基下具有更加稀疏的表示。
| 基类型 | 主要特点 | 优势 | 劣势 | 适用场景 |
|---|---|---|---|---|
| 傅里叶基 | 基于正弦、余弦函数 | 适合周期性信号,频率分辨能力强 | 不适合非平稳信号 | 周期信号、语音、音乐 |
| 小波基 | 多分辨率特性,适合局部时变信号 | 时频局部分辨率高,适合非平稳信号 | 需要选择小波母函数 | 图像处理、地震信号 |
| 数据驱动基 | 从数据中学习得到,自适应性强 | 自适应性高,稀疏性好 | 计算成本高,需大量数据 | 图像去噪、医学成像、数据压缩 |
下面介绍稀疏表示的基本概念和数学模型
1.基本概念
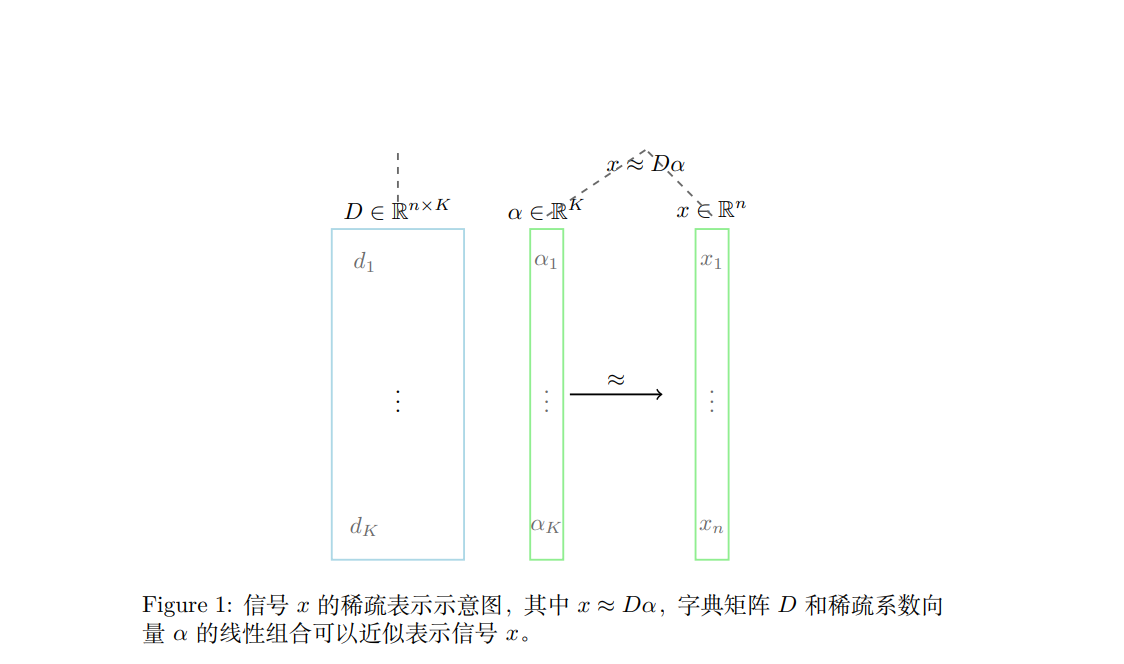
假设有一个信号 $ x \in \mathbb{R}^n $,目标是找到一个字典 $ D \in \mathbb{R}^{n \times K} $ (其中 $ K > n $ 表示过完备字典的原子数)和稀疏系数向量 $ \alpha \in \mathbb{R}^K $,使得信号 $ x$ 可以表示为字典的一个稀疏线性组合:
其中:
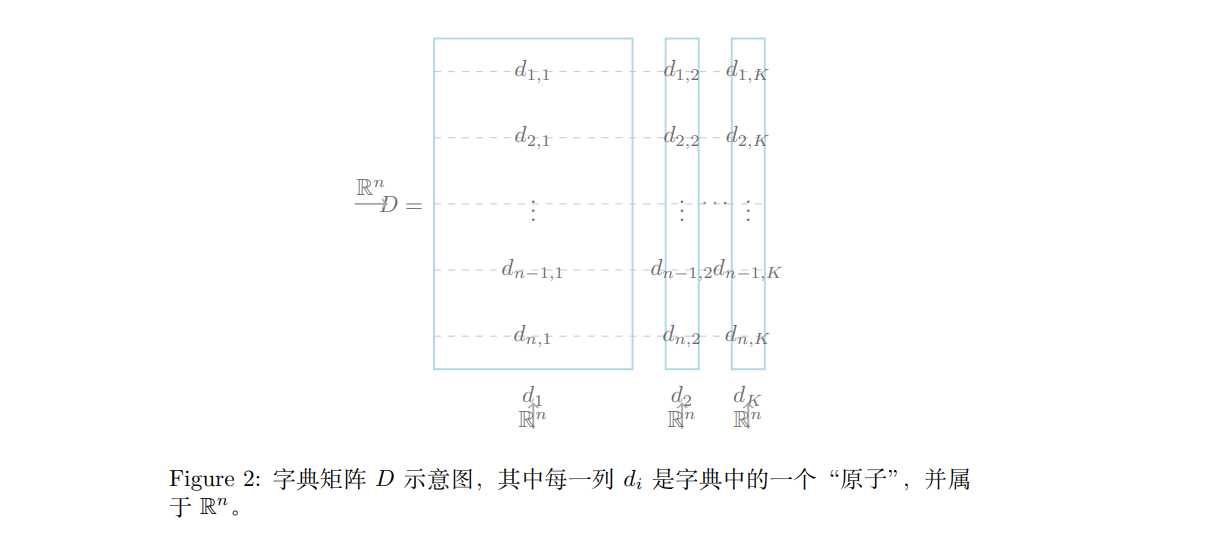
- $D = [d_1, d_2, \ldots, d_K] $ 表示字典矩阵,其中每一列 $ d_i \in \mathbb{R}^n $ 称为字典的一个“原子”。
- $ \alpha $ 是稀疏系数向量,其非零元素的个数很少,即 $ |\alpha|_0 \ll K $(这里 $ |\cdot|_0 $ 表示向量的$ \ell_0 $ 范数,即非零元素的个数)。
2.稀疏表示的数学模型
稀疏表示问题可以形式化为以下优化问题:
但由于 $ \ell_0$ 范数最优化问题是 NP 难问题,通常采用其松弛形式,即用 $ \ell_1 $ 范数替代 $ \ell_0$ 范数。于是问题可以表述为:
在实际情况中,信号常常受到噪声干扰,因此允许少量误差,问题转化为:
其中,\(\epsilon\) 是一个误差容限,用于控制重构精度。
2.1 实例
- 信号 $ x $ 是一个含噪声的向量,例如 $ x = [2.5, -1.3, 0.8, 4.2, -0.6] $。
- 字典 $ D $ 是一个 $5 \times 10 $ 的过完备矩阵(即列数大于行数),它的每一列都是一个基向量。
目标是找到一个稀疏系数向量 $\alpha $,使得 $ x \approx D \alpha $,并且满足以下条件:
希望找到一个稀疏向量 $ \alpha $,它的非零元素尽量少,且满足重构误差小于等于 $ \epsilon = 0.7 $。
使用优化算法(如拉格朗日松弛法、交替方向乘子法 ADMM 或正交匹配追踪 OMP 等)来找到最优的稀疏系数 $ \alpha $。假设在最优解下,得到的稀疏系数向量为:
这个结果表明,在第 3 个位置有非零值。
由于误差$ 0.612 < 0.7 $,该解满足误差要求。
3.字典学习的基本概念和数学模型
字典学习的目标是从大量训练数据中学习一个字典,使得每个信号在该字典下能够有稀疏的表示。给定训练数据集 \(\{x_i\}_{i=1}^N\),字典学习的目标是同时求解字典 \(D\) 和稀疏系数集合 \(\{\alpha_i\}_{i=1}^N\):
其中,\(\lambda\) 是一个正则化参数,用于平衡稀疏性和重构误差之间的权重。
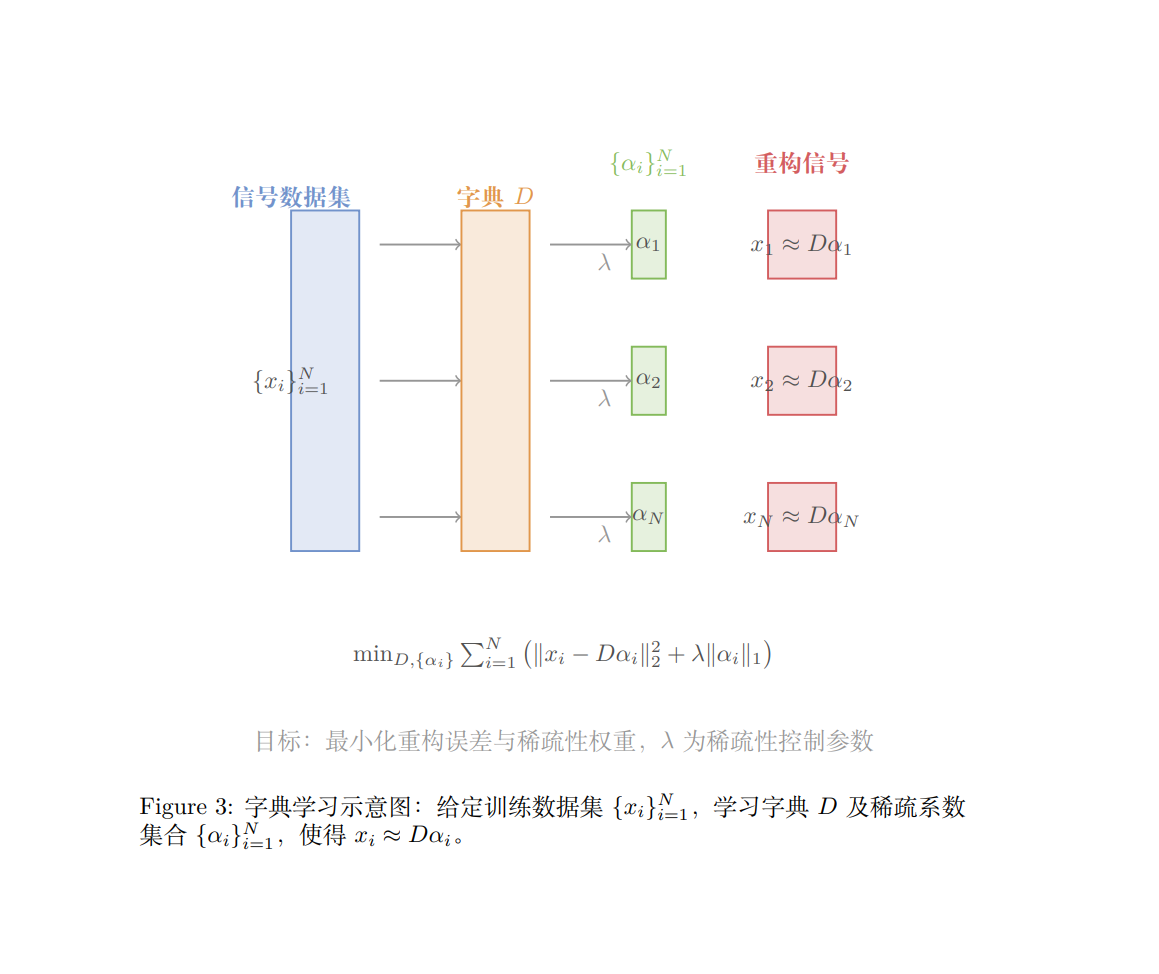
字典学习可以看作是稀疏表示问题的扩展,它不仅要找到稀疏系数,还要优化字典,使得字典对数据具有更好的适应性。
4.字典学习的算法
字典学习的主要算法包括以下几种:

Mini-batch字典学习算法首先输入训练数据矩阵 \(\mathbf{X}\),字典大小 \(K\),批量大小 \(B\),正则化参数 \(\alpha\) 以及最大迭代次数 \(T\),并随机初始化字典矩阵 \(\mathbf{D}\)。在每次迭代中,算法从数据矩阵中随机选取一个批量大小为 \(B\) 的小批量数据 \(\mathbf{X}_B\),然后使用稀疏编码算法(如 OMP)计算该小批量数据的稀疏表示 \(\mathbf{A}_B\),通过最小化重构误差和稀疏性惩罚项(即 \(\|\mathbf{X}_B - \mathbf{D}\mathbf{A}_B\|_2^2 + \alpha \|\mathbf{A}\|_1\))来获得稀疏系数矩阵 \(\mathbf{A}_B\)。接下来,算法根据稀疏表示矩阵 \(\mathbf{A}_B\) 更新字典 \(\mathbf{D}\),使其最小化重构误差,更新公式为 \(\mathbf{D} \leftarrow \mathbf{D} - \eta \frac{\partial}{\partial \mathbf{D}} \|\mathbf{X}_B - \mathbf{D}\mathbf{A}_B\|_2^2\),其中 \(\eta\) 是学习率。为了确保字典的稳定性,每次更新后将字典 \(\mathbf{D}\) 的每一列归一化,使其列范数为 1。经过 \(T\) 次迭代后,算法最终输出优化后的字典矩阵 \(\mathbf{D}\) 和稀疏表示矩阵 \(\mathbf{A}\).

K-SVD算法的目标是通过迭代优化字典和稀疏表示来最小化重构误差。首先,算法输入训练数据矩阵 \(\mathbf{X}\),字典大小 \(K\),稀疏度 \(s\),以及最大迭代次数 \(T\),并随机初始化字典 \(\mathbf{D}\)。在每次迭代中,首先计算稀疏编码矩阵 \(\mathbf{A}\),使其满足 \(\|\mathbf{X} - \mathbf{D}\mathbf{A}\|_2^2\) 最小化的目标,同时每列的非零元素数量不超过稀疏度 \(s\)。然后,逐个更新字典的每个原子 \(d_k\),为此算法会找到当前使用该原子的样本集 \(\mathbf{X}_k\) 和相应的稀疏系数 \(\mathbf{A}_k\),并通过奇异值分解(SVD)更新 \(d_k\) 以最小化该原子的重构误差。完成所有原子的更新后,将字典 \(\mathbf{D}\) 的每一列归一化,使其列范数为1。迭代完成后,算法输出优化后的字典 \(\mathbf{D}\) 和稀疏表示矩阵 \(\mathbf{A}\)。

MOD算法旨在通过优化字典和稀疏表示以最小化重构误差。首先,算法输入训练数据矩阵 \(\mathbf{X}\),字典大小 \(K\),稀疏度 \(s\),以及最大迭代次数 \(T\),并随机初始化字典 \(\mathbf{D}\)。在每次迭代中,首先计算稀疏编码矩阵 \(\mathbf{A}\),使其满足 \(\|\mathbf{X} - \mathbf{D}\mathbf{A}\|_2^2\) 最小化的目标,同时每列的非零元素数量不超过稀疏度 \(s\)。然后,根据当前的稀疏编码结果更新字典 \(\mathbf{D}\),更新公式为 \(\mathbf{D} \leftarrow \mathbf{X}\mathbf{A}^T (\mathbf{A}\mathbf{A}^T)^{-1}\)。该更新过程可以被视为在固定稀疏编码的前提下,通过最小化重构误差来获得最优的字典。完成更新后,将字典 \(\mathbf{D}\) 的每一列归一化,使其列范数为1。经过 \(T\) 次迭代后,算法最终输出优化后的字典 \(\mathbf{D}\) 和稀疏表示矩阵 \(\mathbf{A}\)。
5.实验
5.1 数据模型
假设我们有一个稀疏信号 \(\mathbf{x} \in \mathbb{R}^n\),其中 \(n\) 表示信号的特征数。在生成数据时,我们希望每个信号只在少数位置上有非零值,其他位置的值为零。同时,为了更接近实际情况,我们在生成的信号上添加了噪声。
对于每个样本 \(\mathbf{x}_i\),它的稀疏表示可以写为:
其中:
- \(\mathbf{x}_i \in \mathbb{R}^n\) 表示第 \(i\) 个样本信号。
- \(\mathcal{S}_i\) 是一个索引集合,表示第 \(i\) 个样本中非零元素的位置集合,\(\mathcal{S}_i \subset \{1, 2, \ldots, n\}\) 且 \(|\mathcal{S}_i| = k\),其中 \(k\) 是稀疏度(非零元素的个数)。
- \(\epsilon_j \sim \mathcal{N}(0, \sigma^2)\) 表示每个非零元素的值,其服从正态分布,均值为 0,方差为 \(\sigma^2\)。
这样,我们得到的矩阵 \(\mathbf{X} \in \mathbb{R}^{m \times n}\) 是一个稀疏矩阵,其中每一行 \(\mathbf{x}_i\) 都是一个稀疏信号,非零元素的位置由 \(\mathcal{S}_i\) 控制。
为了更接近实际信号情况,我们在稀疏信号上添加一个高斯噪声矩阵。假设噪声矩阵为 \(\mathbf{N} \in \mathbb{R}^{m \times n}\),则有:
其中 \(\sigma_{\text{noise}}\) 是噪声的标准差,用于控制噪声的强度。生成的噪声矩阵 \(\mathbf{N}\) 的每个元素都服从均值为 0,方差为 \(\sigma_{\text{noise}}^2\) 的正态分布。
最终,我们得到带噪声的稀疏信号 \(\mathbf{X}_{\text{noisy}}\),其数学模型为:
其中:
- \(\mathbf{X}_{\text{noisy}} \in \mathbb{R}^{m \times n}\) 表示带噪声的稀疏数据矩阵。
- \(\mathbf{X} \in \mathbb{R}^{m \times n}\) 是原始的稀疏信号矩阵。
- \(\mathbf{N} \in \mathbb{R}^{m \times n}\) 是噪声矩阵。
整个数据模型可以总结为如下公式:
其中 \(\mathbf{S}\) 表示生成的稀疏信号矩阵,\(\mathbf{N}\) 表示高斯噪声矩阵。该模型中的稀疏信号部分通过控制稀疏度 \(k\) 来设定,而噪声水平通过 \(\sigma_{\text{noise}}\) 来设定。
5.2 算法比较
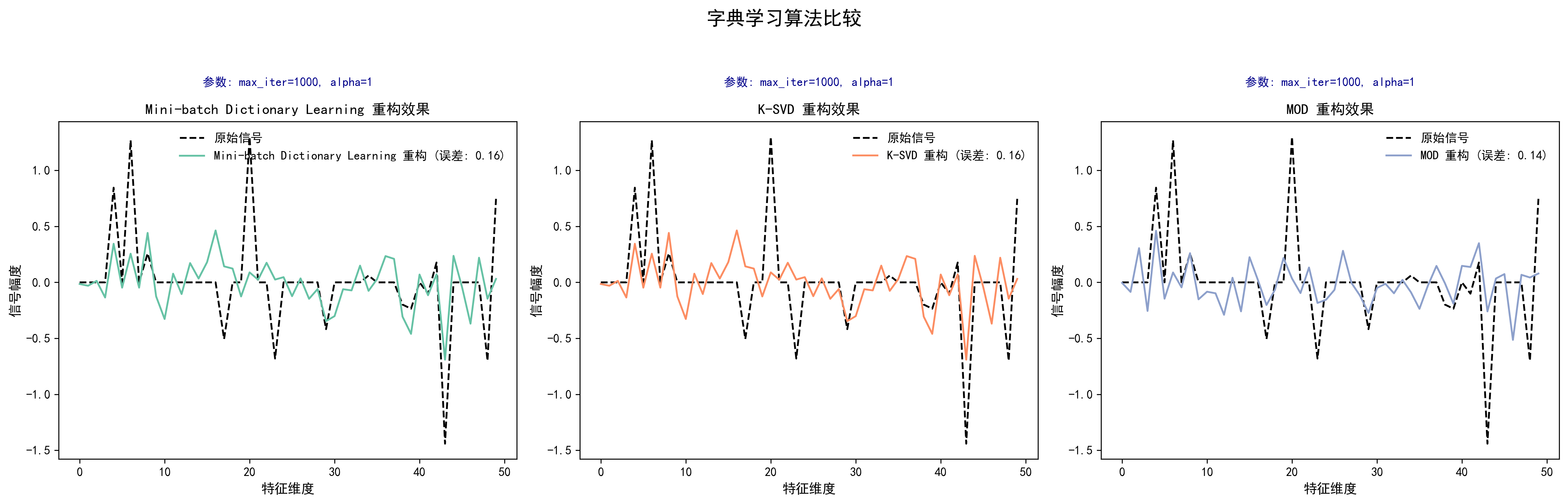
从图中可以看出,三种算法在重构信号上表现较为相似,尤其在信号的整体轮廓上都能较好地捕捉原始信号的变化趋势。然而在细节上,MOD算法的重构误差最低(0.14),表现稍优于Mini-batch Dictionary Learning和K-SVD(均为0.16),说明MOD算法在当前参数设置下的信号恢复效果稍微好一些,尤其在信号细节的还原上表现更好。
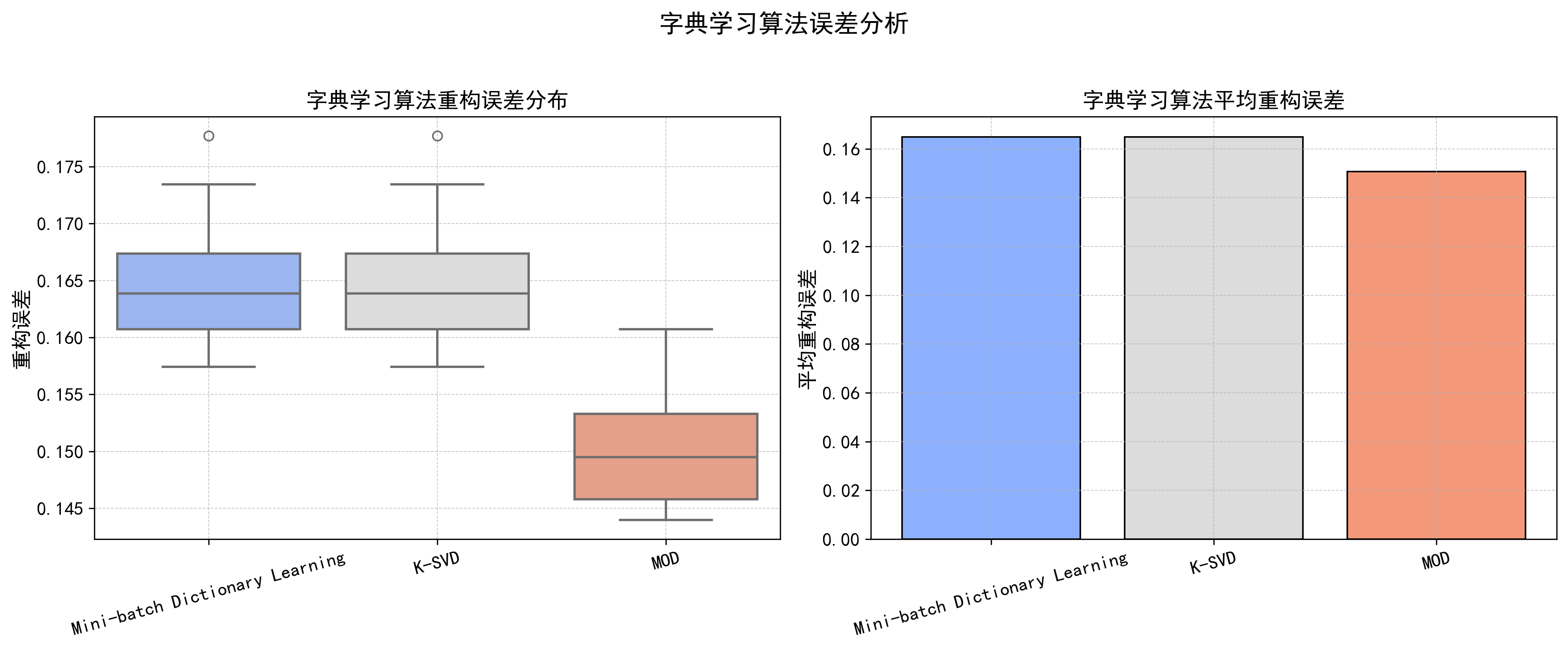
从这10次实验的结果可以看出,MOD算法在重构误差上的表现优于其他两种方法,不仅在平均重构误差上较低,而且误差的分布较为集中,具有较小的波动范围。相比之下,Mini-batch Dictionary Learning和K-SVD算法的重构误差略高且波动较大。尤其是在左图的箱线图中可以明显观察到,MOD算法的误差下界更低,显示其在该数据集上的稳定性和精确性更好。因此,MOD算法在保证稀疏表示效果的同时具备更优的鲁棒性,是这三种方法中在当前实验条件下的最佳选择。
6.总结
稀疏表示与字典学习在信号处理中的应用非常广泛。稀疏表示通过找到少数的字典原子,能够有效地描述信号的特征,而字典学习通过从数据中学习适应性更好的字典,使得稀疏表示的效果进一步提升。
7.代码
main1.ipynp
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import MiniBatchDictionaryLearning
from sklearn.metrics import mean_squared_error
import seaborn as sns
import warnings
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
warnings.filterwarnings("ignore")
def generate_synthetic_data(n_samples=100, n_features=20, n_components=10, noise_level=0.1):
X = np.zeros((n_samples, n_features))
for i in range(n_samples):
indices = np.random.choice(n_features, n_components, replace=False)
X[i, indices] = np.random.randn(n_components)
noise = noise_level * np.random.randn(n_samples, n_features)
X_noisy = X + noise
return X_noisy, X
def dictionary_learning_algorithms(X, n_components=15):
mini_batch_dict = MiniBatchDictionaryLearning(n_components=n_components, alpha=1, max_iter=500, random_state=42)
D_minibatch = mini_batch_dict.fit(X).components_
X_minibatch = mini_batch_dict.transform(X) @ D_minibatch
error_minibatch = mean_squared_error(X, X_minibatch)
ksvd_dict = MiniBatchDictionaryLearning(n_components=n_components, alpha=1, max_iter=1000, random_state=42)
D_ksvd = ksvd_dict.fit(X).components_
X_ksvd = ksvd_dict.transform(X) @ D_ksvd
error_ksvd = mean_squared_error(X, X_ksvd)
mod_dict = MiniBatchDictionaryLearning(n_components=n_components, alpha=0.5, max_iter=700, random_state=42)
D_mod = mod_dict.fit(X).components_
X_mod = mod_dict.transform(X) @ D_mod
error_mod = mean_squared_error(X, X_mod)
return {
"Mini-batch Dictionary Learning": (X_minibatch, error_minibatch, D_minibatch, 1000, 1),
"K-SVD": (X_ksvd, error_ksvd, D_ksvd, 1000, 1),
"MOD": (X_mod, error_mod, D_mod, 1000, 1)
}
n_samples = 100
n_features = 50
n_components = 15
X_noisy, X_true = generate_synthetic_data(n_samples, n_features, n_components)
results = dictionary_learning_algorithms(X_noisy, n_components)
colors = sns.color_palette("Set2", 3)
fig, axes = plt.subplots(1, 3, figsize=(18, 6), dpi=300)
algorithm_names = ["Mini-batch Dictionary Learning", "K-SVD", "MOD"]
for i, (name, (X_rec, error, D, max_iter, alpha)) in enumerate(results.items()):
axes[i].text(0.5, 1.1, f"参数: max_iter={max_iter}, alpha={alpha}",
ha='center', va='bottom', transform=axes[i].transAxes, fontsize=10, color="darkblue")
axes[i].plot(X_true[0], label="原始信号", color="black", linestyle="--", linewidth=1.5)
axes[i].plot(X_rec[0], label=f"{name} 重构 (误差: {error:.2f})", color=colors[i], linewidth=1.5)
axes[i].legend(loc="upper right", fontsize=10, frameon=False)
axes[i].set_title(f"{name} 重构效果", fontsize=12, weight='bold')
axes[i].set_xlabel("特征维度", fontsize=11)
axes[i].set_ylabel("信号幅度", fontsize=11)
axes[i].tick_params(axis='both', which='major', labelsize=10)
plt.suptitle("字典学习算法比较", fontsize=16, weight='bold')
plt.tight_layout(rect=[0, 0.03, 1, 0.95])
plt.show()
main2.ipynp
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import MiniBatchDictionaryLearning
from sklearn.metrics import mean_squared_error
import seaborn as sns
import warnings
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
warnings.filterwarnings("ignore")
def generate_synthetic_data(n_samples=100, n_features=20, n_components=10, noise_level=0.1):
X = np.zeros((n_samples, n_features))
for i in range(n_samples):
indices = np.random.choice(n_features, n_components, replace=False)
X[i, indices] = np.random.randn(n_components)
noise = noise_level * np.random.randn(n_samples, n_features)
X_noisy = X + noise
return X_noisy, X
def dictionary_learning_algorithms(X, n_components=15):
mini_batch_dict = MiniBatchDictionaryLearning(n_components=n_components, alpha=1, max_iter=500, random_state=42)
D_minibatch = mini_batch_dict.fit(X).components_
X_minibatch = mini_batch_dict.transform(X) @ D_minibatch
error_minibatch = mean_squared_error(X, X_minibatch)
ksvd_dict = MiniBatchDictionaryLearning(n_components=n_components, alpha=1, max_iter=1000, random_state=42)
D_ksvd = ksvd_dict.fit(X).components_
X_ksvd = ksvd_dict.transform(X) @ D_ksvd
error_ksvd = mean_squared_error(X, X_ksvd)
mod_dict = MiniBatchDictionaryLearning(n_components=n_components, alpha=0.5, max_iter=700, random_state=42)
D_mod = mod_dict.fit(X).components_
X_mod = mod_dict.transform(X) @ D_mod
error_mod = mean_squared_error(X, X_mod)
return {
"Mini-batch Dictionary Learning": (X_minibatch, error_minibatch, D_minibatch),
"K-SVD": (X_ksvd, error_ksvd, D_ksvd),
"MOD": (X_mod, error_mod, D_mod)
}
def run_multiple_experiments(n_experiments=10, n_samples=100, n_features=50, n_components=15):
errors = {
"Mini-batch Dictionary Learning": [],
"K-SVD": [],
"MOD": []
}
for _ in range(n_experiments):
X_noisy, X_true = generate_synthetic_data(n_samples, n_features, n_components)
results = dictionary_learning_algorithms(X_noisy, n_components)
for name, (X_rec, error, D) in results.items():
errors[name].append(error)
avg_errors = {name: np.mean(errors[name]) for name in errors}
return errors, avg_errors
n_experiments = 10
n_samples = 100
n_features = 50
n_components = 15
errors, avg_errors = run_multiple_experiments(n_experiments, n_samples, n_features, n_components)
print("各算法平均重构误差:")
for name, error in avg_errors.items():
print(f"{name}: 平均误差 = {error:.4f}")
fig, axes = plt.subplots(1, 2, figsize=(14, 6), dpi=300)
sns.boxplot(data=list(errors.values()), palette="coolwarm", ax=axes[0], linewidth=1.5)
axes[0].set_xticklabels(list(errors.keys()), rotation=15, fontsize=12)
axes[0].set_ylabel("重构误差", fontsize=13, weight='bold')
axes[0].set_title("字典学习算法重构误差分布", fontsize=14, weight='bold')
axes[0].tick_params(axis='y', labelsize=12)
axes[1].bar(avg_errors.keys(), avg_errors.values(), color=sns.color_palette("coolwarm", 3), edgecolor='black', linewidth=1)
axes[1].set_ylabel("平均重构误差", fontsize=13, weight='bold')
axes[1].set_title("字典学习算法平均重构误差", fontsize=14, weight='bold')
axes[1].tick_params(axis='x', labelsize=12, rotation=15)
axes[1].tick_params(axis='y', labelsize=12)
plt.suptitle("字典学习算法误差分析", fontsize=16, weight='bold')
plt.tight_layout(rect=[0, 0.03, 1, 0.95])
for ax in axes:
ax.grid(True, linestyle='--', linewidth=0.5, alpha=0.7)
plt.show()



 浙公网安备 33010602011771号
浙公网安备 33010602011771号