解题笔记-CodeForces-908C New Year and Curling

0 题面

C. New Year and Curling

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Carol is currently curling.

She has n disks each with radius r on the 2D plane.

Initially she has all these disks above the line y = 10100.

She then will slide the disks towards the line y = 0 one by one in order from 1 to n.

When she slides the i-th disk, she will place its center at the point (xi, 10100). She will then push it so the disk’s y coordinate continuously decreases, and x coordinate stays constant. The disk stops once it touches the line y = 0 or it touches any previous disk. Note that once a disk stops moving, it will not move again, even if hit by another disk.

Compute the y-coordinates of centers of all the disks after all disks have been pushed.

Input

The first line will contain two integers n and r (1 ≤ n, r ≤ 1 000), the number of disks, and the radius of the disks, respectively.

The next line will contain n integers x1, x2, ..., xn (1 ≤ xi ≤ 1 000) — the x-coordinates of the disks.

Output

Print a single line with n numbers. The i-th number denotes the y-coordinate of the center of the i-th disk. The output will be accepted if it has absolute or relative error at most 10 - 6.

Namely, let's assume that your answer for a particular value of a coordinate is a and the answer of the jury is b. The checker program will consider your answer correct if 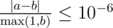 for all coordinates.

Example

input

6 2
5 5 6 8 3 12

output

2 6.0 9.87298334621 13.3370849613 12.5187346573 13.3370849613

Note

The final positions of the disks will look as follows:

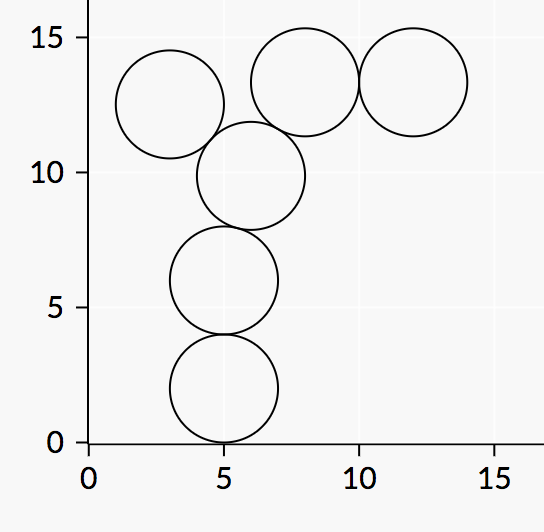
In particular, note the position of the last disk.

1 代码

#include <iostream>
#include <cmath>
#include <cstdio>
#define SQR(x) (x)*(x)
#define DIST(x, y) (SQR(x)+SQR(y))
#define ABS(x) ((x)>=0?x:(-x))
using namespace std;

int x[1000];
double y[1000];
int main()
{
    int n, r;
    cin >> n >> r;
    for(int i = 0; i < n; i++)
    {
        cin >> x[i];
    }
    for(int i = 0; i < n; i++)
    {
        int max_j = -1;
        double max_y = -1;
        double offset = 0;
        for(int j = 0; j < i; j++)
        {
            if((SQR(x[j] - x[i]) <= 4 * r * r) && ((y[j] + sqrt((double)(4.0 * r * r) - (double)(SQR(x[j] - x[i])))) > max_y))
            {
                max_j = j;
                max_y = (y[j] + sqrt((double)(4.0 * r * r) - (double)(SQR(x[j] - x[i]))));
            }
        }
        if(max_j == -1)
            y[i] = r;
        else
            y[i] = max_y;
    }
    for(int i = 0; i < n; i++)
    {
        printf("%.7f ", y[i]);
    }
}