网络流

网络流

　　记得我说过，除了树剖之外不再学超纲算法，然而今天我又...学了网络流。

　　Upd：联赛考完了，可以学了，咕咕咕。

　　学了Dinic算法，每次先做一次bfs求出是否还有增广路，再进行一次dfs看看最大的增广路是多少。对于每条边建一条容量为0的反向边，便于反悔。有的地方其实还不是很明白，以后再仔细想想。

首先是定义和性质：                                          

　　网络：网络是一种特殊的有向图，每条边带一个数字，叫做流量，意为从起点到终点最多通过$n$的单位的流。两个特殊的点，源点S，从这里可以运出无限的流；汇点T,流最后都会到这里来。

　　最大流：从源点到汇点最多可以运送的流量。

　　割：如果将图上割去一些边可以使得源点汇点不连通，那么这些边所构成的集合叫做一个割；

　　最小割：所有的割中流量和最小的那个。

　　最大流的三个性质：

　　　　容量限制:$f(u,v)<=c(u,v)$.

　　　　斜对称性:$f(u,v)=-f(v,u)$.

　　　　流量平衡:除了源汇节点,每个点的流入量和流出量相同.

　　至于这三个性质有什么用...我也不清楚...

　　最小割最大流定理：

　　　　最大流=最小割，证明：

　　　　刚刚机房停电了！！！我写好的一长段都没了啊啊啊啊啊啊

　　　　首先最小割不能小于最大流，否则无法将最大流割断。

　　　　其次最大流中的每个流量至少会经过一条满流的边，否则可以沿着这条路线再加流，只要把这些边都割断就可以达到割的目的了，所以最小割可以等于最大流。

　　　　综上所述最大流等于最小割。

　　费用流：每条边还有一个附加权表示每从这条边上运一个流所需要付出的代价。

　　最小费用最大流：在最大流的基础上费用最小。

接下来是板子：                                                                                      

　　

　　网络最大流：https://www.luogu.org/problemnew/show/P3376

　　

// luogu-judger-enable-o2
# include <cstdio>
# include <iostream>
# include <queue>
# include <cstring>
# define R register int
# define inf 1e8

const int maxn=20009;
int u,v,w,n,m,s,t,h=1,firs[maxn],d[maxn];
bool vis[maxn];
std::queue <int> q;
struct edge
{
    int too,nex,cap,flow;    
}g[1000009];

int min(int a,int b)
{
    if(a<b) return a;
    return b;
}

int read()
{
    int x=0;
    char c=getchar();
    while (!isdigit(c))
        c=getchar();
    while (isdigit(c))
    {
        x=(x<<3)+(x<<1)+(c^48);
        c=getchar();
    }
    return x;
}

void add(int x,int y,int v)
{
    g[++h].too=y;
    g[h].nex=firs[x];
    firs[x]=h;
    g[h].cap=v;
    g[h].flow=0;
}

bool bfs()
{
    memset(vis,0,sizeof(vis));
    while (q.size()) q.pop();
    q.push(s);
    d[s]=0;
    vis[s]=true;
    int beg,j;
    while (q.size())
    {
        beg=q.front();
        q.pop();
        for (R i=firs[beg];i;i=g[i].nex)
        {
            j=g[i].too;
            if(g[i].cap<=g[i].flow) continue;
            if(vis[j]) continue;
            vis[j]=true;
            d[j]=d[beg]+1;
            q.push(j);
        }
    }
    return vis[t];
}

int dfs(int x,int minf)
{
    if(x==t||minf==0) return minf;
    int j,flow=0,f;
    for (R i=firs[x];i;i=g[i].nex)
    {
        j=g[i].too;
        if(d[j]!=d[x]+1) continue;
        f=dfs(j,min(minf,g[i].cap-g[i].flow));
        if(f<=0) continue;
        g[i].flow+=f;
        g[i^1].flow-=f;
        minf-=f;
        flow+=f;
        if(minf==0) break;
    }
    return flow;
}

int maxflow()
{
    int ans=0;
    while (bfs())
        ans+=dfs(s,inf);
    return ans;
}

int main()
{
    scanf("%d%d%d%d",&n,&m,&s,&t);
    for (R i=1;i<=m;++i)
    {
        u=read(),v=read(),w=read();
        add(u,v,w);
        add(v,u,0);
    }
    printf("%d",maxflow());
    return 0;
}

 　　

　　最小费用最大流：https://www.luogu.org/problemnew/show/P3381

　　似乎都用EK写的，还没有见过Dinic的版本，那就跟风一回好了。其实就是把BFS增广改成了最短路增广。

　　

# include <cstdio>
# include <iostream>
# include <cstring>
# include <queue>
# define R register int
# define inf 999999999

using namespace std;

const int maxn=5005;
const int maxm=50005;
int n,m,s,t,x,y,w,co,h=1,min_cos,flow,pre[maxn],d[maxn],Fl[maxn];
bool in_que[maxn],vis[maxn];
queue <int> q;
int firs[maxn];
struct edge
{
    int too,nex,cap,flow,co;
}g[maxm<<1];

int read()
{
    int x=0;
    char c=getchar();
    while (!isdigit(c))
        c=getchar();
    while (isdigit(c))
    {
        x=(x<<3)+(x<<1)+(c^48);
        c=getchar();
    }
    return x;
}

void add (int x,int y,int cap,int co)
{
    g[++h].too=y;
    g[h].cap=cap;
    g[h].co=co;
    g[h].nex=firs[x];
    firs[x]=h;
}

bool bfs ()
{
    memset(vis,0,sizeof(vis));
    memset(d,0x3f,sizeof(d));
    memset(in_que,0,sizeof(in_que));
    vis[s]=true;
    d[s]=0;
    int j,beg;
    Fl[s]=inf;
    q.push(s);
    while (q.size())
    {
        beg=q.front();
        q.pop();
        in_que[beg]=false;
        for (R i=firs[beg];i;i=g[i].nex)
        {
            j=g[i].too;
            if(g[i].cap<=g[i].flow) continue;
            if(d[j]<=d[beg]+g[i].co) continue;
            vis[j]=true;
            d[j]=d[beg]+g[i].co;
            Fl[j]=min(Fl[beg],g[i].cap-g[i].flow);
            pre[j]=i;
            if(!in_que[j]) q.push(j),in_que[j]=true;
        }
    }
    return vis[t];
}

void dfs ()
{
    int x=t;
    while (x!=s)
    {
        int i=pre[x];
        g[i].flow+=Fl[t];
        g[i^1].flow-=Fl[t];
        x=g[i^1].too;
    }
    flow+=Fl[t];
    min_cos+=d[t]*Fl[t];
}

void maxflow()
{
    while (bfs())
        dfs();
}

int main()
{
    scanf("%d%d%d%d",&n,&m,&s,&t);
    for (R i=1;i<=m;++i)
    {
        x=read(),y=read(),w=read(),co=read();
        add(x,y,w,co);
        add(y,x,0,-co);
    }
    maxflow();
    printf("%d %d",flow,min_cos);
    return 0;
}

 

还有一些常用的套路：                                                                                

　　多源多汇：建立超级源点和汇点，向所有的源汇连流量为正无穷的边。

　　点限流：每个点拆成出点和入点，之间连接流量为点限度的边。

　　有一些东西其实已经可以出成题考建模技巧了，但是由于适用范围比较广，往往被当做模板来用...

　　网络流的推广：

　　一般所说的网络流中，每条边只有一个流量上界，但是也可以将它认为是带有流量下界且下界为0的一种特殊情况。

　　带上下界的循环流看了一小时了也没懂，先看一个简单一点的。

　　满足供需关系的可行流：每个点有一个权 $w(x)$ ,之前的流量平衡条件改为 出=入+$w(x)$ ，这个问题可以这样考虑，将权为正的点认为是凭空多出来 $w(x)$ 的流量，对于权为负数的点，将 $w(x)$ 的流量消掉，这样还是满足流量平衡。问题转化到这里就变成了一个多源多汇问题。如果存在一种方案使得附加边全部满流即存在可行流。

　　形式化的讲（配合后面的格式），

　　$$w(i)=\sum_{(i,j)\in E}f(i,j)-\sum_{(j,i)\in E}f(j,i)$$

　　我现在明白网络流三条看起来很显然的性质的作用了，就是用来以此为根据调整建图策略。

　　非常神奇的是这个算法可以转化为循环流：

​ 　　---以下内容摘自《习题指导》

　　$$\sum_{(i,j)\in E} f(i,j)-\sum_{(j,i)\in E}f(j,i) =0\quad \forall i \in V $$

　　$$b(i,j)<=f(i,j)<=c(i,j) \quad \forall i \in V$$

　　这是上下界网络流的定义；

　　既然我们不会处理下界，不如定义一个新的函数，通过变换消掉下界，$g(i,j)=f(i,j)-b(i,j)$

　　$$\sum_{(i,j)\in E} g(i,j)-\sum_{(j,i)\in E}g(j,i)=\sum_{(j,i)\in E} b(j,i)-\sum_{(i,j)\in E} b(i,j) \quad \forall i \in V $$

　　$$0<=g(i,j)<=c(i,j)-b(i,j) \quad \forall i \in V$$

　　这时候可以发现，虽然等式左边还是未知量，但是等式右边已经是一个常数了呀，和上一道题的权没有什么区别。于是就可以做了，真的好神奇啊。如果没有看懂也没关系，下面还有讲。

　　费用与流量有关的费用流：拆边，进行边权差分...还是举个例子吧:

　　

　　像这样边权不固定的问题是比较难办的,但是由于流量上界比较小,可以拆边:

　　

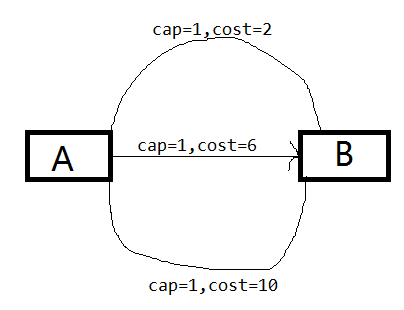
　　因为求的是最小费用,必然是第一个流量走上面那条边,越靠后的流量走边权越大的边,达到了所需要的效果.

　　套路先说这么多,做一点题再补.

最后来看一些题：                                                                                     

　　

　　1.负载平衡：https://www.luogu.org/problemnew/show/P4016

　　题意概述：G公司有n个沿铁路运输线环形排列的仓库，每个仓库存储的货物数量不等。如何用最少搬运量可以使n个仓库的库存数量相同。搬运货物时，只能在相邻的仓库之间搬运。

　　其实就是环形的均分纸牌。

　　感觉我的建图挺正常的，但是网上好像都不是这么建的...

　　弄一个源点向每个仓库连边，流量为原数量，费用为0；(因为本来就在那里嘛）

　　每个仓库向汇点连边，流量为平均数，费用为0；(也就是说要达到最大流必须每个点都弄到平均数个货物)

　　相邻的仓库连一下边，流量无限，费用为1;(自己随便传去吧)

　　

// luogu-judger-enable-o2
# include <cstdio>
# include <iostream>
# include <cstring>
# include <queue>
# define R register int
# define inf 999999999

using namespace std;

const int maxn=105;
const int maxm=409;
int n,m,s,t,x,y,w,co,h=1,min_cos,flow,pre[maxn],d[maxn],Fl[maxn];
long long S=0;
bool in_que[maxn],vis[maxn];
queue <int> q;
int firs[maxn];
struct edge
{
    int too,nex,cap,flow,co;
}g[maxm<<1];

int read()
{
    int x=0;
    char c=getchar();
    while (!isdigit(c))
        c=getchar();
    while (isdigit(c))
    {
        x=(x<<3)+(x<<1)+(c^48);
        c=getchar();
    }
    return x;
}

void add (int x,int y,int cap,int co)
{
    g[++h].too=y;
    g[h].cap=cap;
    g[h].co=co;
    g[h].nex=firs[x];
    firs[x]=h;
}

bool bfs ()
{
    memset(vis,0,sizeof(vis));
    memset(d,0x3f,sizeof(d));
    memset(in_que,0,sizeof(in_que));
    vis[s]=true;
    d[s]=0;
    int j,beg;
    Fl[s]=inf;
    q.push(s);
    while (q.size())
    {
        beg=q.front();
        q.pop();
        in_que[beg]=false;
        for (R i=firs[beg];i;i=g[i].nex)
        {
            j=g[i].too;
            if(g[i].cap<=g[i].flow) continue;
            if(d[j]<=d[beg]+g[i].co) continue;
            vis[j]=true;
            d[j]=d[beg]+g[i].co;
            Fl[j]=min(Fl[beg],g[i].cap-g[i].flow);
            pre[j]=i;
            if(!in_que[j]) q.push(j),in_que[j]=true;
        }
    }
    return vis[t];
}

void dfs ()
{
    int x=t;
    while (x!=s)
    {
        int i=pre[x];
        g[i].flow+=Fl[t];
        g[i^1].flow-=Fl[t];
        x=g[i^1].too;
    }
    flow+=Fl[t];
    min_cos+=d[t]*Fl[t];
}

void maxflow()
{
    while (bfs())
        dfs();
}

int main()
{
    scanf("%d",&n);
    t=n+1;
    for (int i=1;i<=n;++i)
    {
        x=read();
        S+=x;
        add(s,i,x,0);
        add(i,s,0,0);
        if(i==n) continue;
        add(i,i+1,inf,1);
        add(i+1,i,0,-1);
        add(i+1,i,inf,1);
        add(i,i+1,0,-1);
    }
    add(n,1,inf,1);
    add(1,n,0,-1);
    add(1,n,inf,1);
    add(n,1,0,-1);
    for (int i=1;i<=n;++i)
        add(i,t,S/n,0),add(t,i,0,0);
    maxflow();
    printf("%d",min_cos);
    return 0;
}

 

　　2.拍照:https://www.luogu.org/problemnew/show/P3410

　　神题一道，神题一道。其实也是个套路题，只不过没见过的时候觉得非常难想。

　　题意概述：给定m个集合，每个集合中包含n个元素中的一些。如果某个集合中的元素被全选，会有一个收益，选每个元素也会有各自的花费，求最大收益。$n,m<=100$

　　看到这么小的数据范围就觉得是dp，似乎可以bitset强行状压一番，然而这是不行的...统计答案也挺麻烦的。

　　其实这是一种网络流的模型：最大权闭合子图；

　　从这道题其实可以看出来一个很显然的事情，一个集合的收益可以获得，当且仅当它里面的元素全被选。（这话说出来怎么这么像机翻）

　　先连一下图，再看为什么：

　　对于每一个集合，建一个虚点，从源点向它连一条流量为收益的边；这个虚点向集合中的每个元素连一条流量为inf的边；每个元素向汇点连一条流量为花费的边，求最小割。

　　为什么？首先假设每个集合的收益都可以被获得，再考虑哪些收益不拿更优。这个图是一个挺明显的四层图：

　　

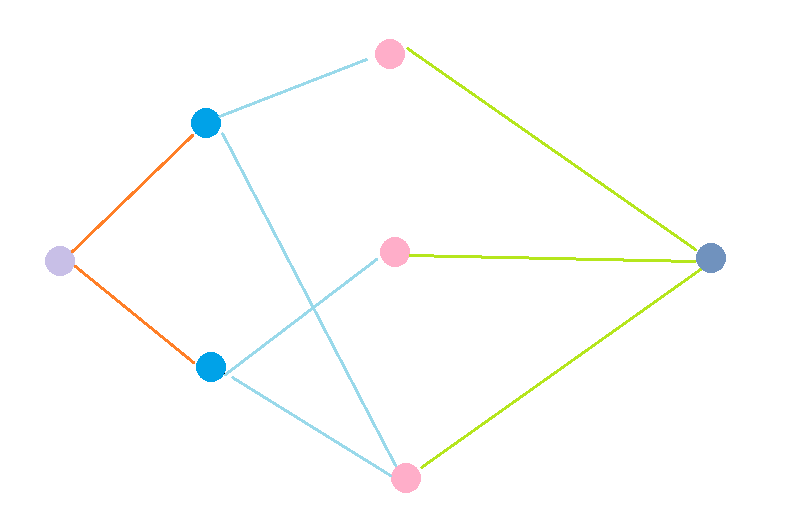
　　假设被留下的东西连在s，不选的连在t。那么想要把图变得不连通，就要求浅蓝色的点必须选择一方，有两种方案：

　　·把橙色边割断，表示不要这个收益了。

　　·把它发出去的所有绿色边割断，表示它涉及的所有粉色点都选。

　　浅蓝色的边是不能碰的，因为集合里有哪些元素不是我们能够左右的...这样我倒是又想到一道题：可以花费$c_i$的代价把某个点从某个集合中去掉，这样这个边也有边权了，不过这个题好像也没啥意思。

　　答案即为总收益减去最小割。注意前向星的h要从1开始...

　　

# include <cstdio>
# include <iostream>
# include <queue>
# include <cstring>
# define R register int
# define inf 0x7FFFFFFF

using namespace std;

int s,t,n,h=1,m,co,x,ans;
bool vis[205];
int firs[205],d[205];
queue <int> q;
struct edge
{
    int too,nex,flow,cap;
}g[30000];

void add (int x,int y,int co)
{
    g[++h].too=y;
    g[h].nex=firs[x];
    firs[x]=h;
    g[h].cap=co;
    g[h].flow=0;
}

bool bfs()
{
    memset(vis,0,sizeof(vis));
    q.push(s);
    d[s]=0;
    vis[s]=true;
    int beg,j;
    while (q.size())
    {
        beg=q.front();
        q.pop();
        for (R i=firs[beg];i;i=g[i].nex)
        {
            j=g[i].too;
            if(g[i].cap<=g[i].flow) continue;
            if(vis[j]) continue;
            vis[j]=true;
            d[j]=d[beg]+1;
            q.push(j);
        }
    }
    return vis[t];
}

int dfs (int x,int minf)
{
    if(x==t||minf==0) return minf;
    int j,flow=0,f;
    for (R i=firs[x];i;i=g[i].nex)
    {
        j=g[i].too;
        if(d[j]!=d[x]+1) continue;
        f=dfs(j,min(minf,g[i].cap-g[i].flow));
        if(f<=0) continue;
        g[i].flow+=f;
        g[i^1].flow-=f;
        minf-=f;
        flow+=f;
        if(minf==0) break;
    }
    return flow;
}

int maxflow()
{
    int flow=0;
    while (bfs())
        flow+=dfs(s,inf);
    return flow;
}

int main()
{
    scanf("%d%d",&m,&n);
    s=0,t=n+m+1;
    for (R i=1;i<=m;++i)
    {
        scanf("%d%d",&co,&x);
        add(s,i+n,co);
        add(i+n,s,0);
        ans+=co;
        while (x)
        {
            add(i+n,x,inf);
            add(x,i+n,0);
            scanf("%d",&x);
        }
    }
    for (R i=1;i<=n;++i)
    {
        scanf("%d",&x);
        add(i,t,x);
        add(t,i,0);
    }
    printf("%d",ans-maxflow());
    return 0;
}

　　

　　3.太空飞行计划问题：https://www.luogu.org/problemnew/show/P2762

　　题意概述：和上边那个题几乎一样，但是还要输出方案。

　　输出方案简直毒瘤啊。不过其实思路非常妙。从刚刚的解题思路考虑，其实最后保留下来的点都是可以从s到达的，也就是...那个vis数组...

　　

# include <cstdio>
# include <iostream>
# include <queue>
# include <cstring>
# include <algorithm>
# define R register int
# define inf 0x7fffffff

using namespace std;

int s,t,n,h=1,m,co,x,ans;
bool vis[105];
int firs[105],d[105],sta[105],Top=0;
queue <int> q;
struct edge
{
    int too,nex,flow,cap;
}g[30000];

void add (int x,int y,int co)
{
    g[++h].too=y;
    g[h].nex=firs[x];
    firs[x]=h;
    g[h].cap=co;
    g[h].flow=0;
}

bool bfs()
{
    memset(vis,0,sizeof(vis));
    while (q.size()) q.pop();
    q.push(s);
    d[s]=0;
    vis[s]=true;
    int beg,j;
    while (q.size())
    {
        beg=q.front();
        q.pop();
        for (R i=firs[beg];i;i=g[i].nex)
        {
            j=g[i].too;
            if(g[i].cap<=g[i].flow) continue;
            if(vis[j]) continue;
            vis[j]=true;
            d[j]=d[beg]+1;
            q.push(j);
        }
    }
    return vis[t];
}

int dfs (int x,int minf)
{
    if(x==t||minf==0) return minf;
    int j,flow=0,f;
    for (R i=firs[x];i;i=g[i].nex)
    {
        j=g[i].too;
        if(d[j]!=d[x]+1) continue;
        f=dfs(j,min(minf,g[i].cap-g[i].flow));
        if(f<=0) continue;
        g[i].flow+=f;
        g[i^1].flow-=f;
        minf-=f;
        flow+=f;
        if(minf==0) break;
    }
    return flow;
}

int maxflow()
{
    int flow=0;
    while (bfs())
        flow+=dfs(s,inf);
    return flow;
}

int main()
{
    scanf("%d%d",&m,&n);
    s=0,t=n+m+1;
    for (R i=1;i<=m;++i)
    {
        scanf("%d",&co);
        add(s,i+n,co);
        add(i+n,s,0);
        ans+=co;
        char tools[10000];
        memset(tools,0,sizeof tools);
        cin.getline(tools,10000);
        int ulen=0,tool;
        while (sscanf(tools+ulen,"%d",&tool)==1)
        {
            add(i+n,tool,inf);
            add(tool,i+n,0);
            if (tool==0) 
                ulen++;
            else 
            {
                   while (tool) 
                {
                    tool/=10;
                    ulen++;
                }
            }
            ulen++;
        }
    }
    for (R i=1;i<=n;++i)
    {
        scanf("%d",&x);
        add(i,t,x);
        add(t,i,0);
    }
    int mf=maxflow();
    for (R i=n+1;i<=n+m;++i)
        if(vis[i]) sta[++Top]=i-n;
    for (R i=1;i<Top;++i)
        printf("%d ",sta[i]);
    printf("%d",sta[Top]);
    printf("\n");
    Top=0;
    for (R i=1;i<=n;++i)
        if(vis[i]) sta[++Top]=i;
    for (R i=1;i<Top;++i)
        printf("%d ",sta[i]);
    printf("%d",sta[Top]);
    printf("\n");
    printf("%d",ans-mf);
    return 0;
}

 　　

　　4.电影迷:https://www.luogu.org/problemnew/show/P3872

　　题意概述：看电影,有的电影可以带来正的体验,有的可以带来负的,有的电影之间有联系,如果看了一部而没看另一部就会有负的体验值,求最高体验值.

　　直觉上好像只需要选收益为正的?然而不是,有时候可能你明明知道这个电影很难看,但是因为看过好看的上一部就特别想看一下,这时如果不看会带来更差的体验,所以贪心是不行的,考虑网络流.

　　答案初始化为所有正权值的和，网络流求出的是在这个基础上的最小损失。首先设立源汇，S表示要看，T表示不看。将正体验的电影与源点连容量为权值的边，负体验的与汇点连容量为权值相反数的边。对于依赖关系，从依赖的一方向被依赖的连边，容量为依赖值。求最小割，再用刚刚求出的答案减一下就是最终答案了。解释一下：对于一组体验值一正一负的电影，想分离ST有三种方法：割断S连出的边->放弃正体验电影，割断两者之间的边->只看正体验的，损失依赖值，割断T的边->两个都看，加上负体验（减去负体验的相反数）。

　　

# include <cstdio>
# include <iostream>
# include <cstring>
# include <queue>
# define  R register int
# define inf 1000000000

using namespace std;

const int maxn=105;
int n,m,s,t,h=1,ans,x,y,z;
int a[maxn],firs[maxn],d[maxn],vis[maxn];
queue <int> q;
struct edge
{
    int too,nex,flow,cap;
}g[500005];

void add (int x,int y,int co)
{
    g[++h].nex=firs[x];
    firs[x]=h;
    g[h].too=y;
    g[h].cap=co;
    g[++h].nex=firs[y];
    firs[y]=h;
    g[h].too=x;
}

bool bfs ()
{
    memset(vis,0,sizeof(vis));
    vis[s]=1;
    q.push(s);
    int beg,j;
    while(q.size())
    {
        beg=q.front();
        q.pop();
        for (R i=firs[beg];i;i=g[i].nex)
        {
            j=g[i].too;
            if(vis[j]) continue;
            if(g[i].cap<=g[i].flow) continue;
            d[j]=d[beg]+1;
            vis[j]=true;
            q.push(j);
        }
    }
    return vis[t];
}

int dfs (int s,int minf)
{
    if(s==t||minf==0) return minf;
    int flow=0,f,j;
    for (R i=firs[s];i;i=g[i].nex)
    {
        j=g[i].too;
        if(d[j]!=d[s]+1) continue;
        f=dfs(j,min(minf,g[i].cap-g[i].flow));
        if(f<=0) continue;
        minf-=f;
        flow+=f;
        g[i].flow+=f;
        g[i^1].flow-=f;
        if(minf==0) break;
    }
    return flow;
}

int maxflow()
{
    int ans=0;
    while(bfs()) ans+=dfs(s,inf);
    return ans;
}

int main()
{
    scanf("%d%d",&n,&m);
    s=0,t=n+1;
    for (R i=1;i<=n;++i)
    {
        scanf("%d",&a[i]);
        if(a[i]>0) add(s,i,a[i]),ans+=a[i];
        else add(i,t,-a[i]);
    }
    for (R i=1;i<=m;++i)
    {
        scanf("%d%d%d",&x,&y,&z);
        add(x,y,z);
    }
    printf("%d",max(ans-maxflow(),0));
    return 0;
}

 

　　5.蜥蜴：https://www.lydsy.com/JudgeOnline/problem.php?id=1066

　　题意概述：略。

　　如果点有最多经过次数，可以将它拆成一个出点一个入点，中间连上容量为最多经过次数的边。

　　

// luogu-judger-enable-o2
# include <cstdio>
# include <iostream>
# include <cstring>
# include <queue>
# include <string>
# include <queue>
# define inf 10000009
# define R register int

using namespace std;

const int maxn=41;
int ans,n,m,D,s,t,cnt,h=1;
char st[100];
int id[maxn][maxn][2],a[maxn][maxn],firs[maxn*maxn],d[maxn*maxn],vis[maxn*maxn],cur[maxn*maxn];
struct edge
{
    int too,nex,cap;
}g[maxn*maxn*200];
queue <int> q;
int ab (int x) { if(x<0) return -x; return x; }
int dis (int a,int b,int c,int d) { return ab(a-c)+ab(b-d); }

void add (int x,int y,int cap)
{
    g[++h].nex=firs[x];
    g[h].too=y;
    firs[x]=h;
    g[h].cap=cap;
    g[++h].nex=firs[y];
    g[h].too=x;
    firs[y]=h;
    g[h].cap=0;
}

bool bfs()
{
    memset(vis,0,sizeof(vis));
    q.push(s);
    int beg,j;
    vis[s]=true;
    while(q.size())
    {
        beg=q.front();
        q.pop();
        for (R i=firs[beg];i;i=g[i].nex)
        {
            j=g[i].too;
            if(vis[j]) continue;
            if(g[i].cap<=0) continue;
            d[j]=d[beg]+1;
            vis[j]=true;
            q.push(j);
        }
    }
    return vis[t];
}

int dfs (int x,int minf)
{
    if(minf==0||x==t) return minf;
    int flow=0,f,j;
    for (int& i=cur[x];i;i=g[i].nex)
    {
        j=g[i].too;
        if(d[j]!=d[x]+1) continue;
        f=dfs(j,min(minf,g[i].cap));
        if(f<=0) continue;
        g[i].cap-=f;
        g[i^1].cap+=f;
        flow+=f;
        minf-=f;
        if(minf==0) break;
    }
    return flow;
}

void init() { for (R i=0;i<=cnt;++i) cur[i]=firs[i]; }

int dinic()
{
    int ans=0;
    while(bfs())
    {
        init();
        ans+=dfs(s,inf);
    }
    return ans;
}

int main()
{
    scanf("%d%d%d",&n,&m,&D);
    s=0;
    for (R i=1;i<=n;++i)
        for (R j=1;j<=m;++j)
            scanf("%1d",&a[i][j]),id[i][j][0]=++cnt;
    for (R i=1;i<=n;++i)
        for (R j=1;j<=m;++j) id[i][j][1]=++cnt;
    t=++cnt;
    for (R i=1;i<=n;++i)
        for (R j=1;j<=m;++j)
        {
            if(a[i][j]==0) continue;
            add(id[i][j][0],id[i][j][1],a[i][j]);
            if(i<=D||j<=D||n-i+1<=D||m-j+1<=D) 
                add(id[i][j][1],t,inf);
        }
    for (R i=1;i<=n;++i)
    {
        scanf("%s",st+1);
        for (R j=1;j<=m;++j)
            if(st[j]=='L') add(s,id[i][j][0],1),ans++;
    }
    for (R i=1;i<=n;++i)
        for (R j=1;j<=m;++j)
        {
            if(a[i][j]==0) continue;
            for (R k=1;k<=n;++k)
                for (R z=1;z<=m;++z)
                {
                    if(i==k&&j==z) continue;
                    if(dis(i,j,k,z)>D) continue;
                    if(a[k][z]==0) continue;
                    add(id[i][j][1],id[k][z][0],inf);
                }
        }
    printf("%d",ans-dinic());
    return 0;
}

 

　　6.奶牛的电信：https://www.luogu.org/problemnew/show/P1345

　　题意概述：求一张图上至少坏掉多少点才能使得ST不连通。

　　和上一道题相仿，拆点。因为这次边不能断，所以原图中的边在新图中权值设为inf。

　　

# include <cstdio>
# include <iostream>
# include <cstring>
# include <queue>
# define inf 70000000

inline int min (int a,int b) { if(a<b) return a; return b; }
const int maxn=105;
const int maxm=605;
int n,m,s,t,x,y,h=1;
int firs[maxn<<1],d[maxn<<1];
bool vis[maxn<<1];
std::queue <int> q;
struct edge
{
    int too,nex,flow,cap;
}g[(maxm<<3)+maxn];

void add (int x,int y,int cap)
{
    g[++h].cap=cap;
    g[h].too=y;
    g[h].nex=firs[x];
    firs[x]=h;
}

bool bfs()
{
    std::memset(vis,0,sizeof(vis));
    while (q.size()) q.pop();
    q.push(s);
    vis[s]=true;
    d[s]=0;
    int beg,j;
    while (q.size())
    {
        beg=q.front();
        q.pop();
        for (int i=firs[beg];i;i=g[i].nex)
        {
            j=g[i].too;
            if(vis[j]) continue;
            if(g[i].cap<=g[i].flow) continue;
            d[j]=d[beg]+1;
            vis[j]=true;
            q.push(j);
        }
    }
    return vis[t];
}

int dfs (int x,int minf)
{
    if(minf==0||x==t) return minf;
    int j,flow=0,f;
    for (int i=firs[x];i;i=g[i].nex)
    {
        j=g[i].too;
        if(d[j]!=d[x]+1) continue;
        f=dfs(j,min(minf,g[i].cap-g[i].flow));
        if(f<=0) continue;
        g[i].flow+=f;
        g[i^1].flow-=f;
        minf-=f;
        flow+=f;
        if(minf==0) break;
    }
    return flow;
}

int maxflow()
{
    int ans=0;
    while (bfs())
        ans+=dfs(s,inf);
    return ans;
}

int main()
{
    scanf("%d%d%d%d",&n,&m,&s,&t);
    for (int i=1;i<=m;++i)
    {
        scanf("%d%d",&x,&y);
        add(x+n,y,inf);
        add(y,x+n,0);
        add(y+n,x,inf);
        add(x,y+n,0);
    }
    for (int i=1;i<=n;++i)
        if(i!=s&&i!=t)
        {
            add(i,i+n,1);
            add(i+n,i,0);
        }
    add(s,s+n,inf);
    add(s+n,s,0);
    add(t,t+n,inf);
    add(t+n,t,0);
    printf("%d",maxflow());
    return 0;
}

  

　　7.假期的宿舍：https://www.lydsy.com/JudgeOnline/problem.php?id=1433

　　题意概述：二分图最大匹配。

　　设立源点S，汇点T，S向一部连边，另一部向T连边，对于可以匹配的关系，就从S一侧向T一侧连边。注意：显然本校生可以睡自己的床。

　　

# include <cstdio>
# include <iostream>
# include <queue>
# include <cstring>
# define R register int
# define inf 1e8

int T;
int n,l,r,x,h,s=0,t;
int a[550],firs[550],d[550];
std::queue <int> q;
bool vis[150];
struct hu
{
    int nex,too,cap,flow;
}g[25009];

int min(int a,int b)
{
    if(a<b) return a;
    return b;
}

int dfs(int x,int minf)
{
    if(x==t||minf==0) return minf;
    int j,flow=0,f;
    for (R i=firs[x];i;i=g[i].nex)
    {
        j=g[i].too;
        if(d[j]!=d[x]+1) continue;
        f=dfs(j,min(minf,g[i].cap-g[i].flow));
        if(f<=0) continue;
        g[i].flow+=f;
        g[i^1].flow-=f;
        flow+=f;
        minf-=f;
        if(minf==0) break;
    }
    return flow;
}

bool bfs()
{
    memset(vis,0,sizeof(vis));
    vis[s]=true;
    while (q.size()) q.pop();
    q.push(s);
    int j,beg;
    while (q.size())
    {
        beg=q.front();
        q.pop();
        for (R i=firs[beg];i;i=g[i].nex)
        {
            j=g[i].too;
            if(vis[j]) continue;
            if(g[i].cap<=g[i].flow) continue;
            vis[j]=true;
            d[j]=d[beg]+1;
            q.push(j); 
        }
    }
    return vis[t];
}

int maxflow(int s)
{
    int ans=0;
    while (bfs())
        ans+=dfs(s,inf);
    return ans;
}

void add(int x,int y,int v)
{
    g[++h].too=y;
    g[h].nex=firs[x];
    firs[x]=h;
    g[h].cap=v;
    g[h].flow=0;
}

int main()
{
    scanf("%d",&T);
    while (T--)
    {
        h=1;
        l=0,r=0;
        memset(firs,0,sizeof(firs));
        scanf("%d",&n);
        for (int i=1;i<=n;++i)
        {
            scanf("%d",&a[i]);
            if(a[i]==0) a[i]=-1;
        }
        for (int i=1;i<=n;++i)
        {
            scanf("%d",&x);
            if(a[i]==1) a[i]-=x; //0:回家; 1:留下 
        }
        t=n*2+5;
        for (int i=1;i<=n;++i)
            if(a[i]!=0) l++,add(s,i,1),add(i,s,0);
        for (int i=1;i<=n;++i)
            if(a[i]>=0) add(i+n,t,1),add(t,i+n,0);
        for (int i=1;i<=n;++i)
            for (int j=1;j<=n;++j)
            {
                scanf("%d",&x);
                if(x||i==j)
                {
                    //i，j可以互相睡对方的床                     
                    if(a[i]>=0&&a[j]!=0)
                        add(j,i+n,1),add(i+n,j,0);
                    if(a[j]>=0&&a[i]!=0)
                        add(i,j+n,1),add(j+n,i,0);
                }
            }
        if(maxflow(s)<l) printf("T_T\n");
        else printf("^_^\n");    
    }
    return 0;
}

　　

　　8.分配问题：https://www.luogu.org/problemnew/show/P4014

　　题意概述：二分图最大带权匹配。

　　匹配关系上加上费用，跑费用流即可。

　　

# include <cstdio>
# include <iostream>
# include <cstring>
# include <queue>
# define R register int
# define inf 100000000

using namespace std;

const int maxn=102;
int ans,ans1,ans2,n,h=1,a[maxn][maxn],firs[maxn<<1],d[maxn<<1],pre[maxn<<1];
int in_que[maxn<<1],Fl[maxn<<1],s,t;
struct edge
{
    int too,nex,cap,co;
}g[maxn*maxn<<1];
queue <int> q;

void add (int x,int y,int cap,int co)
{
    g[++h].too=y;
    g[h].nex=firs[x];
    firs[x]=h;
    g[h].cap=cap;
    g[h].co=co;
    g[++h].too=x;
    g[h].nex=firs[y];
    firs[y]=h;
    g[h].cap=0;
    g[h].co=-co;
}

bool bfs (int col)
{
    if(col) memset(d,-0x3f,sizeof(d));
    else memset(d,0x3f,sizeof(d));
    q.push(s);
    int f=d[s];
    d[s]=0;
    Fl[s]=inf;
    int beg,j;
    while(q.size())
    {
        beg=q.front();
        q.pop();
        in_que[beg]=0;
        for (R i=firs[beg];i;i=g[i].nex)
        {
            j=g[i].too;
            if(g[i].cap<=0) continue;
            if(col&&d[j]>=d[beg]+g[i].co) continue;
            if(col==0&&d[j]<=d[beg]+g[i].co) continue;
            d[j]=d[beg]+g[i].co;
            pre[j]=i;
            Fl[j]=min(Fl[beg],g[i].cap);
            if(!in_que[j]) in_que[j]=true,q.push(j);
        }
    }
    return (d[t]!=f);
}

void dfs ()
{
    int x=t,i;
    while(x!=s)
    {
        i=pre[x];
        g[i].cap-=Fl[t];
        g[i^1].cap+=Fl[t];
        x=g[i^1].too;
    }
    ans+=d[t]*Fl[t];
}

int main()
{
    scanf("%d",&n);
    for (R i=1;i<=n;++i)
        for (R j=1;j<=n;++j)
            scanf("%d",&a[i][j]);
    t=2*n+1;
    for (R i=1;i<=n;++i)
        add(s,i,1,0),add(i+n,t,1,0);
    for (R i=1;i<=n;++i)
        for (R j=1;j<=n;++j)
            add(i,n+j,1,a[i][j]);
    while(bfs(0)) dfs();
    ans1=ans;
    ans=0;
    t=2*n+1;
    h=1,memset(firs,0,sizeof(firs));
    for (R i=1;i<=n;++i)
        add(s,i,1,0),add(i+n,t,1,0);
    for (R i=1;i<=n;++i)
        for (R j=1;j<=n;++j)
            add(i,n+j,1,a[i][j]);
    while(bfs(1)) dfs();
    ans2=ans;
    printf("%d\n%d",ans1,ans2);
    return 0;
}

 

　　9.试题库问题：https://www.luogu.org/problemnew/show/P2763

　　题意概述：题库中有很多的题目，每道题有多个属性，要求抽出M道题，每道题仅表现一种属性，使得表现每种属性的试题数量恰好为给定值。

　　这道题的题面有一点难理解，关键是要明白每道题一旦被选中，就只能表现一种属性，而不是所有属性都表现。

　　对于每种属性设置一个点，从源点向它连边，容量为需求量。对于每道题的每种属性，由属性向题目连边，容量为一。因为每道题只能贡献一种属性，所以由题目再向汇点连边。求一遍最大流，输出方案时找到每个属性连向的题目输出即可。

　　

# include <cstdio>
# include <iostream>
# include <cstring>
# include <queue>
# define R register int
# define inf 1000000009

using namespace std;

const int maxn=1050;
int n,k,m,firs[maxn],cur[maxn],d[maxn],h=1,s,t,S,x,y;
struct edge { int too,nex,cap,flow; } g[50004];
queue <int> q;

void add (int x,int y,int cap)
{
    g[++h].nex=firs[x];
    g[h].too=y;
    firs[x]=h;
    g[h].cap=cap;
    g[++h].nex=firs[y];
    g[h].too=x;
    firs[y]=h;
    g[h].cap=0;
}

bool bfs()
{
    memset(d,0,sizeof(d));
    d[s]=1;
    q.push(s);
    int beg,j;
    while(q.size())
    {
        beg=q.front();
        q.pop();
        for (R i=firs[beg];i;i=g[i].nex)
        {
            j=g[i].too;
            if(d[j]) continue;
            if(g[i].cap<=g[i].flow) continue;
            d[j]=d[beg]+1;
            q.push(j);
        }
    }
    return d[t];
}

int dfs (int x,int minf)
{
    if(minf==0||x==t) return minf;
    int flow=0,f,j;
    for (int& i=cur[x];i;i=g[i].nex)
    {
        j=g[i].too;
        if(d[j]!=d[x]+1) continue;
        f=dfs(j,min(minf,g[i].cap-g[i].flow));
        if(f<=0) continue;
        g[i].flow+=f;
        g[i^1].flow-=f;
        flow+=f;
        minf-=f;
        if(minf==0) break;
    }
    return flow;
}

void init() { for (R i=0;i<=t;++i) cur[i]=firs[i]; }

int dinic()
{
    int ans=0;
    while(bfs())
    {
        init();
        ans+=dfs(s,inf);
    }
    return ans;
}

int main()
{
    scanf("%d%d",&k,&n);
    t=k+n+1;
    for (R i=1;i<=k;++i)
        scanf("%d",&x),S+=x,add(s,i,x);
    for (R i=1;i<=n;++i)
    {
        add(i+k,t,1);
        scanf("%d",&x);
        for (R j=1;j<=x;++j)
        {
            scanf("%d",&y);
            add(y,i+k,1);
        }
    }
    if(dinic()!=S) puts("No Solution!");
    else
    {
        for (R i=1;i<=k;++i)
        {
            printf("%d:",i);
            for (R j=firs[i];j;j=g[j].nex)
            {
                if(j%2) continue;
                if(g[j].cap==g[j].flow) printf(" %d",g[j].too-k);
            }
            printf("\n");
        }
    }
    return 0;
}

　　

　　10.最小路径覆盖问题：https://www.luogu.org/problemnew/show/P2764

　　题意概述：DAG的最小点覆盖（找出最少的路径，使得每个点被经过恰好一次）。

　　如果直接按照题目的意思去做，就会非常麻烦，但是好像也不是不能做...就是每个点拆成出点和入点，中间连一条上下界均为一的边，每个入点和 S1 连边，出点和 T 连边，图中原有的边就按题意连一连，再从S向S'连边，对于这张图求一个带源汇上下界最小流即为答案。这样做的好处是非常好想“智商不够，高级算法来凑”。

　　简单一点的做法：首先要逆向思维，认为是每个点都独立成为路径，答案为N，再考虑哪些路径可以首尾相连变成一条。依旧拆点，对于原图中的每条边，由起点拆出的左点连向终点拆出的右点，形象化的理解就是某条路径到达它后没有结束，而是接着又连上了以终点为开头的一条新路径，做二分图最大匹配，即为“可以省掉的路径数目”。

　　

# include <cstdio>
# include <iostream>
# include <cstring>
# include <queue>
# define R register int
# define inf 1000000009

using namespace std;

const int maxn=302;
int ans,n,m,firs[maxn],s,t,h=1,x,y,vis[maxn],st[maxn],d[maxn],cur[maxn],r[maxn],Tp,f[maxn];
struct edge
{
    int too,nex,cap;
}g[20004];
queue <int> q;

inline int read()
{
    R x=0;
    char c=getchar();
    while (!isdigit(c)) c=getchar();
    while (isdigit(c)) x=(x<<3)+(x<<1)+(c^48),c=getchar();
    return x;
}

inline void add (int x,int y,int cap)
{
    g[++h].nex=firs[x];
    g[h].too=y;
    g[h].cap=cap;
    firs[x]=h;
    g[++h].nex=firs[y];
    g[h].too=x;
    g[h].cap=0;
    firs[y]=h;
}

int dfs (int x,int minf)
{
    if(x==t||minf==0) return minf;
    int j,f,flow=0;
    for (R &i=cur[x];i;i=g[i].nex)
    {
        j=g[i].too;
        if(d[j]!=d[x]+1) continue;
        f=dfs(j,min(minf,g[i].cap));
        if(f<=0) continue;
        g[i].cap-=f;
        g[i^1].cap+=f;
        flow+=f;
        minf-=f;
        if(minf==0) break;
    }
    return flow;
}

inline bool bfs ()
{
    int j,beg;
    memset(vis,0,sizeof(vis));
    d[s]=1;
    q.push(s);
    vis[s]=true;
    while (q.size())
    {
        beg=q.front();
        q.pop();
        for (R i=firs[beg];i;i=g[i].nex)
        {
            if(g[i].cap<=0) continue;
            j=g[i].too;
            if(vis[j]) continue;
            vis[j]=true;
            d[j]=d[beg]+1;
            q.push(j);
        }
    }
    return vis[t];
}

inline int dinic ()
{
    int ans=0;
    while (bfs())
    {
        for (R i=0;i<=t;++i) cur[i]=firs[i];
        ans+=dfs(s,inf);
    }
    return ans;
}

int main()
{
    n=read(),m=read();
    t=2*n+1;
    for (R i=1;i<=n;++i)
        add(s,i,1),add(i+n,t,1);
    for (R i=1;i<=m;++i)
    {
        x=read(),y=read();
        add(x,y+n,1);
    }
    ans=n-dinic();
    for (R i=1;i<=n;++i) f[i]=i;
    for (R i=1;i<=n;++i)
        for (R k=firs[i];k;k=g[k].nex)
        {
            if(k&1) continue;
            if(g[k].cap==0) 
            {
                f[ g[k].too-n ]=i;
                r[ i ]++;
                break;
            }
        }
    for (R i=1;i<=n;++i) if(!r[i]) q.push(i);
    int beg=0;
    while(q.size())
    {
        beg=q.front();
        q.pop();
        Tp=0;
        while (beg!=f[beg])
        {
            st[ ++Tp ]=beg;
            beg=f[beg];
        }
        st[++Tp]=beg;
        for (R i=Tp;i>=1;--i) printf("%d ",st[i]);
        printf("\n");
    }
    printf("%d",ans);
    return 0;
}

　　

　　11.无源汇上下界可行流：https://loj.ac/problem/115

　　循环往复，无始无终。

　　这个算法还是有一点难理解的，虽然上面讲过了，但是过于形式化，所以这里再写一些。

　　思路是先让所有的下界都满足，再用处于上下界之间的自由流来调整到合法。先将下界所需要的流都流上，并依此处理出每个点开始就有的流量，设为$a_i$。连边时流量设为 $max-min$，此时发现不满足流量平衡，而且网络流也没有什么“初始时就有的流”这么一说，所以让我们思考一下。如果一个点的初始流量大于0，也就是说对于仅保留自由流量边的那张新图，它的流出应该等于流入加 $a_i$ ,怎么实现这一要求呢？在网络流中，唯二可以不满足流量平衡的就是源和汇，所以可以加上一个附加源，向 $i$ 点连流量为$a_i$ 的边，附加汇同理。此时再跑一边最大流，如果所有的附加边都满流了，说明所有不合法的流都解决了，也就是一个可行流。

　　

# include <cstdio>
# include <iostream>
# include <string>
# include <cstring>
# include <queue>
# define R register int
# define inf 1000000009

using namespace std;

const int maxn=202;
int n,m,firs[maxn],h=1,a[maxn],d[maxn],s,t,x,y,mas,mis,flow[10405],cur[maxn],S;
struct edge { int too,nex,cap,flow; }g[25000];
queue <int> q;

inline int read()
{
    R x=0;
    char c=getchar();
    while (!isdigit(c)) c=getchar();
    while (isdigit(c)) x=(x<<3)+(x<<1)+(c^48),c=getchar();
    return x;
}

void add (int x,int y,int cap)
{
    g[++h].nex=firs[x];
    g[h].too=y;
    firs[x]=h;
    g[h].cap=cap;
    g[++h].nex=firs[y];
    g[h].too=x;
    firs[y]=h;
    g[h].cap=0;
}

bool bfs()
{
    memset(d,0,sizeof(d));
    d[s]=1;
    q.push(s);
    int beg,j;
    while(q.size())
    {
        beg=q.front();
        q.pop();
        for (R i=firs[beg];i;i=g[i].nex)
        {
            j=g[i].too;
            if(d[j]) continue;
            if(g[i].cap<=g[i].flow) continue;
            d[j]=d[beg]+1;
            q.push(j);
        }
    }
    return d[t];
}

int dfs (int x,int minf)
{
    if(minf==0||x==t) return minf;
    int flow=0,f,j;
    for (int& i=cur[x];i;i=g[i].nex)
    {
        j=g[i].too;
        if(d[j]!=d[x]+1) continue;
        f=dfs(j,min(minf,g[i].cap-g[i].flow));
        if(f<=0) continue;
        g[i].flow+=f;
        g[i^1].flow-=f;
        flow+=f;
        minf-=f;
        if(minf==0) break;
    }
    return flow;
}

void init() { for (R i=0;i<=t;++i) cur[i]=firs[i]; }

int dinic()
{
    int ans=0;
    while(bfs())
    {
        init();
        ans+=dfs(s,inf);
    }
    return ans;
}

int main()
{
    n=read(),m=read();
    t=n+1;
    for (R i=1;i<=m;++i)
    {
        x=read(),y=read(),mis=read(),mas=read();
        flow[i]=mis;
        add(x,y,mas-mis);
        a[y]+=mis,a[x]-=mis;
    }
    for (R i=1;i<=n;++i)
        if(a[i]>0) add(s,i,a[i]),S+=a[i];
        else add(i,t,-a[i]);
    if(dinic()!=S) puts("NO");
    else
    {
        puts("YES");
        for (R i=1;i<=m;++i)
            printf("%d\n",flow[i]+g[i*2].flow);
    }    
    return 0;
}

 

　　---shzr