【模板】容斥原理
集合形式
设 \(S\) 是一个有限集,\(A_1,A_2,\dots,A_n\) 是 \(S\) 的 \(n\) 个子集,则:
\(|S-\cup_{i=1}^{n}A_i|=\sum\limits_{i=0}^{n}(-1)^i\sum\limits_{1\le j_1\le j_2\le\dots\le j_i}|S\cap(\cap_{k=1}^iA_{j_k})|\)
符号形式
设 \(S\) 是一个有限集,\(a_1,a_2\dots a_n\) 是 \(n\) 中性质。
记 \(N(a_i)\) 为 \(S\) 中有 \(a_i\) 性质的元素的数量,特殊地,记 \(N(1)=|S|\)。
\(N(a_{j_1}a_{j_2}\dots a_{j_k})\) 为 \(S\) 中同时有 \(a_{j_1},a_{j_2},\dots,a_{j_k}\) 性质的元素的数量。
记 \(N(a+b)=N(a)+N(b),N(a-b)=N(a)-N(b)\)。
符号形式的优点
符号形式把容斥原理表达为代数形式。
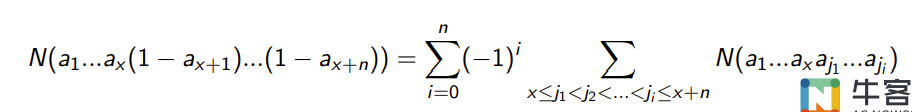
典型例题(必会)
- 求不定方程 \(x_1+x_2+\dots+x_k=n\) 的接的数量,其中 \(x_i\) 为非负整数,且 \(l_i\le x_i\le r_i(1\le i \le k)\)。
- \(p\) 是 \(1,2,\dots,n\) 的一个排列,满足刚好存在 \(k\) 个 \(1 \le i \le n\) 满足 \(p_i = i\),给定 \(n,k\),求满足要求的排列有多少个。
第二类斯特林数
定义
将 \(n\) 个两两不同的元素,划分为 \(k\) 个互不区分的非空子集的方案数,记作 \(S(n,k)\)。
递推式
\(S(n,k)=S(n-1,k-1)+kS(n-1,k)\)。
通项公式
\(S(n,m)=\sum\limits_{i=0}^{m}\frac{(-1)^{m-i}i^n}{i!(m-i)!}\)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号