2023.11.09
T1
题面

解题
-
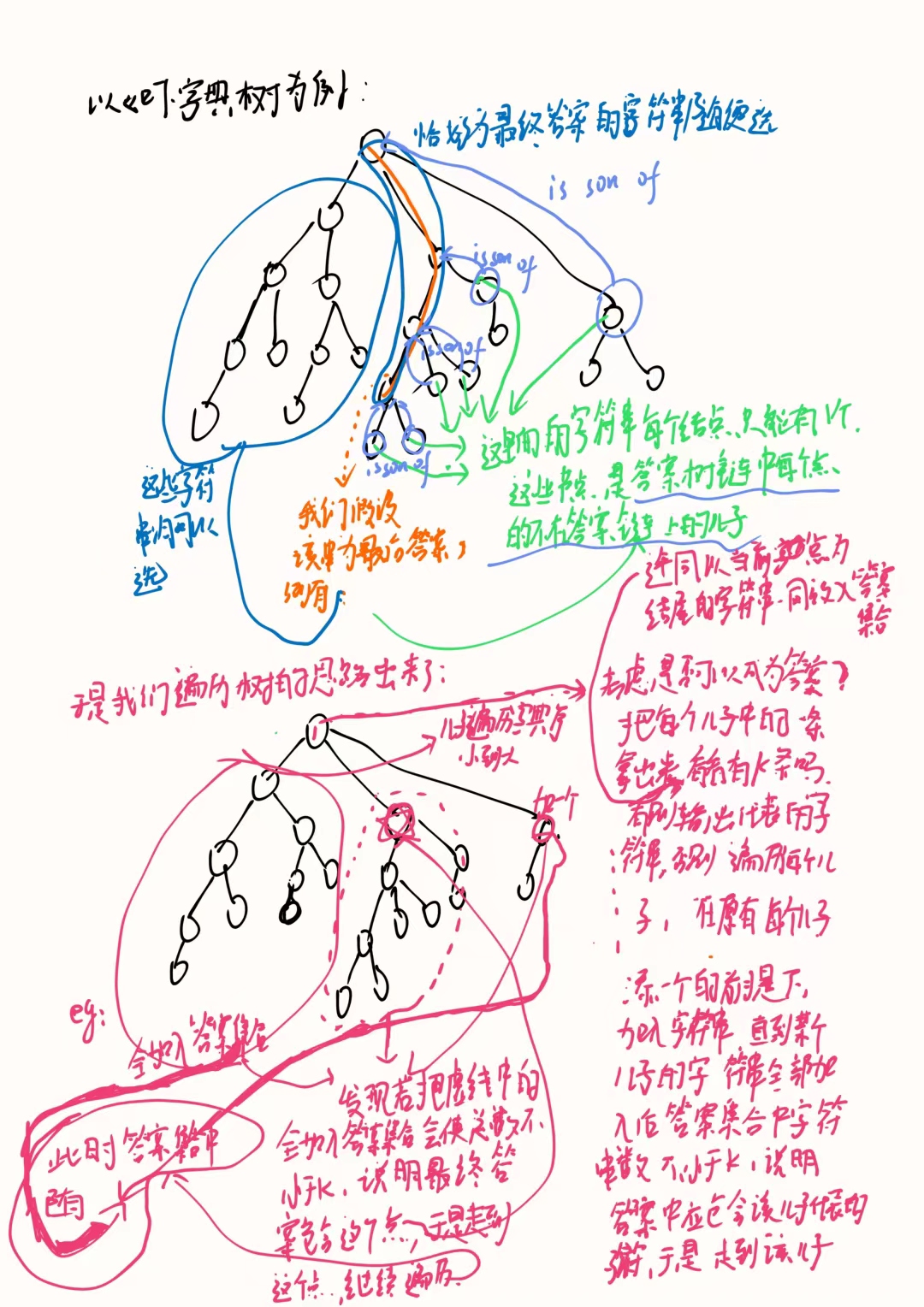
与字典序有关,考虑字典树。
-
考虑如何获得答案。贪心,判断以当前节点为结尾的字符串是否为答案,如果不是则继续遍历到当前节点的某个儿子。具体方式见下图。
-
时间复杂度为 \(\mathcal O(\sum|w|)\)。
代码
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int maxw=1e6+10;
int nxt[maxw][26],cnt,sz[maxw],tot[maxw];
int n,k,rt;
char s[maxw];
void build()
{
int now=rt,len=strlen(s+1);
tot[now]++;
for(int i=1;i<=len;i++)
{
int c=s[i]-'a';
if(!nxt[now][c]) nxt[now][c]=++cnt;
tot[now=nxt[now][c]]++;
}
sz[now]++;
}
void solve()
{
scanf("%d%d",&n,&k);
rt=++cnt;
for(int i=1;i<=n;i++)
{
scanf("%s",s+1);
build();
}
int now=rt;
while(true)
{
int t=sz[now];
for(int i=0;i<26;i++)
if(tot[nxt[now][i]]) t++;
if(t>=k)
{
if(now==rt) printf("EMPTY");
printf("\n");
return;
}
for(int i=0;i<26;i++)
{
if(tot[nxt[now][i]]==0) continue;
t+=-1+tot[nxt[now][i]];
if(t>=k)
{
k-=(t-tot[nxt[now][i]]);
printf("%c",'a'+i);
now=nxt[now][i];break;
}
}
}
}
int main()
{
int t;scanf("%d",&t);
while(t--) solve();
return 0;
}
T2
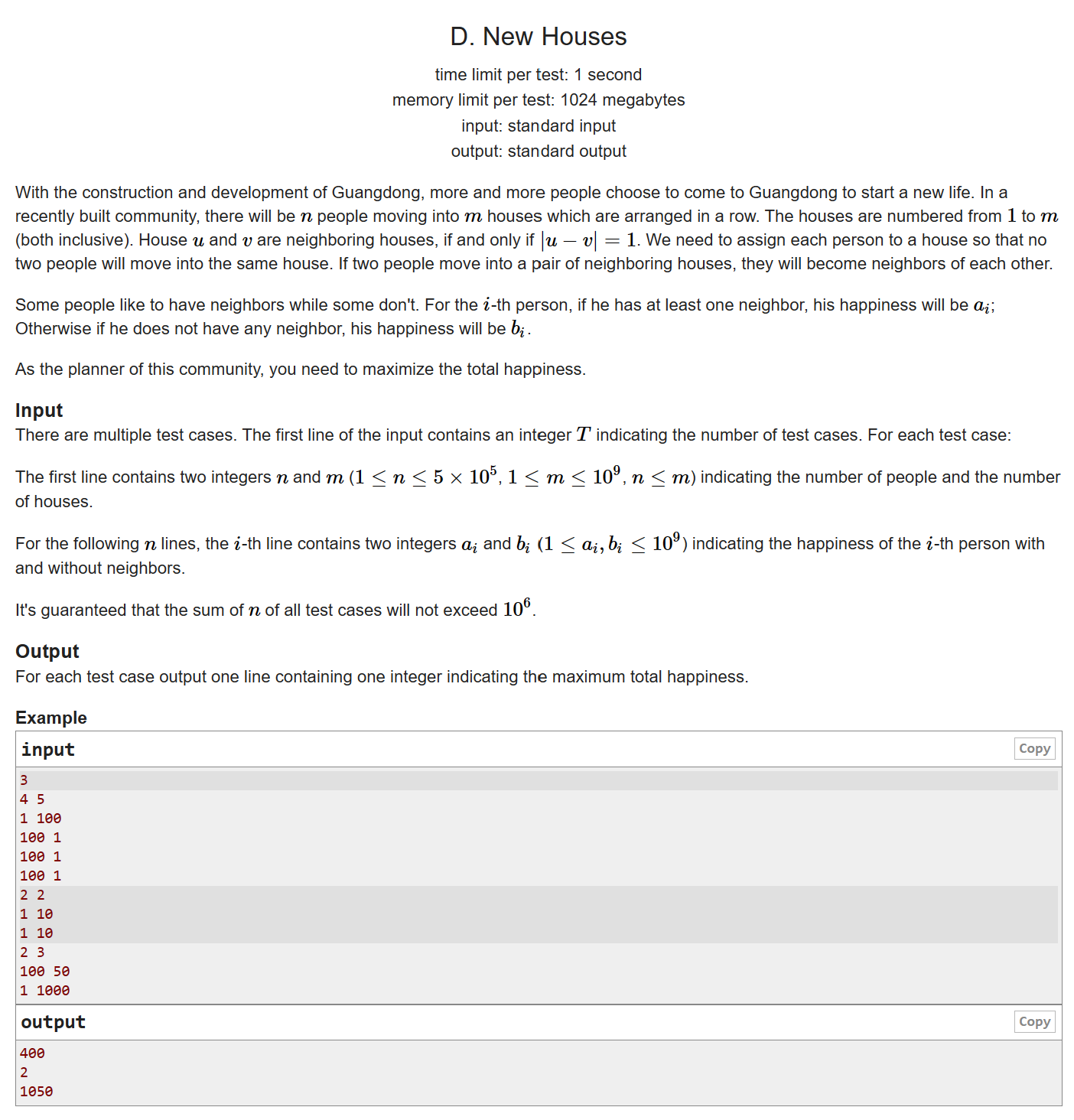
题面
解题
- 根据题意,所有人均需要安排住房。故每个人的贡献不是 \(a\) 便是 \(b\),而且相邻的人可以直接不管顺序地排在一起(因为不影响答案)。
- 故按 \(b-a\) 对人进行排序,倒序枚举断点 \(i\),断点以前的人排在一起;断点以后的人隔一个房子。易发现,断点越小,所占房子序列长度越大,故若无法长度大于 \(m\) 则终止遍历。同时发现,当 \(i==2\) 时,相当于所有人隔开,故 \(i\) 的下界为 \(3\);所有人隔开的情况单独讨论。
- 发现当 \(n==1\) 时,上述思路不成立(因为不可能有邻居,上述方法建立在可以有邻居的基础上),故需要特判。
- 时间复杂度为 \(\mathcal O(n\log n)\)。
代码
点击查看代码
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=5e5+100;
int n,m;
struct node
{
int a,b;
}e[maxn];
bool cmp(node a,node b)
{
return (a.b-a.a)<(b.b-b.a);
}
ll sumb[maxn],suma[maxn];
void solve()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%d%d",&e[i].a,&e[i].b);
if(n==1)
{
int maxa=0;
for(int i=1;i<=n;i++)
maxa=max(e[i].b,maxa);
printf("%d\n",maxa);
return;
}
sort(e+1,e+n+1,cmp);
for(int i=1;i<=n;i++)
suma[i]=suma[i-1]+e[i].a,
sumb[i]=sumb[i-1]+e[i].b;
/*
for(int i=1;i<=n;i++)
cout<<e[i].a<<" "<<e[i].b<<" "<<e[i].b-e[i].a<<"here\n";
*/
ll ans=suma[n];
for(int i=n;i>=3;i--)
{
if(i-1+2*(n-i+1)>m) break;
ans=max(ans,suma[i-1]+sumb[n]-sumb[i-1]);
}
if(2*n-1<=m) ans=max(ans,sumb[n]);
printf("%lld\n",ans);
}
int main()
{
int t;
scanf("%d",&t);
while(t--) solve();
return 0;
}
T3
题面

解题 1
- 贪心,买最便宜的,卖给价最高的,用双指针实现。
- 时间复杂度为 \(\mathcal O(n\log n)\)。
代码 1
点击查看代码
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=1e5+10;
int n;
struct node
{
int a,b;
} e[maxn];
bool cmp(node a,node b)
{
return a.a<b.a;
}
//ll sum[maxn],sumi[maxn];
void solve()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d%d",&e[i].a,&e[i].b);
sort(e+1,e+n+1,cmp);
ll ans=0;
int l=1,r=n;
while(l<r)
{
int num=min(e[l].b,e[r].b);
ans+=1ll*num*(e[r].a-e[l].a);
e[l].b-=num;e[r].b-=num;
if(!e[l].b) l++;
if(!e[r].b) r--;
}
printf("%lld\n",ans);
}
int main()
{
int t;scanf("%d",&t);
while(t--) solve();
return 0;
}
解题 2
- 贪心,按价格由小到达排序,再利用二分找到最小的非负的售出物件数与买入物件数之差所对应的状态,最后再把多余的不存在的售出从答案中扣掉即可。
- 两个错误调了一小时。第一个错误,寻找 idx 时将 \(l\) 的最小值设为 \(1\),本质是忽略了第一个次数大于后面所有次数之和的可能性。第二个错误,误以为一定存在买入物件数等于售出物件数的状态,实则不然。
代码 2
点击查看代码
#include<bits/stdc++.h>
#define ll long long
#define int long long
using namespace std;
const int maxn=1e5+10;
int n;
struct node
{
int a,b;
} e[maxn];
bool cmp(node a,node b)
{
return a.a<b.a;
}
ll sum[maxn],sumi[maxn];
void solve()
{
//cout<<1;
scanf("%lld",&n);
for(int i=1;i<=n;i++)
scanf("%lld%lld",&e[i].a,&e[i].b);
sort(e+1,e+n+1,cmp);
for(int i=1;i<=n;i++)
{
sum[i]=sum[i-1]+1ll*e[i].b;
sumi[i]=sumi[i-1]+1ll*e[i].a*e[i].b;
}
int l=0,r=n,idx=-1;
while(l<=r)
{
int mid=(l+r)>>1;
if(sum[mid]<=sum[n]-sum[mid])
idx=mid,l=mid+1;
else r=mid-1;
}
l=0,r=e[idx+1].b;int num=-1;
while(l<=r)
{
int mid=(l+r)>>1;
if(sum[idx]+mid<=sum[n]-sum[idx]-mid)
num=mid,l=mid+1;
else r=mid-1;
}
ll ans;
//cout<<sum[idx]<<" "<<sum[n]-sum[idx]<<endl;
ll tot=sum[n]-sum[idx]-num-(sum[idx]+num);
ans=sumi[n]-sumi[idx+1]+1ll*e[idx+1].a*(e[idx+1].b-num-tot);
ans-=sumi[idx]+1ll*e[idx+1].a*num;
printf("%lld\n",ans);
}
signed main()
{ //freopen("in.txt", "r", stdin); //?????????????
//freopen("Cwrong.txt", "w", stdout);
int t;scanf("%lld",&t);
while(t--) solve();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号