T1
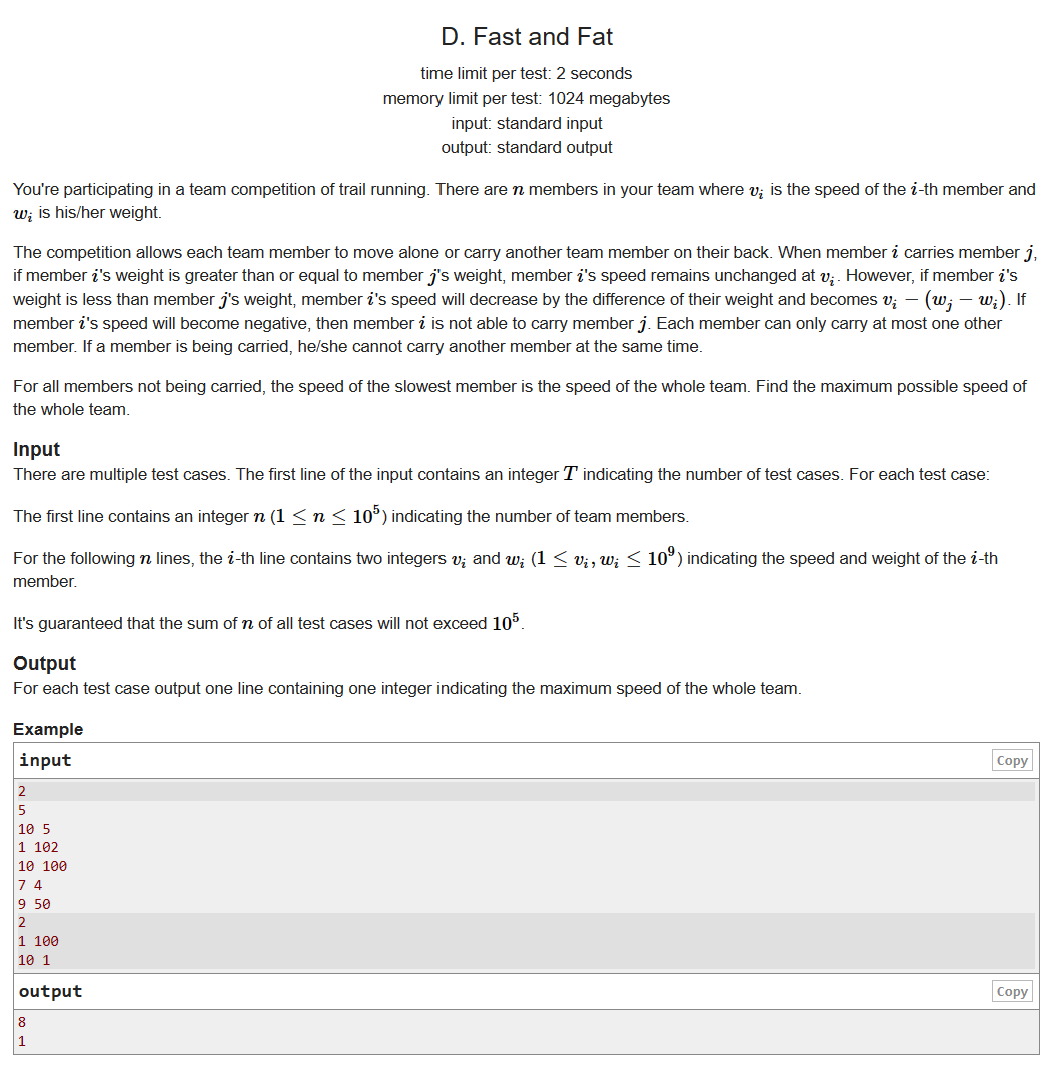
题面
解题
- 发现整个队伍的速度可以二分。若整个队伍的速度可以达到 \(x_0\),则对任意小于 \(x_0\) 的速度均可被满足;若整个队伍的速度不可以达到 \(x_0\),则任意大于 \(x_0\) 的速度均无法达到(若不然,整个队伍的速度可以满足 \(x_0\))。
- 考虑如何检验速度 \(x_0\) 是否可以达到。将所有成员分为两堆:速度大于等于 \(x_0\) 的成员(可以用来带人)与速度小于 \(x_0\) 的成员(需要被待)。故可以达到的标志为所有需要被带的成员均可被带。贪心,用带人能力强的成员去带难带的成员,判断是否需要被带的成员是否均可被带。
- 时间复杂度为 \(\mathcal O(n\log(\max\{v\}))\)。
代码
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
int a[maxn],n,w[maxn];
priority_queue<int,vector<int>,less<int>> q,qi,em;
bool check(int x)
{
q=em,qi=em;
for(int i=1;i<=n;i++)
if(a[i]>=x) q.push(a[i]+w[i]-x);
else qi.push(w[i]);
while(!qi.empty())
{
if(q.empty()) return false;
if(q.top()<qi.top()) return false;
q.pop(),qi.pop();
}
return true;
}
void solve()
{
scanf("%d",&n);
int ans=0,l=0,r=0;
for(int i=1;i<=n;i++)
scanf("%d%d",&a[i],&w[i]),r=max(r,a[i]);
while(l<=r)
{
int mid=(l+r)>>1;
if(check(mid)) ans=mid,l=mid+1;
else r=mid-1;
}
printf("%d\n",ans);
}
int main()
{
int t;scanf("%d",&t);
while(t--) solve();
return 0;
}
T2
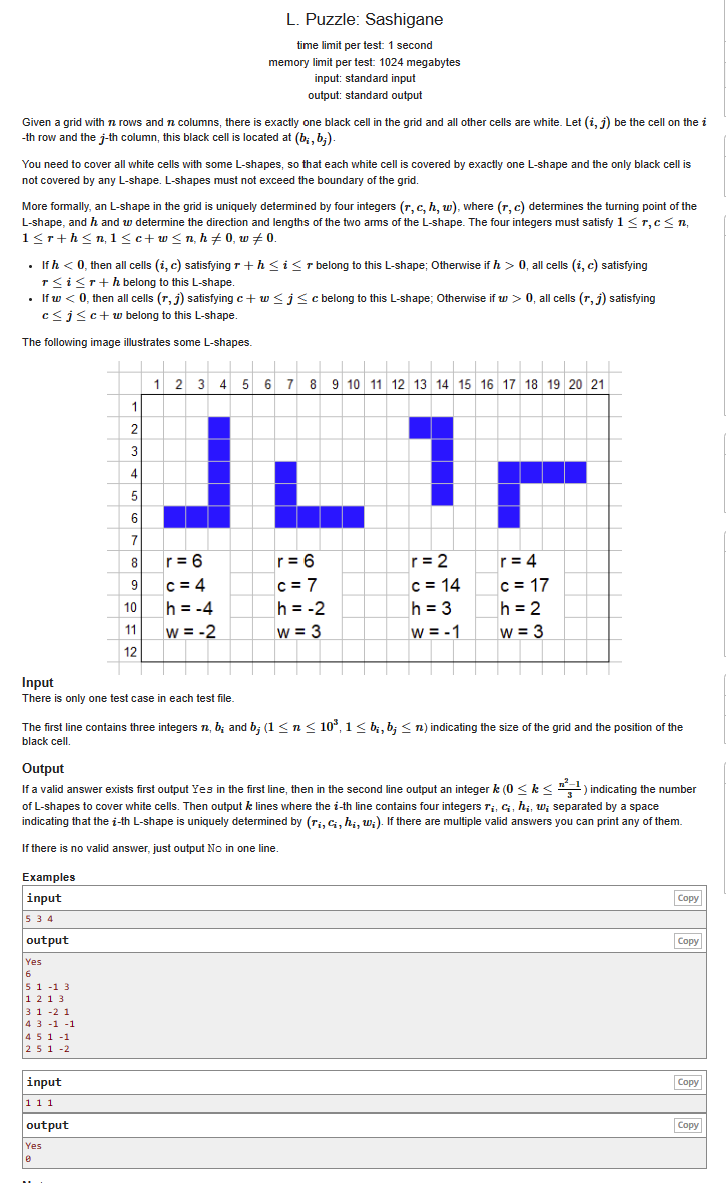
题面
解题
- 构造题。先以黑方块为中心,向外做正方形拓展(两个 L 叠起来),直到遇见边界 I。发现正方形与垂直于 I 的两个边界的距离之和恒等于正方形到与 I 平行的边界的距离,故恒可被构造。
- 时间复杂度为 \(\mathcal O(n)\)。
代码
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e3+10;
int n,bx,by;
bool check(int l,int r,int u,int d)
{
if(l<=1||l>=n) return false;
if(r<=1||r>=n) return false;
if(u<=1||u>=n) return false;
if(d<=1||d>=n) return false;
return true;
}
struct node
{
int r,c,h,w;
void print()
{
printf("%d %d %d %d\n",r,c,h,w);
}
};
void solve()
{
printf("Yes\n");
scanf("%d%d%d",&n,&bx,&by);
int l=by,r=by,u=bx,d=bx;
vector<node> ans;
while(check(l,r,u,d))
{
l--,r++,d++,u--;
int ri,ci,hi,wi;
int rii,cii,hii,wii;
ri=d,ci=r,hi=u-d+1,wi=l-r;
rii=u,cii=l,hii=d-u-1,wii=r-l;
ans.push_back((node){ri,ci,hi,wi});
ans.push_back((node){rii,cii,hii,wii});
}
//cout<<u<<" "<<d<<" "<<l<<" "<<r<<endl;
if(u==1)
{
int k=1;
for(int i=l-1;i>0;i--,k++)
{
int ri,ci,hi,wi;
ci=i,ri=d+k;
hi=1-d-k,wi=r-i;
ans.push_back((node){ri,ci,hi,wi});
}
for(int i=r+1;i<=n;i++,k++)
{
int ri,ci,hi,wi;
ci=i,ri=d+k;
hi=1-d-k,wi=1-i;
ans.push_back((node){ri,ci,hi,wi});
}
}
else if(l==1)
{
int k=1;
for(int i=u-1;i>0;i--,k++)
{
int ri,ci,hi,wi;
ri=i,ci=r+k;
hi=d-ri,wi=1-r-k;
ans.push_back((node){ri,ci,hi,wi});
}
for(int i=d+1;i<=n;i++,k++)
{
int ri,ci,hi,wi;
ri=i,ci=r+k;
hi=1-ri,wi=1-r-k;
ans.push_back((node){ri,ci,hi,wi});
}
}
else if(d==n)
{
int k=1;
for(int i=l-1;i>0;i--,k++)
{
int ri,ci,hi,wi;
ci=i,ri=u-k;
hi=n-ri,wi=r-i;
ans.push_back((node){ri,ci,hi,wi});
}
for(int i=r+1;i<=n;i++,k++)
{
int ri,ci,hi,wi;
ci=i,ri=u-k;
hi=n-ri,wi=1-i;
ans.push_back((node){ri,ci,hi,wi});
}
}
else if(r==n)
{
int k=1;
for(int i=u-1;i>0;i--,k++)
{
int ri,ci,hi,wi;
ri=i,ci=l-k;
hi=d-ri,wi=n-ci;
ans.push_back((node){ri,ci,hi,wi});
}
for(int i=d+1;i<=n;i++,k++)
{
int ri,ci,hi,wi;
ri=i,ci=l-k;
hi=1-ri,wi=n-ci;
ans.push_back((node){ri,ci,hi,wi});
}
}
printf("%d\n",ans.size());
vector<node>::iterator it;
for(it=ans.begin();it!=ans.end();it++)
{
node ansi=*it;
ansi.print();
}
}
int main()
{
int t=1;//scanf("%d",&t);
while(t--) solve();
return 0;
}
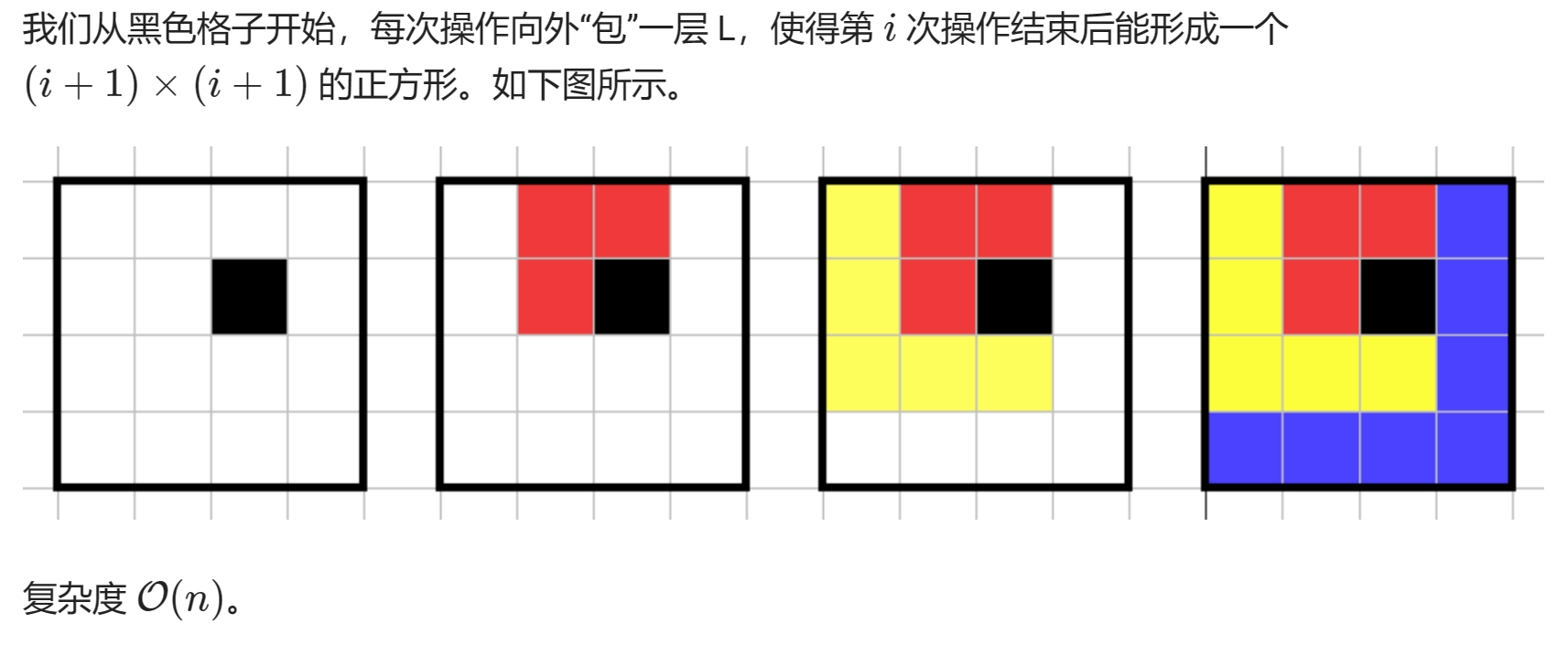
正解思路
正解代码
点击查看代码
#include <bits/stdc++.h>
using namespace std;
int main() {
int n, i, j; scanf("%d%d%d", &n, &i, &j);
// UDLR 表示现在包出来的正方形的上下左右边界
int U = i, D = i;
int L = j, R = j;
printf("Yes\n%d\n", n - 1);
for (int k = 1; k < n; k++) {
if (U > 1 && L > 1) {
U--; L--;
printf("%d %d %d %d\n", U, L, D - U, R - L);
} else if (U > 1 && R < n) {
U--; R++;
printf("%d %d %d %d\n", U, R, D - U, L - R);
} else if (D < n && L > 1) {
D++; L--;
printf("%d %d %d %d\n", D, L, U - D, R - L);
} else {
D++; R++;
printf("%d %d %d %d\n", D, R, U - D, L - R);
}
}
return 0;
}





 浙公网安备 33010602011771号
浙公网安备 33010602011771号