T1
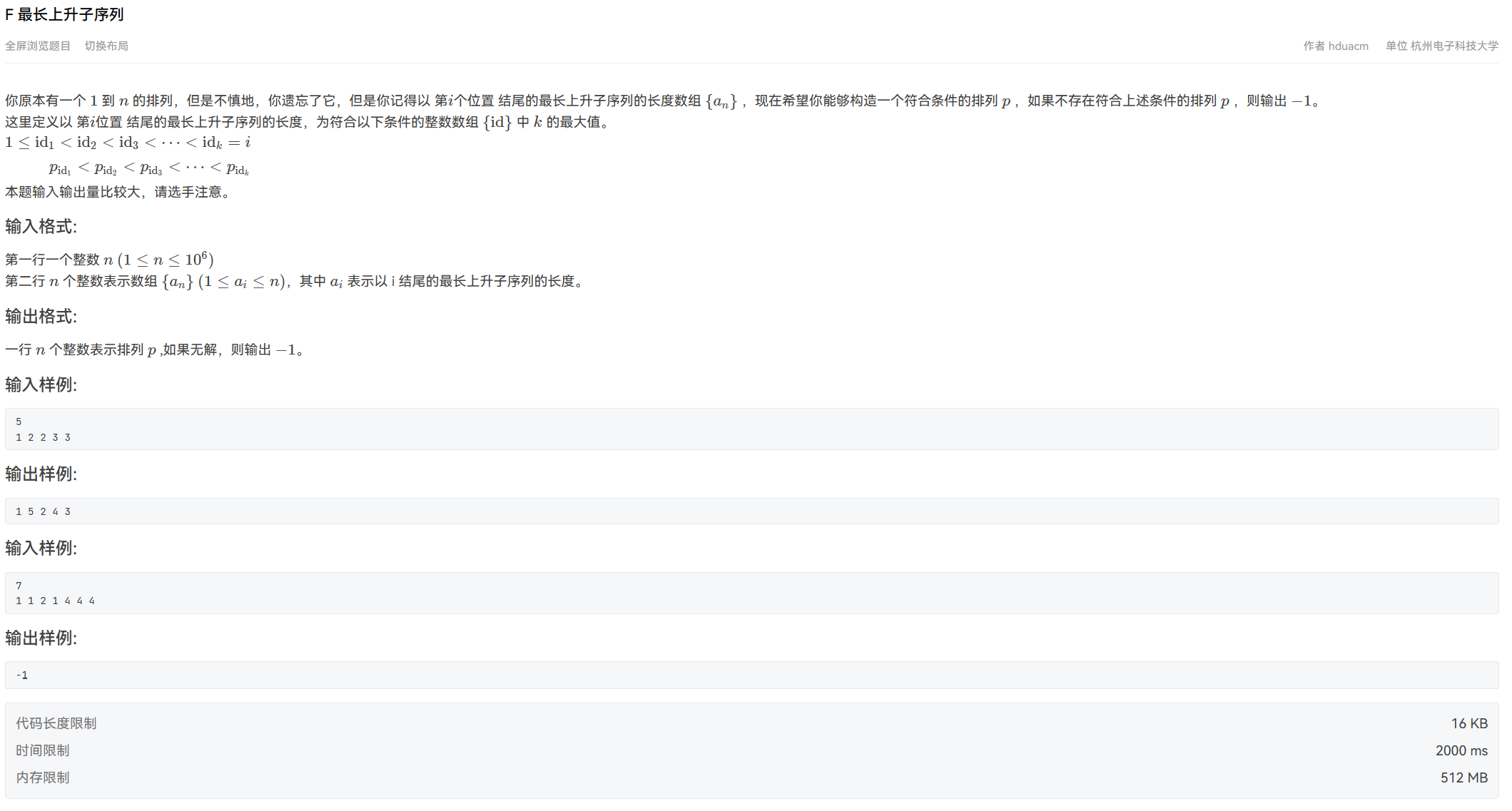
题面
解题
- 首先考虑何时无法构造。根据递推式 \(dp_i=\max\limits_{j<i且h_j<h_i}\{dp_j\}+1\) 可知:该题中的 \(a\) 序列若存在 \(a_{i_0}=k\),则一定存在 \(i_1<i_0\),使得\(a_{i_1}=k-1\);否则,排列无法被构造,输出 \(-1\)。
- 考虑满足条件的排列如何被构造出来。取极端例子 \(a_i=1,\forall i\),易得此时满足题意的排列为 \(n,n-1,\dots,1\)。在该基础上,考虑序列 \(a\) 为 \(\{1,1,\dots,1,2,\dots,2\}\) 的情形,设 \(cnt\) 为 \(a\) 中 \(1\) 的数目,则易得,\(cnt,cnr-1,\dots,1,n,n-1,\dots,cnt+1\) 满足条件。
- 故一般化的构造方式为,统计 \(i\) 在 \(a\) 中出现的次数 \(cnt_i\),将 \((\sum\limits_{j<i}cnt_j)+1\) 到 \((\sum\limits_{j\le i}cnt_j)\) 的整数“分配”给 \(i\),并在 \(a\) 序列遇见 \(i\) 时输出还未使用的分配给 \(i\) 的数的最大值。正确性容易验证。
- 时间复杂度为 \(\mathcal O(n)\)。
代码
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+5;
int n,a[maxn],num[maxn],idx[maxn];
int sum[maxn];
int main()
{
scanf("%d",&n);
num[0]=1;
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
idx[i]=++num[a[i]];
if(num[a[i]-1]==0){printf("-1");return 0;}
}
for(int i=1;i<=n;i++)
sum[i]=sum[i-1]+num[i];
for(int i=1;i<=n;i++)
printf("%d ",sum[a[i]]-idx[i]+1);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号