Ch2——数据分析之numpy模块的应用

Numpy模块的应用

1、数组（创建和操作）

（1）创建：

将列表或元组通过array()函数转化为数组；如，

import numpy as np

arr1 = np.array([[1, 10, 100],		 # 列表转数组
                 [2, 20, 200],
                 [3, 30, 300]])
# 或者如下法
arr = np.array(list)        # 列表转化为数组，数组转列表用tolist

注：数组元素的返回

1）在一维数组中，列表的所有索引方法都可以使用在数组中，而且还可以将任意位置的索引组装为列表，用作对应元素的获取；

2）在二维数组中，位置索引必须写成[rows,cols]的形式，方括号的前半部分用于锁定二维数组的行索引，后半部分用于锁定数组的列索引；

3）如果需要获取二维数组的所有行或列元素，那么，对应的行索引或列索引需要用英文状态的冒号表示；

如下测试：

import numpy as np

# 一维数组
arr1 = np.array([3,10,8,7,34,11,28,72])
# 一维数组元素的获取
print(arr1[[2,3,5,7]])				# 1）
 
# 二维数组元素的获取
# 第2行第3列元素
print(arr2[1,2])					# 2）
# 第3行所有元素
print(arr2[2,:])					# 2），3）
# 第2列所有元素
print(arr2[:,1])					# 2），3）
# 第2至4行，2至5列
print(arr2[1:4,1:5])				# 2），3）

输出结果： （pycharm输出）

[ 8  7 11 72]

5.4

[ 3.2  3.   3.8  3.   3. ]

[  6.    3.    3.   13.4]

[[  3.    5.4   7.3   9. ]
 [  3.    3.8   3.    3. ]
 [ 13.4  15.6  17.8  19. ]]

（2）操作：

①数组常用的属性：

ndim：返回数组的维数（返回1，表示1维数组；返回2，表示二维数组）

shape：返回数组的行列数（返回结果为元组结构）

dtype：返回数组元素的数据类型

size：返回数组元素的个数

如下测试：

import numpy as np

arr = np.array([[1, 10, 100],
                [2, 20, 200],
                [3, 30, 300]])
# 查看数据结构
print(type(arr))
# 查看数据维数
print(arr.ndim)
# 查看数据行列数
print(arr.shape)
# 查看数组元素的数据类型
print(arr.dtype)
# 查看数组元素个数
print(arr.size)

输出结果： （pycharm输出）

<class 'numpy.ndarray'>
2
(3, 3)
int32
9

②数组形状的处理:

1）常用的属性

flatten：与ravel功能类似

reshape：用于转换数组的形状，如原本3×4的数组转换成6×2的数组

resize：与reshape功能类似，区别在于reshape无法原地修改数组的形状，而resize可以

ravel：将多维数组转换为一维数组的方法

测试1：（reshape和resize）

import numpy as np

# 创建数组
arr3 = np.array([[1,5,7],[3,6,1],[2,4,8],[5,8,9],[1,5,9],[8,5,2]])
# 数组的行列数
print(arr3.shape)
# 使用reshape方法更改数组的形状
print(arr3.reshape(2,9))
# 打印数组arr3的行列数
print(arr3.shape)

# 使用resize方法更改数组的形状，该方法无返回值
print(arr3.resize(2,9))
# 打印数组arr3的行列数
print(arr3.shape)

输出结果： （pycharm输出）

(6, 3)
[[1 5 7 3 6 1 2 4 8]
 [5 8 9 1 5 9 8 5 2]]
(6, 3)
None
(2, 9)

小结：

reshape方法只是返回改变形状后的预览，并未真的改变数组形状；resize方法则不会返回预览，而直接更改；

.

测试2：（flatten，reshape和ravel）

import numpy as np

# 构造3×3的二维矩阵
arr4 = np.array([[1,10,100],[2,20,200],[3,30,300]])
print('原数组：\n',arr4)
# 默认排序降维（默认按行的顺序降维）
print('数组降维：\n',arr4.ravel())
print(arr4.flatten())
print(arr4.reshape(-1))
# 改变排序模式的降维（按列的顺序降维）
print(arr4.ravel(order = 'F'))
print(arr4.flatten(order = 'F'))
print(arr4.reshape(-1, order = 'F'))

输出结果：（pycharm输出）

原数组：
 [[  1  10 100]
 [  2  20 200]
 [  3  30 300]]

数组降维：
[  1  10 100   2  20 200   3  30 300]
[  1  10 100   2  20 200   3  30 300]
[  1  10 100   2  20 200   3  30 300]
[  1   2   3  10  20  30 100 200 300]
[  1   2   3  10  20  30 100 200 300]
[  1   2   3  10  20  30 100 200 300]

小结：

• 在默认情况下，优先按照数组的行顺序，逐个将元素降至一维（参见数组降维的前三行打印结果）；
• 如果按原始数组的列顺序，将数组降为一维的话，需要设置 order参数为“F”（参见数组降维的后三行打印结果）。

.

测试3：（flatten，reshape和ravel）

# 测试flatten，ravel和reshape
"""
小结：
①flatten降维后，返回的是复制品，改变不了原数组；
②ravel()和reshape(-1)会将数组先实行降维(即搞成一维的)返回值为视图，再只需根据列号去改变数组的值；
"""
import numpy as np

arr1 = np.array([[1, 10, 100],
                 [2, 20, 200],
                 [3, 30, 300]])

print('………………………………flatten………………………………')
arr1.flatten()[3] = 2000
print(arr1)

print('………………………………ravel………………………………')
arr1.ravel()[3] = 1000       # ravel会把数组展平（即搞成一维的），只需要改变列就行，故只有一个'[]';
print(arr1)

print('………………………………reshape………………………………')
arr1.reshape(-1)[3] = 3000   # reshape同ravel；
print(arr1)

输出结果：（pycharm输出）

………………………………flatten………………………………
[[  1  10 100]
 [  2  20 200]
 [  3  30 300]]
………………………………ravel………………………………
[[   1   10  100]
 [1000   20  200]
 [   3   30  300]]
………………………………reshape………………………………
[[   1   10  100]
 [3000   20  200]
 [   3   30  300]]
 

小结：

• flatten降维后，返回的是复制品，改变不了原数组；
• ravel()和reshape(-1)会将数组先实行降维(即搞成一维的)返回值为视图，再只需根据列号去改变数组的值；

③数组的堆叠和合并：

1）常用的属性

row_stack：用于垂直方向（纵向）的数组堆叠

vstack：用于垂直方向（纵向）的数组堆叠

colum_stack：用于水平方向（横向）的数组合并

hstack：用于水平方向（横向）的数组合并

测试：

# 测试vstack和row_stack,以及hstack和column_stack
"""
小结：
①vstack([a, b])和row_stack([a,b])为纵向堆叠，即就是把b数组堆到a数组的底下；(注：必须保证a，b列数相同，可多个数组进行)
②hstack([a,b])和column_stack([a,b])为横向合并，即就是把b数组加到a数组的右侧；(注：必须保证a，b行数相同，可多个数组进行)
"""
import numpy as np 

arr1 = np.array([[1, 10, 100],
                 [2, 20, 200],
                 [3, 30, 300]])

arr2 = [1, 2, 3]
print('……………………纵向堆叠数组……………………')             # 说白了就是谁在后面写着，就放到前一个底下
print('vstack:\n', np.vstack([arr1, arr2]))
print('row_stack:\n', np.row_stack([arr1, arr2]))

arr3 = [[5], [15], [25]]
print('……………………横向合并数组……………………')             # 同理，谁在后面写着，就加在前一个的右侧
print('hstack:\n', np.hstack([arr1, arr3]))
print('column_stack:\n', np.column_stack([arr1, arr3]))

输出结果：（pycharm输出）

……………………纵向堆叠数组……………………
vstack:
 [[  1  10 100]
 [  2  20 200]
 [  3  30 300]
 [  1   2   3]]
row_stack:
 [[  1  10 100]
 [  2  20 200]
 [  3  30 300]
 [  1   2   3]]
……………………横向合并数组……………………
hstack:
 [[  1  10 100   5]
 [  2  20 200  15]
 [  3  30 300  25]]
column_stack:
 [[  1  10 100   5]
 [  2  20 200  15]
 [  3  30 300  25]]
 

小结：

• vstack([a, b])和row_stack([a,b])为纵向堆叠，即就是把b数组堆到a数组的底下；(注：必须保证a，b列数相同，可多个数组进行)
• hstack([a,b])和column_stack([a,b])为横向合并，即就是把b数组加到a数组的右侧；(注：必须保证a，b行数相同，可多个数组进行)

2、数组（基本运算）

（1）数组的基本运算方法

1）数学运算符

运算符	含义	运算符	含义
+	数组对应元素的加和	-	数组对应元素的差
*****	数组对应元素的乘积	/	数组对应元素的商
%	数组对应元素商的余数	//	数组对应元素商的整除数
******	数组对应元素的幂指数

2）比较运算符

符号	函数	含义
>	np.greater(arr1,arr2)	判断arr1的元素是否大于arr2的元素
>=	np.greater_equal(arr1,arr2)	判断arr1的元素是否大于等于arr2的元素
<	np.less(arr1,arr2)	判断arr1的元素是否小于arr2的元素
<=	np.less_equal(arr1,arr2)	判断arr1的元素是否小于等于arr2的元素
==	np.equal(arr1,arr2)	判断arr1的元素是否等于arr2的元素
!=	np.not_equal(arr1,arr2)	判断arr1的元素是否不等于arr2的元素

（2）常用的数学和统计函数

1）常用的数学函数

函数	函数说明
np.pi	常数Π【派】
np.e	常数e
np.fabs(arr)	计算各元素的浮点型绝对值
np.ceil(arr)	对各元素向上取整
np.floor(arr)	对各元素向下取整
np.round(arr)	对各元素四舍五入
np.fmod(arr1,arr2)	计算arr1/arr2的余数
np.modf(arr)	返回数组元素的小数部分和整数部分
np.sqrt(arr)	计算各元素的算术平方根
np.square(arr)	计算各元素的平方值
np.exp(arr)	计算以e为底的指数
np.power(arr, α)	计算各元素的指数
np.log2(arr)	计算以2为底各元素的对数
np.log10(arr)	计算以10为底各元素的对数
np.log(arr)	计算以e为底各元素的对数

2）常用的统计函数

函数	函数说明
np.min(arr,axis)	按照轴的方向计算最小值
np.max(arr,axis)	按照轴的方向计算最大值
np.mean(arr,axis)	按照轴的方向计算平均值
np.median(arr,axis)	按照轴的方向计算中位数
np.sum(arr,axis)	按照轴的方向计算和（axis：0为垂直；1为水平）
np.std(arr,axis)	按照轴的方向计算标准差
np.var(arr,axis)	按照轴的方向计算方差
np.cumsum(arr,axis)	按照轴的方向计算累计和
np.cumprod(arr,axis)	按照轴的方向计算累计乘积
np.argmin(arr,axis)	按照轴的方向返回最小值所在的位置
np.argmax(arr,axis)	按照轴的方向返回最大值所在的位置
np.corrcoef(arr)	计算皮尔逊相关系数
np.cov(arr)	计算协方差矩阵

3）常用的线代函数

函数	说明	函数	说明
np.zeros	生成零矩阵	np.ones	生成所有元素为1的矩阵
np.eye	生成单位矩阵	np.transpose	矩阵转置
np.dot	计算两个数组的点积	np.inner	计算两个数组的内积
np.diag	矩阵主对角线与一维数组间的转换	np.trace	矩阵主对角线元素的和
np.linalg.det	计算矩阵行列式	np.linalg.eig	计算矩阵特征根与特征向量
np.linalg.eigvals	计算方阵特征根	np.linalg.inv	计算方阵的逆
np.linalg.pinv	计算方阵的Moore-Penrose伪逆	np.linalg.solve	计算Ax=b的线性方程组的解
np.linalg.lstsq	计算Ax=b的最小二乘解	np.linalg.qr	计算QR分解
np.linalg.svd	计算奇异值分解	np.linalg.norm	计算向量或矩阵的范数

范例1：

# 计算方阵的特征向量和特征根
import numpy as np

arr = np.array([[1, 2, 5],
                [3, 6, 8],
                [4, 7, 9]])
print('计算3×3方阵的特征根和特征向量：\n', arr)
print('求解结果为：\n', np.linalg.eig(arr))

输出结果：（pycharm输出）

计算3×3方阵的特征根和特征向量：
 [[1 2 5]
 [3 6 8]
 [4 7 9]]
求解结果为：
 (
 array([16.75112093, -1.12317544,  0.37205451]), 
 array([[-0.30758888, -0.90292521,  0.76324346],
       [-0.62178217, -0.09138877, -0.62723398],
       [-0.72026108,  0.41996923,  0.15503853]])
       )
       

范例2：

\[三元方程： 3x+2y+z=39; 2x+3y+z=34; x+2y+3z=26 \]

# 多元线性方程组
import numpy as np

A = np.array([[3, 2, 1],
              [2, 3, 1],
              [1, 2, 3]])
b = np.array([39, 34, 26])
X = np.linalg.solve(A, b)
print('三元一次方程组的解：\n', X)

输出结果：（pycharm输出）

三元一次方程组的解：
 [9.25 4.25 2.75]
 

4）常用的随机分布函数（用于伪随机数的生成）

函数	说明
seed(n)	设置随机种子
beta(a, b, size=None)	生成贝塔分布随机数
chisquare(df, size=None)	生成卡方分布随机数
choice(a, size=None, replace=True, p=None)	从a中有放回地随机挑选指定数量的样本
exponential(scale=1.0, size=None)	生成指数分布随机数
f(dfnum,dfden, size=None)	生成F分布随机数
gamma(shape, scale=1.0, size=None)	生成伽马分布随机数
geometric(p, size=None)	生成几何分布随机数
hypergeometric(ngood, nbad, nsample, size=None)	生成超几何分布随机数
laplace(loc=0.0, scale=1.0, size=None)	生成拉普拉斯分布随机数
logistic(loc=0.0, scale=1.0, size=None)	生成Logistic分布随机数
lognormal(mean=0.0, sigma=1.0, size=None)	生成对数正态分布随机数
negative_binomial(n, p, size=None)	生成负二项分布随机数
multinomial(n, pvals, size=None)	生成多项分布随机数
multivariate_normal(mean, cov[, size])	生成多元正态分布随机数
normal(loc=0.0, scale=1.0, size=None)	生成正态分布随机数
pareto(a, size=None)	生成帕累托分布随机数
poisson(lam=1.0, size=None)	生成泊松分布随机数
rand(d0, d1, ..., dn)	生成n维的均匀分布随机数
randn(d0, d1, ..., dn)	生成n维的标准正态分布随机数
randint(low, high=None, size=None, dtype='l')	生成指定范围的随机整数
random_sample(size=None)	生成[0,1)的随机数
standard_t(df, size=None)	生成标准的t分布随机数
uniform(low=0.0, high=1.0, size=None)	生成指定范围的均匀分布随机数
wald(mean, scale, size=None)	生成Wald分布随机数
weibull(a, size=None)	生成Weibull分布随机数

范例1：

# 导入第三方模块
import seaborn as sns
import matplotlib.pyplot as plt
from scipy import stats

# 生成各种正态分布随机数
np.random.seed(1234)
rn1 = np.random.normal(loc=0, scale=1, size=1000)
rn2 = np.random.normal(loc=0, scale=2, size=1000)
rn3 = np.random.normal(loc=2, scale=3, size=1000)
rn4 = np.random.normal(loc=5, scale=3, size=1000)

# 绘图
plt.style.use('ggplot')
sns.distplot(rn1, hist=False, kde=False, fit=stats.norm,
             fit_kws={'color': 'black', 'label': 'u=0,s=1', 'linestyle': '-'})
sns.distplot(rn2, hist=False, kde=False, fit=stats.norm,
             fit_kws={'color': 'red', 'label': 'u=0,s=2', 'linestyle': '--'})
sns.distplot(rn3, hist=False, kde=False, fit=stats.norm,
             fit_kws={'color': 'blue', 'label': 'u=2,s=3', 'linestyle': ':'})
sns.distplot(rn4, hist=False, kde=False, fit=stats.norm,
             fit_kws={'color': 'purple', 'label': 'u=5,s=3', 'linestyle': '-.'})

# 呈现图例
plt.legend()
# 呈现图形
plt.show()

输出结果：（pycharm输出）

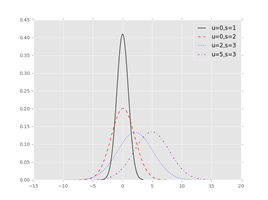
范例2：

import seaborn as sns
import matplotlib.pyplot as plt
from scipy import stats

# 生成各种指数分布随机数
np.random.seed(1234)
re1 = np.random.exponential(scale=0.5, size=1000)
re2 = np.random.exponential(scale=1, size=1000)
re3 = np.random.exponential(scale=1.5, size=1000)
# 绘图
sns.distplot(re1, hist=False, kde=False, fit=stats.expon,
             fit_kws={'color': 'black', 'label': 'lambda=0.5', 'linestyle': '-'})
sns.distplot(re2, hist=False, kde=False, fit=stats.expon,
             fit_kws={'color': 'red', 'label': 'lambda=1', 'linestyle': '--'})
sns.distplot(re3, hist=False, kde=False, fit=stats.expon,
             fit_kws={'color': 'blue', 'label': 'lambda=1.5', 'linestyle': ':'})
# 呈现图例
plt.legend()
# 呈现图形
plt.show()

输出结果：（pycharm输出）

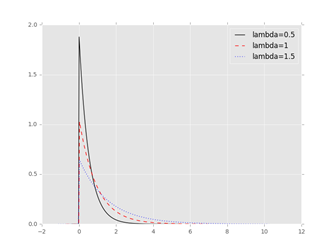
注：部分图片、数据来源网络侵删；