机械手臂-DH参数
机械手臂的一个重要特征参数就是DH参数。
具体资料可查询:维基百科英文版:http://en.wikipedia.org/wiki/Denavit%E2%80%93Hartenberg_parameters
由于被墙,现摘录如下:
Denavit–Hartenberg parameters
The Denavit–Hartenberg parameters (also called DH parameters) are the four parameters associated with a particular convention for attaching reference frames to the links of a spatial kinematic chain, or robot manipulator.
Jacques Denavit and Richard Hartenberg introduced this convention in 1955 in order to standardize the coordinate frames for spatial linkages. [1] [2]
Richard Paul demonstrated its value for the kinematic analysis of robotic systems in 1981.[3] While many conventions for attaching references frames have been developed, the Denavit-Hartenberg convention remains the standard approach.
Contents[hide] |
A commonly used convention for selecting frames of reference in robotics applications is the Denavit and Hartenberg (D–H) convention which was introduced by Jacques Denavit and Richard S. Hartenberg. In this convention, coordinate frames are attached to the joints between two links such that one transformation is associated with the joint, [Z], and the second is associated with the link [X]. The coordinate transformations along a serial robot consisting of n links form the kinematics equations of the robot,
where [T] is the transformation locating the end-link.
In order to determine the coordinate transformations [Z] and [X], the joints connecting the links are modeled as either hinged or sliding joints, each of which have a unique line S in space that forms the joint axis and define the relative movement of the two links. A typical serial robot is characterized by a sequence six lines Si, i=1,...,6, one for each joint in the robot. For each sequence of lines Si and Si+1, there is a common normal line Ai,i+1. The system of six joint axes Si and five common normal lines Ai,i+1 form the kinematic skeleton of the typical six degree of freedom serial robot. Denavit and Hartenberg introduced the convention that Z coordinate axes are assigned to the joint axes Si and X coordinate axes are assigned to the common normals Ai,i+1.
This convention allows the definition of the movement of links around a common joint axis Si by the screw displacement,
where θi is the rotation around and di is the slide along the Z axis---either of the parameters can be constants depending on the structure of the robot. Under this convention the dimensions of each link in the serial chain are defined by the screw displacement around the common normal Ai,i+1 from the joint Si to Si+1, which is given by
where αi,i+1 and ai,i+1 define the physical dimensions of the link in terms of the angle measured around and distance measured along the X axis.
In summary, the reference frames are laid out as follows:
- the
![z]() -axis is in the direction of the joint axis
-axis is in the direction of the joint axis - the
![x]() -axis is parallel to the common normal:
-axis is parallel to the common normal: ![x_n = z_n \times z_{n-1}]()
If there is no unique common normal (parallel![z]() axes), then
axes), then ![d]() (below) is a free parameter. The direction of
(below) is a free parameter. The direction of ![x_n]() is from
is from ![z_{n - 1}]() to
to ![z_n]() , as shown in the video below.
, as shown in the video below. - the
![y]() -axis follows from the
-axis follows from the ![x]() - and
- and ![z]() -axis by choosing it to be a right-handed coordinate system.
-axis by choosing it to be a right-handed coordinate system.
The transformation is then described by the following four parameters known as D–H parameters:.[4]
![d\,]() : offset along previous
: offset along previous ![z]() to the common normal
to the common normal![\theta\,]() : angle about previous
: angle about previous ![z]() , from old
, from old ![x]() to new
to new ![x]()
![r\,]() : length of the common normal (aka
: length of the common normal (aka ![a]() , but if using this notation, do not confuse with
, but if using this notation, do not confuse with ![\alpha]() ). Assuming a revolute joint, this is the radius about previous
). Assuming a revolute joint, this is the radius about previous ![z]() .
.![\alpha\,]() : angle about common normal, from old
: angle about common normal, from old ![z]() axis to new
axis to new ![z]() axis
axis
A visualization of D–H parameterization is available:
There is some choice in frame layout as to whether the previous  axis or the next
axis or the next  points along the common normal. The latter system allows branching chains more efficiently, as multiple frames can all point away from their common ancestor, but in the alternative layout the ancestor can only point toward one successor. Thus the commonly used notation places each down-chain
points along the common normal. The latter system allows branching chains more efficiently, as multiple frames can all point away from their common ancestor, but in the alternative layout the ancestor can only point toward one successor. Thus the commonly used notation places each down-chain  axis collinear with the common normal, yielding the transformation calculations shown below.
axis collinear with the common normal, yielding the transformation calculations shown below.
We can note constraints on the relationships between the axes:
- the
![x_n]() -axis is perpendicular to both the
-axis is perpendicular to both the ![z_{n - 1}]() and
and ![z_n]() axes
axes - the
![x_n]() -axis intersects both
-axis intersects both ![z_{n - 1}]() and
and ![z_n]() axes
axes - the origin of joint
![n]() is at the intersection of
is at the intersection of ![x_n]() and
and ![z_n]()
![y_n]() completes a right-handed reference frame based on
completes a right-handed reference frame based on ![x_n]() and
and ![z_n]()
It is common to separate a screw displacement into the product of a pure translation along a line and a pure rotation about the line,[5][6] so that
and
Using this notation, each link can be described by a coordinate transformation from the previous coordinate system to the next coordinate system.
Note that this is the product of two screw displacements, The matrices associated with these operations are:
This gives:
where R is the 3×3 submatrix describing rotation and T is the 3×1 submatrix describing translation.
The Denavit and Hartenberg notation gives a standard methodology to write the kinematic equations of a manipulator. This is specially useful for serial manipulators where a matrix is used to represent the pose (position and orientation) of one body with respect to another.
The position of body  with respect to
with respect to 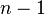 may be represented by a position matrix indicated with the symbol
may be represented by a position matrix indicated with the symbol  or
or 
This matrix is also used to transform a point from frame  to
to 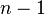
Where the upper left  submatrix of
submatrix of  represents the relative orientation of the two bodies, and the upper right
represents the relative orientation of the two bodies, and the upper right  represents their relative position.
represents their relative position.
The position of body  with respect to body
with respect to body  can be obtained as the product of the matrices representing the pose of
can be obtained as the product of the matrices representing the pose of  with respect of
with respect of  and that of
and that of  with respect of
with respect of 
An important property of Denavit and Hartenberg matrices is that the inverse is
where  is both the transpose and the inverse of the orthogonal matrix
is both the transpose and the inverse of the orthogonal matrix  , i.e.
, i.e. 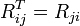 .
.
Kinematics
Further matrices can be defined to represents velocity and acceleration of bodies.[5][6] The velocity of body  with respect to body
with respect to body  can be represented in frame
can be represented in frame  by the matrix
by the matrix
where  is the angular velocity of body
is the angular velocity of body  with respect to body
with respect to body  and all the components are expressed in frame
and all the components are expressed in frame  ;
;  is the velocity of one point of body
is the velocity of one point of body  with respect to body
with respect to body  (the pole). The pole is the point of
(the pole). The pole is the point of  passing through the origin of frame
passing through the origin of frame  .
.
The acceleration matrix can be defined as the sum of the time derivative of the velocity plus the velocity squared
The velocity and the acceleration in frame  of a point of body
of a point of body  can be evaluated as
can be evaluated as
It is also possible to prove that
Velocity and acceleration matrices add up according to the following rules
in other words the absolute velocity is the sum of the drag plus the relative velocity; for the acceleration the Coriolis' term is also present.
The components of velocity and acceleration matrices are expressed in an arbitrary frame  and transform from one frame to another by the following rule
and transform from one frame to another by the following rule
[edit]Dynamics
For the dynamics 3 further matrices are necessary to describe the inertia  , the linear and angular momentum
, the linear and angular momentum  , and the forces and torques
, and the forces and torques 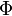 applied to a body.
applied to a body.
Inertia  :
:
where  is the mass,
is the mass, 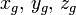 represent the position of the center of mass, and the terms
represent the position of the center of mass, and the terms  represent inertia and are defined as
represent inertia and are defined as
Action matrix 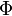 , containing force
, containing force  and torque
and torque  :
:
Momentum matrix  , containing linear
, containing linear  and angular
and angular  momentum
momentum
the all the matrices are represented with the vector components in a certain frame  . Transformation of the components from frame
. Transformation of the components from frame  to frame
to frame 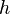 follows to rule
follows to rule
The matrices described allow the writing of the dynamic equations in a concise way.
Newton's law:
Momentum:
The first of these equations express the Newton's law and is the equivalent of the vector equation 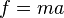 (force equal mass times acceleration) plus
(force equal mass times acceleration) plus  (angular acceleration in function of inertia and angular velocity); the second equation permits the evaluation of the linear and angular momentum when velocity and inertia are known.
(angular acceleration in function of inertia and angular velocity); the second equation permits the evaluation of the linear and angular momentum when velocity and inertia are known.
See also
- Forward kinematics
- Inverse kinematics
- Kinematic chain
- Kinematics
- Robotics conventions
- Mechanical systems
References
- ^ Denavit, Jacques; Hartenberg, Richard Scheunemann (1955). "A kinematic notation for lower-pair mechanisms based on matrices". Trans ASME J. Appl. Mech 23: 215–221.
- ^ Hartenberg, Richard Scheunemann; Denavit, Jacques (1965). Kinematic synthesis of linkages. McGraw-Hill series in mechanical engineering. New York: McGraw-Hill. p. 435.
- ^ Paul, Richard (1981). Robot manipulators: mathematics, programming, and control : the computer control of robot manipulators. Cambridge, MA: MIT Press. ISBN 978-0-262-16082-7.
- ^ Spong, Mark W.; Vidyasagar, M. (1989). Robot Dynamics and Control. New York: John Wiley & Sons. ISBN 9780471503521.
- ^ a b Legnani, G.; Casolo, F.; Righettini, P.; Zappa, B. (1996). "A homogeneous matrix approach to 3D kinematics and dynamics — I. Theory". Mechanism and Machine Theory 31 (5): 573. doi:10.1016/0094-114X(95)00100-D.
- ^ a b Legnani, G.; Casalo, F.; Righettini, P.; Zappa, B. (1996). "A homogeneous matrix approach to 3D kinematics and dynamics—II. Applications to chains of rigid bodies and serial manipulators". Mechanism and Machine Theory 31 (5): 589. doi:10.1016/0094-114X(95)00101-4.
一台6轴的机械手臂以马达旋转中心点抽象为6个点与连杆结构。


![[T] = [Z_1][X_1][Z_2][X_2]\ldots[X_{n-1}][Z_n],\!](http://upload.wikimedia.org/math/4/e/4/4e4c3130996237ba753fc369788a72e9.png)
![[Z_i]=\begin{bmatrix}\cos\theta_i & -\sin\theta_i & 0 & 0 \\ \sin\theta_i & \cos\theta_i & 0 & 0 \\ 0 & 0 & 1 & d_i \\ 0 & 0 & 0 & 1\end{bmatrix},](http://upload.wikimedia.org/math/6/e/a/6ea09816a24bb802a328c9d02e339250.png)
![[X_i]=\begin{bmatrix} 1 & 0 & 0 & a_{i,i+1} \\ 0 & \cos\alpha_{i,i+1} & -\sin\alpha_{i,i+1} & 0 \\ 0& \sin\alpha_{i,i+1} & \cos\alpha_{i,i+1} & 0 \\ 0 & 0 & 0 & 1\end{bmatrix},](http://upload.wikimedia.org/math/a/0/2/a029f63fb243c937cd9688b8e74110e1.png)
 -axis is in the direction of the joint axis
-axis is in the direction of the joint axis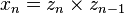
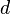 (below) is a free parameter. The direction of
(below) is a free parameter. The direction of  is from
is from  to
to  , as shown in the video below.
, as shown in the video below. -axis follows from the
-axis follows from the  : offset along previous
: offset along previous 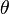 : angle about previous
: angle about previous  : length of the common normal (aka
: length of the common normal (aka  , but if using this notation, do not confuse with
, but if using this notation, do not confuse with  ). Assuming a revolute joint, this is the radius about previous
). Assuming a revolute joint, this is the radius about previous 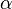 : angle about common normal, from old
: angle about common normal, from old  completes a right-handed reference frame based on
completes a right-handed reference frame based on ![[Z_i] = \operatorname{Trans}_{Z_{i}}(d_i) \operatorname{Rot}_{Z_{i}}(\theta_i),](http://upload.wikimedia.org/math/7/1/e/71e1de2513825968a73a31682e0c76d0.png)
![[X_i]=\operatorname{Trans}_{X_i}(a_{i,i+1})\operatorname{Rot}_{X_i}(\alpha_{i,i+1}).](http://upload.wikimedia.org/math/f/7/f/f7f05375ce05de37360dcad372a82a29.png)
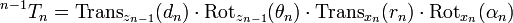
![\operatorname{Trans}_{z_{n - 1}}(d_n)
=
\left[
\begin{array}{ccc|c}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & d_n \\
\hline
0 & 0 & 0 & 1
\end{array}
\right]](http://upload.wikimedia.org/math/e/0/a/e0aac9d9f6780a1ff96eb01fdaf1fd90.png)
![\operatorname{Rot}_{z_{n - 1}}(\theta_n)
=
\left[
\begin{array}{ccc|c}
\cos\theta_n & -\sin\theta_n & 0 & 0 \\
\sin\theta_n & \cos\theta_n & 0 & 0 \\
0 & 0 & 1 & 0 \\
\hline
0 & 0 & 0 & 1
\end{array}
\right]](http://upload.wikimedia.org/math/d/6/4/d64d4260b225baa34fd360a22b1de597.png)
![\operatorname{Trans}_{x_n}(a_n)
=
\left[
\begin{array}{ccc|c}
1 & 0 & 0 & a_n \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
\hline
0 & 0 & 0 & 1
\end{array}
\right]](http://upload.wikimedia.org/math/3/3/e/33ed6bdbcc43613b43e6d059a9d6c1bc.png)
![\operatorname{Rot}_{x_n}(\alpha_n)
=
\left[
\begin{array}{ccc|c}
1 & 0 & 0 & 0 \\
0 & \cos\alpha_n & -\sin\alpha_n & 0 \\
0 & \sin\alpha_n & \cos\alpha_n & 0 \\
\hline
0 & 0 & 0 & 1
\end{array}
\right]](http://upload.wikimedia.org/math/3/4/e/34e2694b4bc75e066d7b6794d3e1635e.png)
![\operatorname{}^{n - 1}T_n
=
\left[
\begin{array}{ccc|c}
\cos\theta_n & -\sin\theta_n \cos\alpha_n & \sin\theta_n \sin\alpha_n & a_n \cos\theta_n \\
\sin\theta_n & \cos\theta_n \cos\alpha_n & -\cos\theta_n \sin\alpha_n & a_n \sin\theta_n \\
0 & \sin\alpha_n & \cos\alpha_n & d_n \\
\hline
0 & 0 & 0 & 1
\end{array}
\right]
=
\left[
\begin{array}{ccc|c}
& & & \\
& R & & T \\
& & & \\
\hline
0 & 0 & 0 & 1
\end{array}
\right]](http://upload.wikimedia.org/math/c/8/4/c849f51de6a7f042a0653b43cede0939.png)

![P_{(n-1)} = M_{n-1,n} P_{(n)} = \left[ \begin{array}{c} x_{n-1} \\y_{n-1} \\z_{n-1} \\ 1 \end{array} \right] = \left[ \begin{array}{ccc|c} X_x & Y_x & Z_x & T_x \\ X_y & Y_y & Z_y & T_y \\ X_z & Y_z & Z_z & T_z \\
\hline
0 & 0 & 0 & 1 \end{array}\right]
\left[ \begin{array}{c} x_{n} \\y_{n} \\z_{n} \\ 1 \end{array} \right]](http://upload.wikimedia.org/math/f/6/4/f645eb04a4944a47b3acb16801ce2e48.png)

![M^{-1} =
\left[
\begin{array}{ccc|c}
& & & \\
& R^T & & -R^T T \\
& & & \\
\hline
0 & 0 & 0 & 1
\end{array}
\right]](http://upload.wikimedia.org/math/6/a/4/6a4789404a71efb5c8738195bd16f14a.png)
![W_{i,j(k)}=\left[ \begin{array}{ccc|c} 0 & -\omega_z & \omega_y & v_x \\ \omega_z & 0 & -\omega_x & v_y \\ -\omega_y & \omega_x & 0 & v_z \\
\hline
0 & 0 & 0 & 0 \end{array}\right]](http://upload.wikimedia.org/math/4/3/e/43e1eec26ece2124e10be09dd7200200.png)

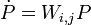
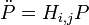
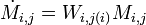
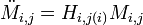
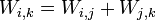
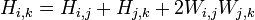


![J=\left[ \begin{array}{ccc|c} I_{xx} & I_{xy} & I_{xz} & x_g m \\ I_{xy} & I_{yy} &
I_{yz} & y_g m \\ I_{xz} & I_{yz} & I_{zz} & z_g m \\
\hline
x_g m & y_g m & z_g m & m \end{array}\right]](http://upload.wikimedia.org/math/d/6/f/d6facb50a809696d52ec2150774a1ab2.png)

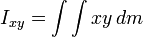

![\Phi = \left[ \begin{array}{ccc|c} 0 & -t_z & t_y & f_x \\ t_z & 0 & -t_x & f_y \\ -t_y & t_x & 0 & f_z \\
\hline
-f_x & -f_y & -f_z & 0 \end{array}\right]](http://upload.wikimedia.org/math/a/1/c/a1cc600838111e6d06dd7106da1c446b.png)
![\Phi = \left[ \begin{array}{ccc|c} 0 & -\gamma_z & \gamma_y & \rho_x \\ \gamma_z & 0 & -\gamma_x & \rho_y \\ -\gamma_y & \gamma_x & 0 & \rho_z \\
\hline
-\rho_x & -\rho_y & -\rho_z & 0 \end{array}\right]](http://upload.wikimedia.org/math/d/2/7/d2734e965c5246644b67d85be3e2e488.png)






 浙公网安备 33010602011771号
浙公网安备 33010602011771号