数据结构 图的定义及其四种存储结构（邻接矩阵法、邻接表法、十字链表法存储有向图、邻接多重表）

8、图

8.1、图的概念和定义

图G由顶点集V和边集E组成，记为G=(V,E)，其中V(G)表示图G中定点的有限非空集；E(G)表示图G中顶点之间的关系（边）的集合。若$V = \({\)V_1,V_2,V_3...V_n$}，则用==|V|==表示图G的==顶点个数==，也称==图G的阶==，$E=\({\)(u,v)|u属于V，v属于V$}，用|E|表示图G边的条数

注意：图不可以是空图

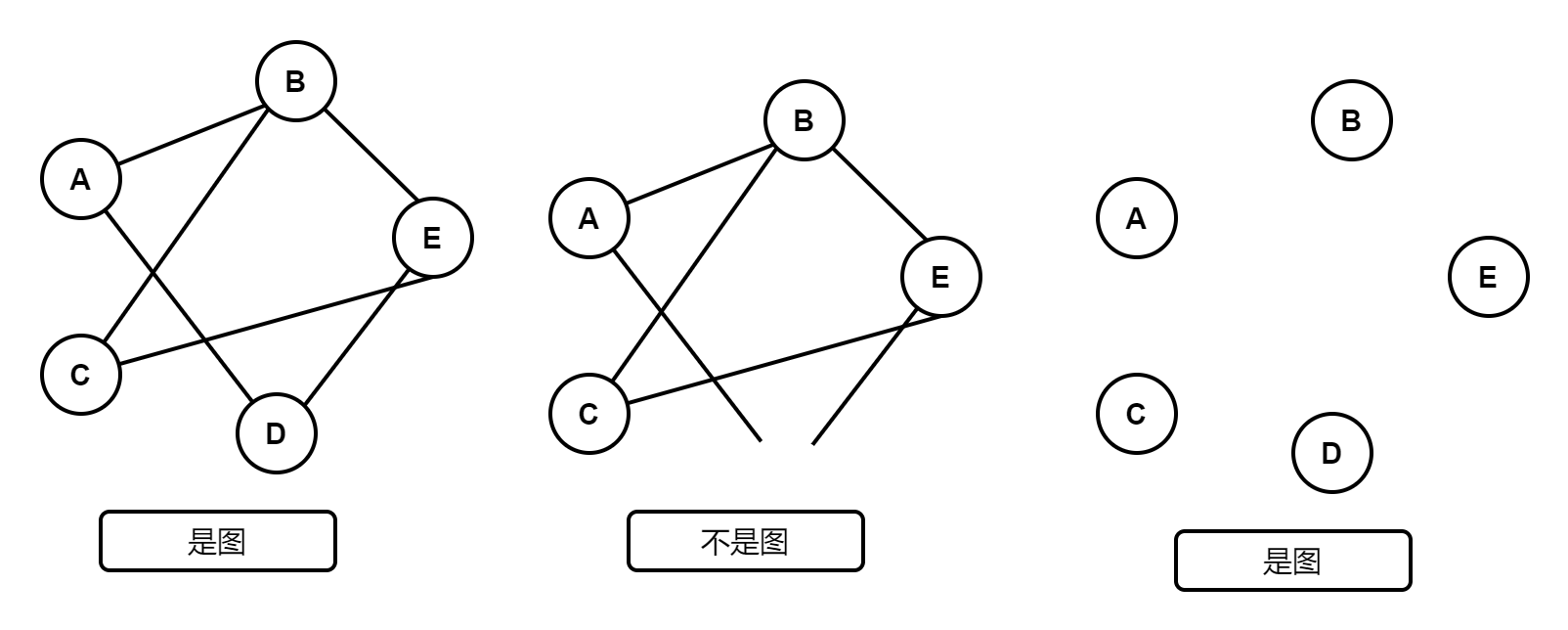
有向图、无向图

无向图

若E是无向边（简称边）的有限集合时，则图G是无向图，边是顶点的无序对，记为(w,v)或者(v,w)，因为(w,v)=(v,w)，其中w，v是顶点。可以说w，v互为邻接点。边(v,w)依附于顶点w和v，或者说边(w,v)和顶点w、v相关联。

有向图

若E是有向边（简称弧）的有限集合时，则图G是有向图。弧是顶点的有序对，记为<w,v>，其中w、v是顶点，w称为弧尾，v称为弧头，<w,v>称为从顶点w到顶点v的弧，也称w邻接到v，或者w邻接自v。<w,v>!=<v,w>

简单图、多重图

简单图 —— 不存在重复的边，不存在顶点到自身的边

多重图 —— 图G中某两个结点之间的边数多余一条，有允许顶点通过一条边和自己关联

顶点的度、入度、出度

对于无向图，顶点v的度指依附于该顶点的边的条数，记为TD(v)。

如边的顶点数n、数量为e：$\sum_{i=1}^{n}TD(v_i) = 2e$

对于有向图:

• 入度：是以顶点v为终点的有向边的数目，记为ID(v)
• 出度：是以顶点v为起点的有向边的数目，记为OD(v)
• TD(v) = OD(v) + ID(v)

如边的边数为n、数量为e：$\sum_{i=1}^{n}OD(v_i) = \sum_{i=1}^{n}ID(v_i) = e$

顶点与顶关系的描述

• 路径：顶点v到顶点w之间的一条路径是指顶点序列
• 回路：第一个顶点和最后一个顶点相同的路径称为回路或环
• 简单路径：在路径序列中，顶点不重复出现的路径称为简单路径
• 简单回路：除了第一个顶点和最后一个顶点外，其余顶点不重复出现的回路称为简单回路
• 路径长度：路径上边的数目
• 点到点的距离：从顶点u出发到顶点v的最短路径若存在，则次路径的长度称为u到v的距离，若u到v不存在路径，则距离为无穷
• 在无向图中，若顶点v到顶点w路径存在，则称v和w连通
• 在有向图中，若顶点v到顶点w和顶点w到顶点v之间都有路径，则称这两个顶点是强连通的

对于n个顶点的无向图G：

若G是连通图，则最少有n-1条边

若G是非连通图，则最多有$C_{n-1}^{2}$条边

对于n个顶点的有向图G：

若G是强连通图，则最少有n条边（形成回路）。

连通图的生成树：包含图中全部顶点的一个极小连通子图

边的权、带权图/网：

• 带权边：一个图中，在每条边都可以标上具有某种含义的数值，数值称为该边的权值
• 带权图/网：边上带有权值的图称为带权图，也称为网
• 带权路径长度：当图是带权图时，一条路径上所有边的权值之和，称为该路径的带权路径长度

无向完全图：无向图中任意两个顶点之间都存在边

有向完全图：有向图中任意两个顶点之间都存在方向相反的两条弧

8.2、邻接矩阵法

顶点数为n，使用n*n的矩阵来表示边的信息，1表示相连，0表示不相连

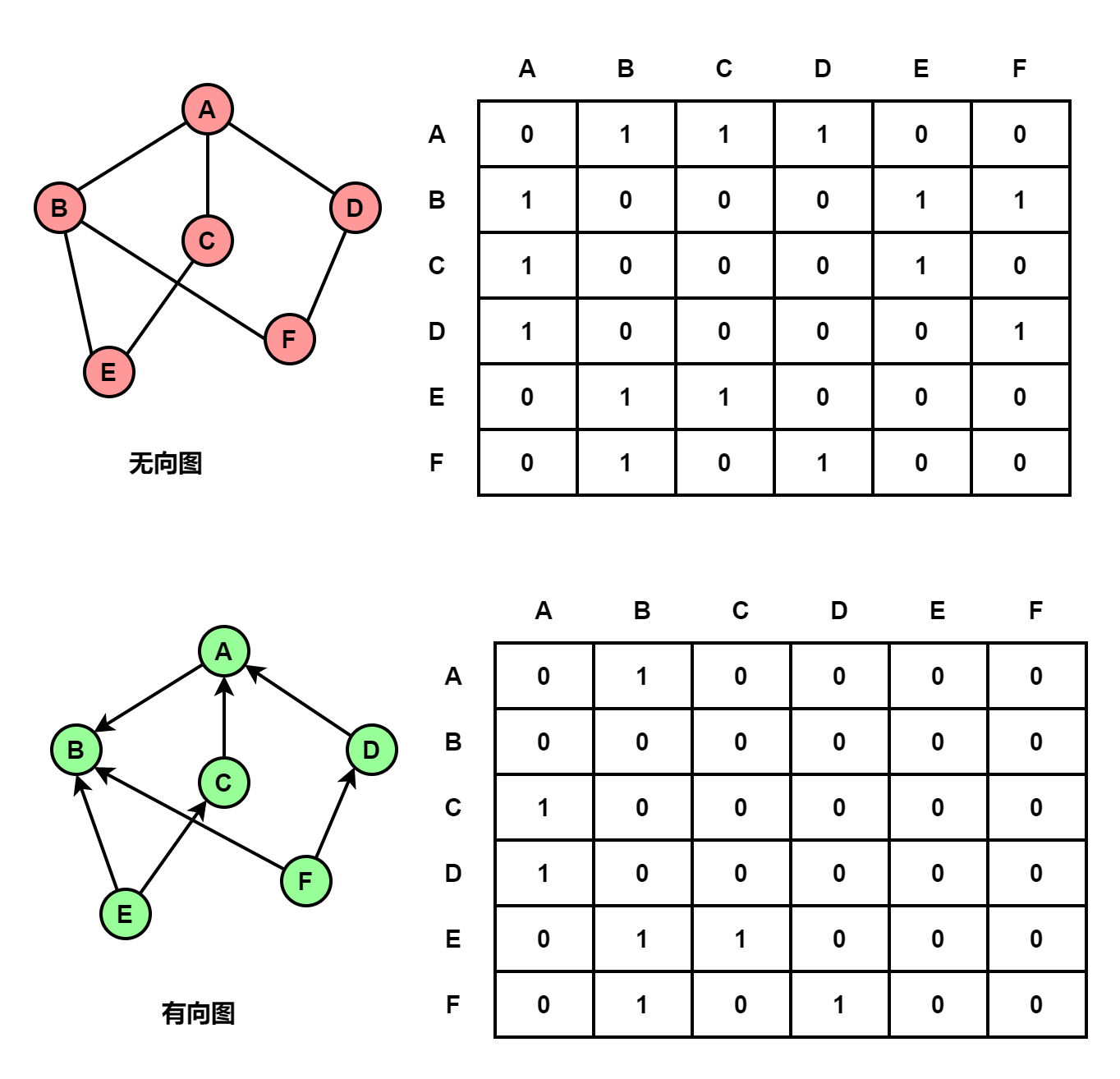
#define MaxSize 100
typedef struct MGraph{
    char Vex[MaxSize];//顶点信息
    int Edge[MaxSize][MaxSize];//邻接矩阵
    int vexnum,arcnum;//顶点数和边数
}MGraph;

$Edge[i][j] = \left\{\begin{matrix} 1 ,(v_i,v_j)或<v_i,v_j>是E(G)中的边\\ 0 ,(v_i,v_j)或<v_i,v_j>不是E(G)中的边 \end{matrix}\right.$

设图G的邻接矩阵为A（矩阵的元素为1\0），则$A^n$元素$A^n[i][j]$表示顶点i到顶点j的长度为n的路径的数目

代码测试

#include <stdio.h>
#include <stdlib.h>
#include<math.h>
 
#define MaxSize 100
#define ElemType int
#define boolean int
#define true 1
#define false 0
 
//邻接矩阵存储无向图的信息
typedef struct MGraph{
    char Vex[MaxSize];//顶点信息
    int Edge[MaxSize][MaxSize];//邻接矩阵
    int vexnum,arcnum;//顶点数和边数
}MGraph;
 
//初始化一个邻接矩阵
boolean MG_Init(MGraph **G){
    *G = (MGraph*)malloc(sizeof(MGraph));
    if((*G) == NULL) return false;//申请空间失败
    (*G)->vexnum = 0;//顶点数为0
    (*G)->arcnum = 0;//边数为0
    // for(int i = 0;i < MaxSize;i++){
    //     for(int j = 0;j < MaxSize;j++){
    //         (*G)->Edge[i][j] = 0;
    //     }
    // }
    return true;
}
 
//获取该结点v的索引
int GetV_Index(MGraph *G,char v){
    for(int i = 0;i<G->vexnum;i++){
        if(G->Vex[i] == v) return i;
    }
    return -1;
}
 
//判断图中是否有结点v
boolean IsVEmpty(MGraph *G,char v){
    for(int i=0;i<G->vexnum;i++){
        if(G->Vex[i] == v) return true;//存在
    }
    return false;//不存在
}
 
//判断图中是否存在该边;传入边
boolean Adjancent(MGraph *G,char v,char w){
    int vi = GetV_Index(G,v);
    int wi = GetV_Index(G,w);
 
    return G->Edge[vi][wi];
}
//判断图中是否存在该边;传入边的索引
boolean Adjancent1(MGraph *G,int vi,int wi){
    if(G->Edge[vi][wi] == 1) return true;
    else return false;
}
 
//插入一个新的顶点
boolean InsertV(MGraph *G,char v){
    if(G->vexnum >= MaxSize || IsVEmpty(G,v)){
        printf("存储顶点数的空间满了或者改结点存在！\n");
        return false;
    }
    G->Vex[G->vexnum++] = v;
    return true;
}
 
//插入边(v,w)
boolean AddEdge(MGraph *G,char v,char w){
    if(!IsVEmpty(G,v) || !IsVEmpty(G,w)){
        printf("输入的边其中有一个顶点或者两个顶点不存在\n");
        return false;
    }
    //获取结点的索引
    int vi = GetV_Index(G,v);
    int wi = GetV_Index(G,w);
    if(Adjancent1(G,vi,wi)){
        printf("该边已经存在\n");
        return false;
    }
    //修改邻接矩阵
    G->Edge[vi][wi] = 1;
    G->Edge[wi][vi] = 1;
    //修改边数
    G->arcnum++;
    return true;
}
 
//删除边(v,w)
boolean RemoveEdge(MGraph *G,char v,char w){
    if(!IsVEmpty(G,v) || !IsVEmpty(G,w)){
        //判断这两个点是否存在
        printf("这两个点不存在\n");
        return false;
    }
    int vi = GetV_Index(G,v);
    int wi = GetV_Index(G,w);
    if(Adjancent1(G,vi,wi) == true){//存在该边就删除
        G->Edge[vi][wi] = 0;
        G->Edge[wi][vi] = 0;
        G->arcnum--;//边减1
        return true;
    }else{
        printf("删除的边不存在\n");
        return false;
    }
}
 
//获取某个结点v的所有邻接边
boolean NeighBors(MGraph *G,char v,char ***res,int *length){
    if(!IsVEmpty(G,v)){
        printf("输入的顶点不存在\n");
        return false;
    }
    int vi = GetV_Index(G,v);
    for(int i = 0;i < G->vexnum;i++){
        if(G->Edge[vi][i] == 1) {
            (*length)++;
        }
    }
    *res = (char **)malloc(sizeof(char)*(*length));
    int index = 0;
    for(int i = 0;i < G->vexnum;i++){
        if(G->Edge[vi][i] == 1) {
            (*res)[index] = (char *)malloc(sizeof(char)*2);
            (*res)[index][0] = v;
            (*res)[index][1] = G->Vex[i];
            index++;
        }
    }
    return true;
}
 
 
int main(){
    MGraph *G;
    MG_Init(&G);
    printf("顶点数：%d；边数：%d\n",G->vexnum,G->arcnum);
    InsertV(G,'A');
    InsertV(G,'B');
    InsertV(G,'C');
    InsertV(G,'D');
    InsertV(G,'E');
    printf("顶点数：%d；边数：%d\n",G->vexnum,G->arcnum);
    AddEdge(G,'A','B');
    AddEdge(G,'C','B');
    AddEdge(G,'C','D');
    AddEdge(G,'A','D');
    AddEdge(G,'A','E');
    printf("顶点数：%d；边数：%d\n",G->vexnum,G->arcnum);
    char **p;
    int length;
    NeighBors(G,'A',&p,&length);
    printf("A的边：");
    for(int i = 0;i < length;i++){
        printf("(%c,%c)，",p[i][0],p[i][1]);
    }
    printf("\n");
    RemoveEdge(G,'A','B');
    printf("顶点数：%d；边数：%d\n",G->vexnum,G->arcnum);
 
    return 0;
}
 
//结果：
顶点数：0；边数：0
顶点数：5；边数：0
顶点数：5；边数：5
A的边：(A,B)，(A,D)，(A,E)，
顶点数：5；边数：4

8.3、邻接表法

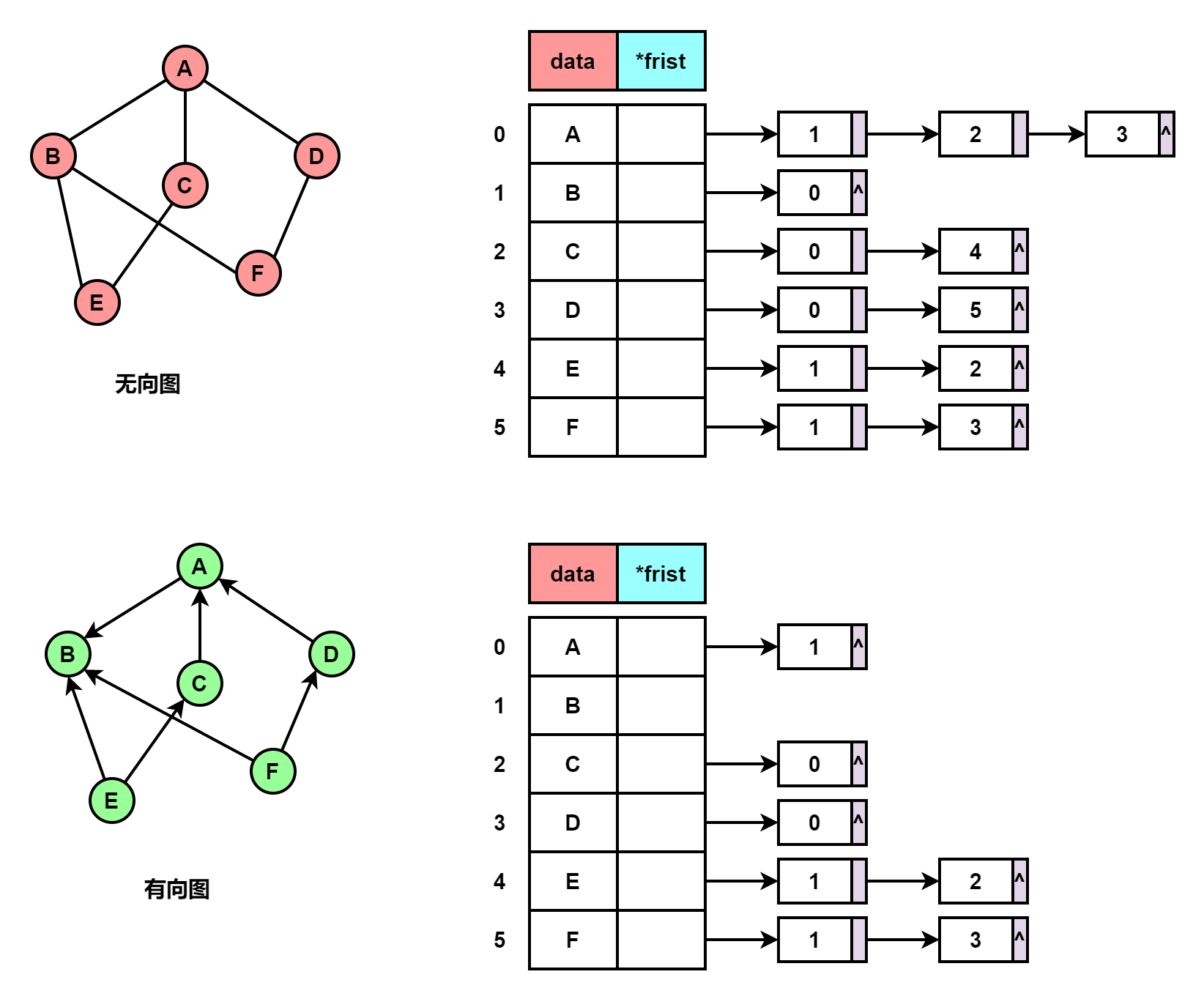
//边\弧
typedef struct ArcNode{
    int adjvex;//边或者弧指向的那个结点
    struct ArcNode *next;//指向下一个弧的指针
   	//int info;//权值
}ArcNode;
 
//顶点
typedef struct VNode{
    ElemType data;//顶点信息
    ArcNode *first;//第一个边或弧
}VNode,AdjList[MaxSize];
 
//图
typedef struct MGraph{
    AdjList vertices;//图的信息
    int vexnum,arcnum;//顶点数和边数
}MGraph;

代码测试

#include <stdio.h>
#include <stdlib.h>
#include<math.h>
 
#define MaxSize 100
#define boolean int
#define true 1
#define false 0
 
//边\弧
typedef struct ArcNode{
    int adjvex;//边或者弧指向的那个结点
    struct ArcNode *next;//指向下一个弧的指针
   	//int info;//权值
}ArcNode;
 
//顶点信息
typedef struct ElemType{
    char v;//顶点信息
    int flag;//顶点是否被使用，1表示使用，0表示未使用
}ElemType;
 
//顶点
typedef struct VNode{
    ElemType data;//顶点信息
    ArcNode *first;//第一个边或弧
}VNode,AdjList[MaxSize];
 
//有向图的邻接表存储
typedef struct MGraph{
    AdjList vertices;//图的信息
    int vexnum,arcnum;//顶点数和边数
}MGraph;
 
//初始化图
boolean MG_Init(MGraph **G){
    (*G) = (MGraph *)malloc(sizeof(MGraph));
    if(*G == NULL){
        printf("内存申请失败！\n");
        return false;
    }
    (*G)->arcnum = 0;//边数
    (*G)->vexnum = 0;//顶点数
    for(int i = 0;i < MaxSize;i++){//把所有带使用的顶点信息数据使用标志全置为0
        (*G)->vertices[i].data.flag = 0;
        (*G)->vertices[i].first = NULL;
    }
    return true;
}
 
//判断顶点V是否存在,并获取边的索引Vi
boolean IsVEmpty(MGraph *G,ElemType V,int *Vi){
    for(int i = 0;i < G->vexnum;i++){
        if(G->vertices[i].data.v == V.v && G->vertices[i].data.flag == 1) {
            *Vi = i;
            return true;
        }
    }
    return false;
}
 
//判断边是否存在:
boolean Adjancent(MGraph *G,ElemType V,ElemType W,int *Vi,int *Wi){
    if(!IsVEmpty(G,V,Vi) || !IsVEmpty(G,W,Wi)){
        printf("其中一个顶点不存在!!/\n");
        return true;
    }
    ArcNode *node = G->vertices[*Vi].first;
    while(node != NULL){
        if(node->adjvex == *Wi){
            // printf("边已经存在\n");
            return true;
        }
        node = node->next;
    }
    return false;
}
 
//插入顶点
boolean InsertV(MGraph *G,ElemType V){
    int *Vi;
    if(IsVEmpty(G,V,Vi)){
        printf("顶点已经存在！！\n");
        return false;
    }
    V.flag = 1;
    G->vertices[G->vexnum++].data = V;
    return true;
}
 
//插入边
boolean AddArcNode(MGraph *G,ElemType V,ElemType W){
    int *Vi = (int *)malloc(sizeof(int));
    int *Wi = (int *)malloc(sizeof(int));
    if(Adjancent(G,V,W,Vi,Wi)){//判断边是否存在
        return false;
    }
    ArcNode * p = (ArcNode*)malloc(sizeof(ArcNode));
    p->adjvex = *Wi;
    p->next = NULL;
    if(G->vertices[*Vi].first == NULL){//没有边，新增加边
        G->vertices[*Vi].first = p;
        G->arcnum++;
        return true;
    }
    ArcNode *node = G->vertices[*Vi].first;
    while(node->next != NULL){
        node = node->next;
    }
    node->next = p;
    G->arcnum++;
    return true;
}
 
//获取某个结点v的所有邻接边;<v,wi>;以v为尾巴
boolean NeighBors(MGraph *G,ElemType V,ElemType ***res,int *length){
    int *Vi = (int *)malloc(sizeof(int));
    if(!IsVEmpty(G,V,Vi)){
        return false;
    }
    ArcNode *node = G->vertices[*Vi].first;
    while(node != NULL){
        (*length)++;
        node = node->next;
    }
    *res = (ElemType **)malloc(sizeof(ElemType)*(*length));
    node = G->vertices[*Vi].first;
    for(int i=0;i < (*length) ;i++){
        (*res)[i] = (ElemType *)malloc(sizeof(ElemType)*2);
        (*res)[i][0] = V;
        (*res)[i][1] = G->vertices[node->adjvex].data;
        node = node->next;
    }
    return true;
}
 
//移除该边<V,W>
boolean RemoveArcNode(MGraph *G,ElemType V,ElemType W){
    int *Vi = (int *)malloc(sizeof(int));
    int *Wi = (int *)malloc(sizeof(int));
    if(!Adjancent(G,V,W,Vi,Wi)){//判断该边是否存在
        return false;
    }
    ArcNode *delete = G->vertices[*Vi].first;//删除的结点
    ArcNode *pre = NULL;//删除边的前一个结点
    while(delete != NULL){//寻找删除的边
        if(delete->adjvex == *Wi){
            break;
        }
        pre = delete;
        delete = delete->next;
    }
    if(pre == NULL){
        G->vertices[*Vi].first = G->vertices[*Vi].first->next;
    }else{
        pre->next = delete->next;//修改指针
    }
    G->arcnum--;//修改边数
    free(delete);//释放内存
 
    return true;
}
 
//删除顶点
boolean DeleteV(MGraph *G,ElemType V){
    int *Vi = (int *)malloc(sizeof(int));
    if(!IsVEmpty(G,V,Vi)){
        return false;
    }
    ArcNode *W = G->vertices[*Vi].first;
    while(W != NULL){
        RemoveArcNode(G,V,G->vertices[G->vertices[*Vi].first->adjvex].data);
        W = G->vertices[*Vi].first;
    }
    int index = 0;
    int sum = 0;
    while(sum < G->vexnum){
        if(G->vertices[index].data.flag==1){
            W = G->vertices[index].first;
            while(W != NULL){
                if(W->adjvex == *Vi){
                    RemoveArcNode(G,G->vertices[index].data,V);
                    break;
                }
                W = W->next;
            }
            sum++;
        }
        index++;
    }
    G->vertices[*Vi].data.flag = 0;
    G->vexnum--;
    return true;
}
 
 
 
int main(){
    MGraph *G;
    MG_Init(&G);
    printf("顶点数：%d；边数：%d\n",G->vexnum,G->arcnum);
    ElemType V1;
    V1.v = 'A';
    InsertV(G,V1);
    ElemType V2;
    V2.v = 'B';
    InsertV(G,V2);
    ElemType V3;
    V3.v = 'C';
    InsertV(G,V3);
    ElemType V4;
    V4.v = 'D';
    InsertV(G,V4);
    printf("顶点数：%d；边数：%d\n",G->vexnum,G->arcnum);
    AddArcNode(G,V1,V2);
    AddArcNode(G,V1,V3);
    AddArcNode(G,V2,V4);
    AddArcNode(G,V4,V1);
    AddArcNode(G,V4,V3);
    AddArcNode(G,V4,V2);
    printf("顶点数：%d；边数：%d\n",G->vexnum,G->arcnum);
    ElemType **p;
    int length;
    NeighBors(G,V1,&p,&length);
    printf("%c为尾的边：",V1.v);
    for(int i = 0; i < length;i++){
        printf("<%c,%c>,",p[i][0].v,p[i][1].v);
    }
    printf("\n");
    RemoveArcNode(G,V4,V2);
    printf("顶点数：%d；边数：%d\n",G->vexnum,G->arcnum);
 
    DeleteV(G,V1);
    printf("顶点数：%d；边数：%d\n",G->vexnum,G->arcnum);
 
    return 0;
}
//结果：
顶点数：0；边数：0
顶点数：4；边数：0
顶点数：4；边数：6
A为尾的边：<A,B>,<A,C>,
顶点数：4；边数：5
顶点数：3；边数：2

8.4、十字链表法存储有向图

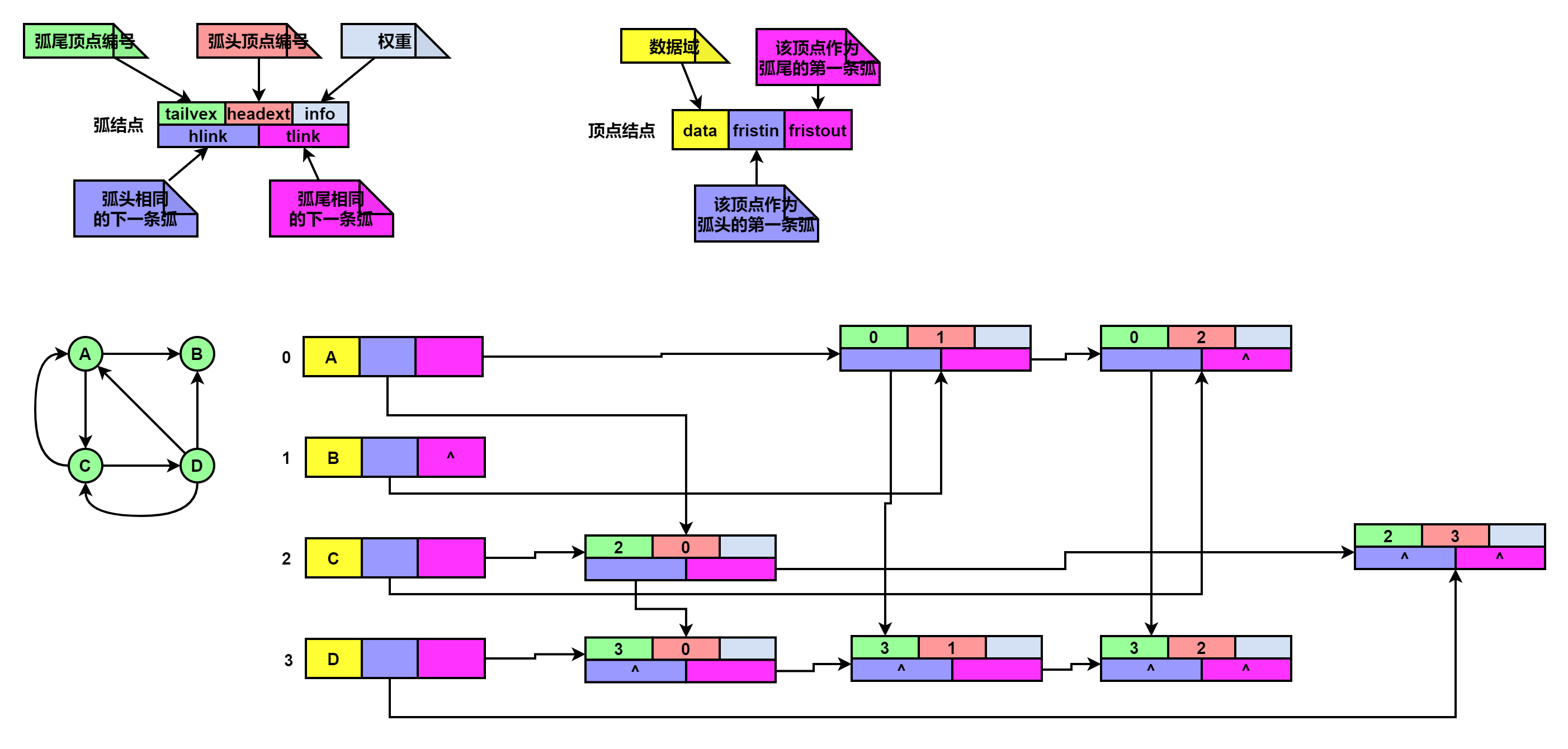
#define MaxSize 100
//弧结点
typedef struct ArcNode{
    int tailvex,headvex;//弧尾号，弧头号
    //int info;//权值
    struct ArcNode *hlink,*tlink;//弧头的下一个弧，弧尾的下一个弧
}ArcNode;
 
//顶点结点
typedef struct VNode{
    ElemType data;//顶点信息
    ArcNode * fristin,*fristout;//弧头的第一个弧，弧尾的第一个弧
}VNode,AdjList[MaxSize];
 
//图
typedef struct MGraph{
    AdjList vertices;//图的信息
    int vexnum,arcnum;//顶点数和边数
}MGraph;

注意：十字链表法只能用于存储有向图

8.5、邻接多重表

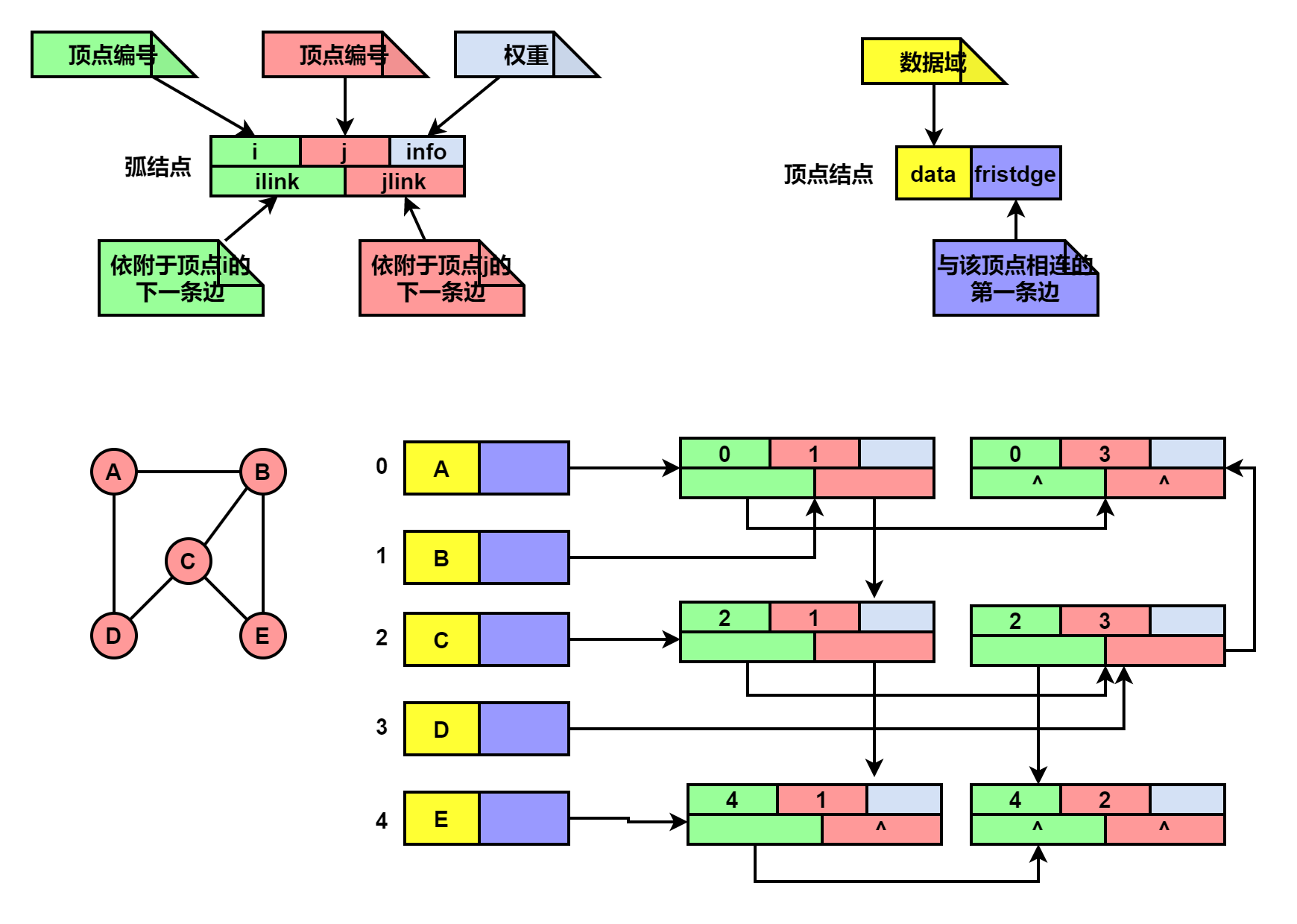
#define MaxSize 100
//弧结点
typedef struct ArcNode{
    int i,j;//顶点
    //int info;//权值
    struct ArcNode *ilink,*jlink;//依附于i的一条边，依附于j的第一条边
}ArcNode;
 
//顶点结点
typedef struct VNode{
    ElemType data;//顶点信息
    ArcNode * fristdge;//与顶点相邻的第一条边
}VNode,AdjList[MaxSize];
 
//图
typedef struct MGraph{
    AdjList vertices;//图的信息
    int vexnum,arcnum;//顶点数和边数
}MGraph;

注意：邻接多重表只能存储无向图