数据结构 栈

3、栈

王道计算机考研 数据结构 来自哔哩哔哩

栈（Stack）是只允许在一端插入或删除操作的线性表

LIFO（后进先出）

n个不同的元素进栈，出栈的顺序有$\frac{1}{n+1} C_{2n}^{n} $个，卡特兰（Catalan）数

3.1、顺序栈

栈的定义

#include <stdio.h>
#include <stdlib.h>

#define MaxSize 10
#define ElemType int
#define true 1
#define fales 0

//顺序表定义栈的结构体
typedef struct{
    ElemType data[MaxSize];
    int top;
}SqStack;

//初始化一个栈
ElemType InitStack(SqStack *S){
    S->top = -1;  //栈顶元素指向-1
    return true;
}

入栈、出栈、读取栈顶元素

//入栈操作
ElemType Push(SqStack *S,ElemType e){
    if(S->top == MaxSize-1) return fales;   //边界判断
    S->data[++S->top] = e;  //先栈顶+!,在赋值操作
    return true;
}

//栈顶元素弹出
ElemType Pop(SqStack *S,ElemType *e){
    if(S->top == -1) return fales;  //栈中没有元素
    *e = S->data[S->top--];  //先弹栈在栈顶-1
    return true;
}

//读取栈顶元素
ElemType GetTop(SqStack S,ElemType *e){
    if(S.top == -1) return false;  //栈中没有元素
    *e = S.data[S.top];
    return true;
}

3.2、链栈

栈的定义

#include <stdio.h>
#include <stdlib.h>

#define ElemType int
#define true 1
#define false 0

//定义一个链栈
typedef struct LinkNode
{
    ElemType data;
    struct LinkNode *next;
} *LinkStack,LinkNode;

//初始化一个不带头结点的栈
ElemType InitStack(LinkStack *S){
    // *S = (LinkStack)malloc(sizeof(LinkNode));
    *S = NULL;
    return true;
}

//判断栈是否为空
ElemType Empty(LinkStack S){
    if(S == NULL) return false;
    else true;
}

入栈、出栈

//入栈
ElemType Push(LinkStack *S,ElemType e){
    LinkNode *p = (LinkNode *)malloc(sizeof(LinkNode));
    if(p == NULL) return false;
    p->data = e;
    p->next = *S;
    *S = p;
    return true;
}

//弹栈
ElemType Pop(LinkStack *S,ElemType *e){
    if(*S == NULL) return false;
    *e = (*S)->data;
    (*S) = (*S)->next;
    return true;
}

头插法

3.3、括号匹配

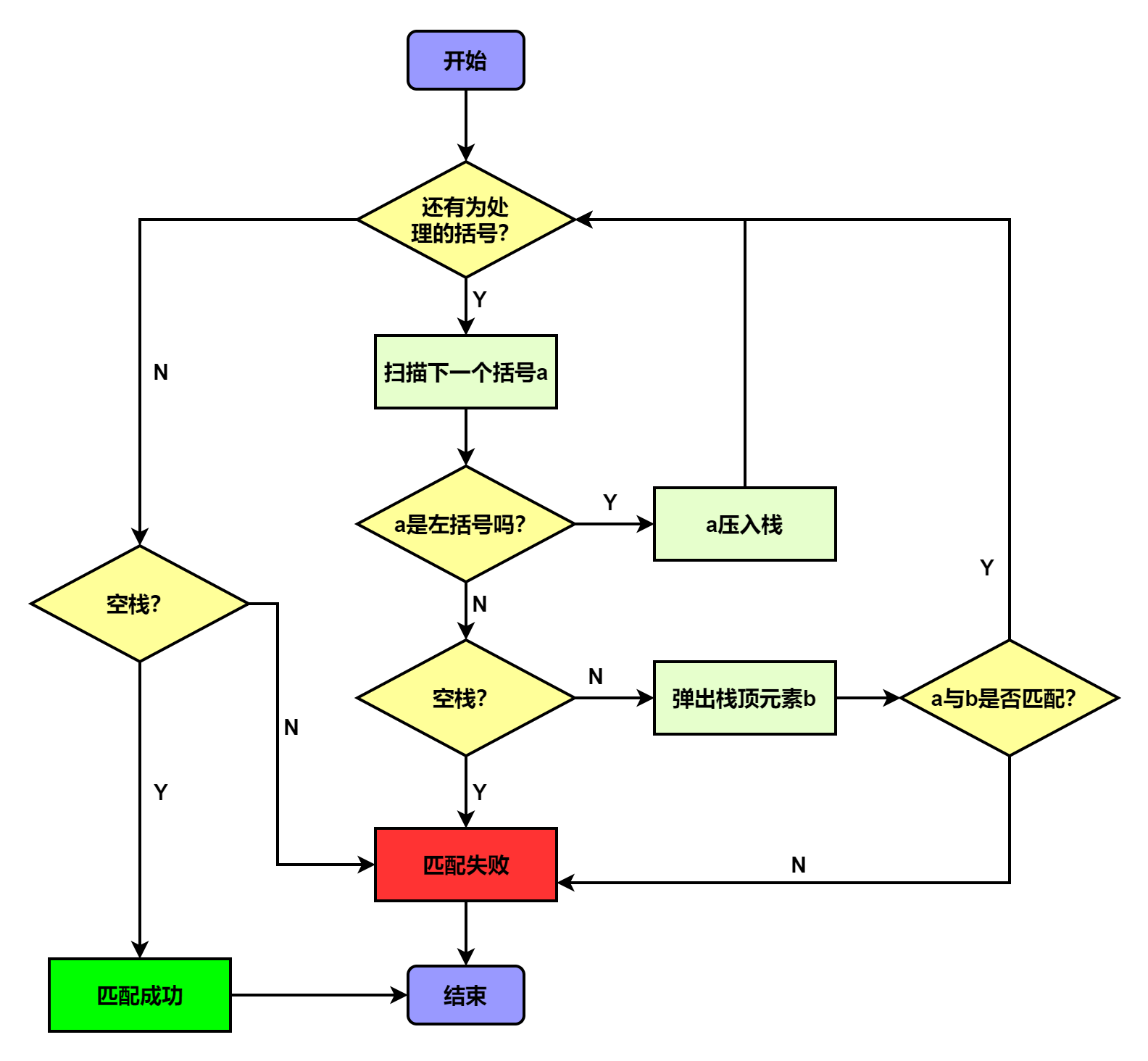
代码

#include <stdio.h>
#include <stdlib.h>

#define MaxSize 10
#define ElemType char
#define true 1
#define false 0

//顺序表定义栈的结构体
typedef struct{
    ElemType data[MaxSize];
    int top;
}SqStack;

//判断栈是否为空
int StackEmpty(SqStack S){
    if(S.top == -1) return true;
    else return false;
}

//初始化一个栈
ElemType InitStack(SqStack *S){
    S->top = -1;  //栈顶元素指向-1
    return true;
}

//入栈操作
ElemType Push(SqStack *S,ElemType e){
    if(S->top == MaxSize-1) return false;   //边界判断
    S->data[++S->top] = e;  //先栈顶+!,在赋值操作
    return true;
}

//栈顶元素弹出
ElemType Pop(SqStack *S,ElemType *e){
    if(S->top == -1) return false;  //栈中没有元素
    *e = S->data[S->top--];  //先弹栈在栈顶-1
    return true;
}

//读取栈顶元素
ElemType GetTop(SqStack S,ElemType *e){
    if(S.top == -1) return false;  //栈中没有元素
    *e = S.data[S.top];
    return true;
}

//括号匹配算法
int bracketCheck(char str[],int length){
    SqStack S;		//定义栈
    InitStack(&S);	//初始化栈
    for(int i=0;i<length;i++){
        if(str[i] == '(' || str[i] == '{' || str[i] == '['){
            Push(&S,str[i]);	//左括号入栈
        }else{
            if(StackEmpty(S)) return false;	//判断栈是否为空
            char topElem;
            Pop(&S,&topElem);	//右括号出栈
            if(str[i] == ')' && topElem != '(') return false;
            if(str[i] == '}' && topElem != '{') return false;
            if(str[i] == ']' && topElem != '[') return false;
        }
    }
    return StackEmpty(S);
}

int main(){
    char str[] = {'(','(','[',']','{','}',')',')'};
    int flag = bracketCheck(str,8);
    printf("括号是否匹配：%d\n",flag);
    return 0;
}

//结果
括号是否匹配：1

3.4、表达式求值问题