CF506E Mr. Kitayuta's Gift 题解

https://codeforces.ml/contest/506/problem/E

题意：

给定字符串 \(S\) ，只包含小写英文字母，求再插入 \(N\) 个小写英文字母使得 \(S\) 成为回文串的方案数。对 \(10007\) 取模。

数据范围： \(1\le|S|\le 200,1\le N\le 10^9\) 。

题解:

不妨令 \(M=|S|\) 。

先考虑 \(N+M\) 为偶数的情况：

朴素 DP :

并不是很难……

设 \(F(l,r,i)\) 为原字符串 \([l,r]\) 还没被匹配完，最终字符串前 \(i\) 位和后 \(i\) 位被匹配完的方案数。

设 \(G_i\) 为最终前 \(i\) 位和后 \(i\) 位和原字符串均被被匹配完的方案数。

• 转移：

  • \(S_l=S_r\) 且 \(r-l\le 1\) ：

    \(G_{i+1}\leftarrow F(l,r,i)\) （选择 \(S_l\) ）

    \(F(l,r,i+1)\leftarrow 25\times F(l,r,i)\) （选择其它字母）

  • \(S_l=S_r\) 且 \(r-l>1\) ：

    \(F(l+1,r-1,i+1)\leftarrow F(l,r,i)\) （选择 \(S_l\) ）

    \(F(l,r,i+1)\leftarrow 25\times F(l,r,i)\) （选择其它字母）

  • \(S_l\not= S_r\) ：

    \(F(l,r-1,i+1)\leftarrow F(l,r,i)\) （选择 \(S_r\) ）

    \(F(l+1,r,i+1)\leftarrow F(l,r,i)\) （选择 \(S_l\) ）

    \(F(l,r,i+1)\leftarrow 24 \times (l,r,i)\) （选择其它字母）

  • 对于 \(G\) ： \(G_{i}\leftarrow 26\times G_{i-1}\)

这个东西可以用矩阵优化一下，时间复杂度： \(O(M^6\log N)\) 。

显然是过不了的！！！

有限状态自动机

在做矩阵快速幂时，只要 \((l,r)\) 相同就是同一个状态。

实际上求的是所有长度为 \(\frac{N+M}{2}\) 的路径。

这张图长得很奇怪，除开最后一个点是向自己连了 \(26\) 个自环，其余的不是向自己连了 \(24\) 个，就是 \(25\) 个。

显然是会经过最后一个点的。

这条路径上大部分是自环，对于不是自环的，如果是 \(24\) 点，则长度减 \(1\) ，否则减 \(2\) （根据 DP 式子）。

所以如果知道了 \(24\) 点的个数，就知道这条路径是由哪些点构成的。

即一条路径上有 \(x\) 条 \(24\) 点，就会有 \(\left \lceil \frac{n-x}{2} \right \rceil\) 个 \(25\) 点。

实际上，只要知道这些点的数目，路径的数量和点的顺序是无关的，只需要分别求出路径数量和等价类的个数。

对于每一条长这样的链分别求，等价类可以用记忆化搜索求。

时间复杂度： \(O(M^4\log N)\) 。仍然过不去。

压缩自动机

注意到对每一条链分别求非常不优美，考虑合并起来。

这个合并非常简单，放一张图：

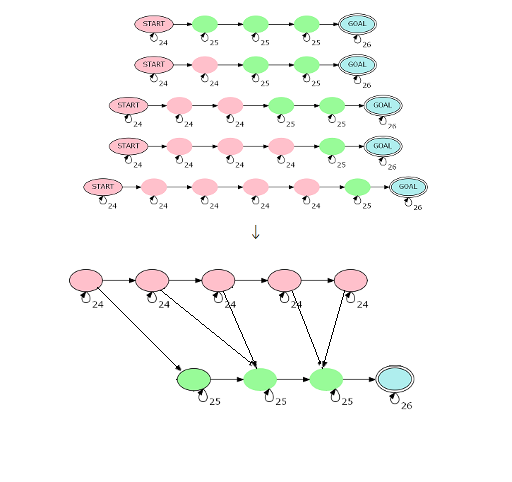
需要注意可以从第一个绿点出发。

时间复杂度： \(O(M^3\log N)\) 。

奇数的情况

其实大体和偶数是差不多的，但是有一种情况不行：

到了最后一步，只能放一个字符了，但是此时 \(r-l=2\) ，要将 \(S_l\) 和 \(S_r\) 都放进去。

只需要把这种情况减掉。重新建图，最后一步转移只能用这种方法，且终点没有自环，使得刚好在最后一步。

卡常

据说有一点卡常？注意到自动机是一个 DAG 且转移顺序恰好是由小到大，因此矩阵乘法时可以弄成一个上三角矩阵。

常数减小为 \(\frac{1}{6}\) 。

代码：

#include <bits/stdc++.h>
using namespace std;
const int N=205,M=305,mod=10007;
int n,m,sz,ans,st,f[N][N][N];
char s[N];
struct mat{
	int v[M][M];
	void clear() {memset(v,0,sizeof(v));}
	mat() {clear();}
	mat operator * (const mat&x) const {
		mat res;
		for(int i=1;i<=sz;i++)
			for(int k=1;k<=i;k++)
				for(int j=1;j<=k;j++) (res.v[i][j]+=v[i][k]*x.v[k][j])%=mod;
		return res;
	}
}p,lst;
int dp(int x,int l,int r){
	if(x<0) return 0;
	int&d=f[x][l][r];if(~d) return d;
	if(l==1&&r==m) return d=(!x);
	d=0;
	if(l!=1&&s[l-1]!=s[r]) (d+=dp(x-1,l-1,r))%=mod;
	if(r!=m&&s[l]!=s[r+1]) (d+=dp(x-1,l,r+1))%=mod;
	if(l!=1&&r!=m&&s[l-1]==s[r+1]) (d+=dp(x,l-1,r+1))%=mod;
	return d;
}
signed main(){
	scanf("%s%d",s+1,&n);m=strlen(s+1);sz=m+(m+1)/2;
	memset(f,-1,sizeof(f));
	for(int i=0;i<m;i++){
		int cnt=0;
		for(int j=1;j<=m;j++) (cnt+=dp(i,j,j))%=mod;
		for(int j=1;j<m;j++)
			if(s[j]==s[j+1]) (cnt+=dp(i,j,j+1))%=mod;
		if(i) p.v[sz-(m-i+1)/2][i]=cnt;
		else st=cnt;
	}
	for(int i=2;i<m;i++) p.v[i][i-1]=1;
	for(int i=m;i<sz;i++) p.v[i+1][i]=1;
	for(int i=1;i<m;i++) p.v[i][i]=24;
	for(int i=m;i<sz;i++) p.v[i][i]=25;
	p.v[sz][sz]=26;
	for(int i=1;i<=sz;i++) lst.v[i][i]=1;
	for(int i=(n+m+1)/2;i;i>>=1,p=p*p)
		if(i&1) lst=lst*p;
	if(m>1) ans=lst.v[sz][1];(ans+=st*lst.v[sz][m])%=mod;
	if((n+m)%2==0) return printf("%d\n",ans),0;
	lst.clear();p.clear();
	for(int i=0;i<m;i++){
		int cnt=0;
		for(int j=1;j<m;j++)
			if(s[j]==s[j+1]) (cnt+=dp(i,j,j+1))%=mod;
		if(i) p.v[sz-(m-i+1)/2][i]=cnt;
		else st=cnt;
	}
	for(int i=2;i<m;i++) p.v[i][i-1]=1;
	for(int i=m;i<sz;i++) p.v[i+1][i]=1;
	for(int i=1;i<m;i++) p.v[i][i]=24;
	for(int i=m;i<sz;i++) p.v[i][i]=25;
	for(int i=1;i<=sz;i++) lst.v[i][i]=1;
	for(int i=(n+m+1)/2;i;i>>=1,p=p*p)
		if(i&1) lst=lst*p;
	if(m>1) ans-=lst.v[sz][1];(ans-=st*lst.v[sz][m])%=mod;
	printf("%d\n",(ans+mod)%mod);
	return 0;
}