深度学习教程 | 浅层神经网络

作者：韩信子@ShowMeAI
教程地址：https://www.showmeai.tech/tutorials/35
本文地址：https://www.showmeai.tech/article-detail/214
声明：版权所有，转载请联系平台与作者并注明出处

收藏ShowMeAI查看更多精彩内容

第1门课神经网络和深度学习，第3周：浅层神经网络

本系列为吴恩达老师《深度学习专项课程(Deep Learning Specialization)》学习与总结整理所得，对应的课程视频可以在这里查看。

引言

在ShowMeAI前一篇文章 神经网络基础 中我们对以下内容进行了介绍：

二分类问题、逻辑回归模型及损失函数。
梯度下降算法。
计算图与正向传播及反向传播。
向量化方式并行计算与提效。

本篇内容我们将从浅层神经网络入手，逐步拓展到真正的神经网络模型知识学习。

1.神经网络表示

神经网络的表示 Neural Network Representation

图示为两层神经网络，也可以称作单隐层神经网络(a single hidden layer neural network)。这就是典型的浅层(shallow)神经网络，结构上，从左到右，可以分成三层：

输入层(input layer)：竖向堆叠起来的输入特征向量。
隐藏层(hidden layer)：抽象的非线性的中间层。
输出层(output layer)：输出预测值。

注意：当我们计算网络的层数时，通常不考虑输入层。因此图中隐藏层是第一层，输出层是第二层。

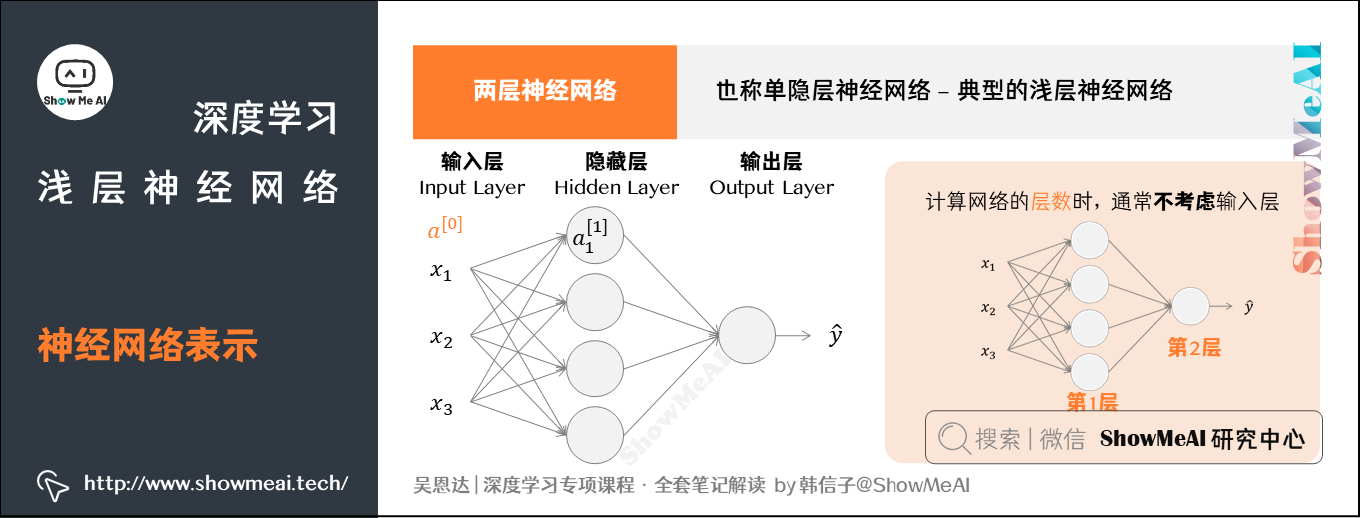
神经网络表示

有一些约定俗成的符号表示，如下：

输入层的激活值为 $a^{[0]}$ ，隐藏层产生的激活值，记作 $a^{[1]}$ 。
隐藏层的第一个单元(或者说节点)就记作 $a^{[1]}_1$ ，输出层同理。
隐藏层和输出层都是带有参数 $W$ 和 $b$ 的，它们都使用上标[1]来表示是和第一个隐藏层有关，或者上标[2]来表示是和输出层有关。

2.计算神经网络的输出

2.1 两层神经网络

计算一个神经网络的输出 Computing a Neural Network's Output

接下来我们开始详细推导神经网络的计算过程。

我们依旧来看看我们熟悉的逻辑回归，我们用其构建两层神经网络。逻辑回归的前向传播计算可以分解成计算 $z$ 和 $a$ 的两部分。

如果我们基于逻辑回归构建两层神经网络，前向计算从前往后要做2次计算：

从输入层到隐藏层，对应一次逻辑回归运算。
从隐藏层到输出层，对应一次逻辑回归运算。

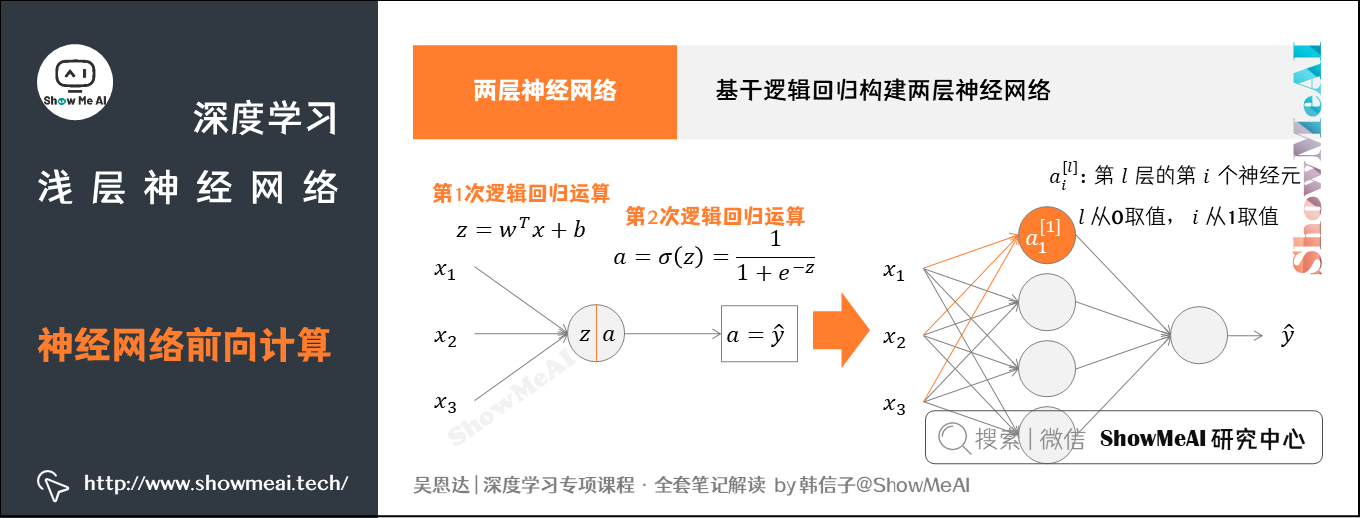
神经网络前向计算

在每层计算中，我们注意对应的上标和下标：

我们记上标方括号 $^{[ ]}$ 表示layer，记下标表示第几个神经元。例如， $a_i^{[l]}$ 表示第 $l$ 层的第 $i$ 个神经元。
注意， $i$ 从 $1$ 开始， $l$ 从 $0$ 开始。

2.2 单个样本计算方式

我们将输入层到隐藏层的计算公式列出来：

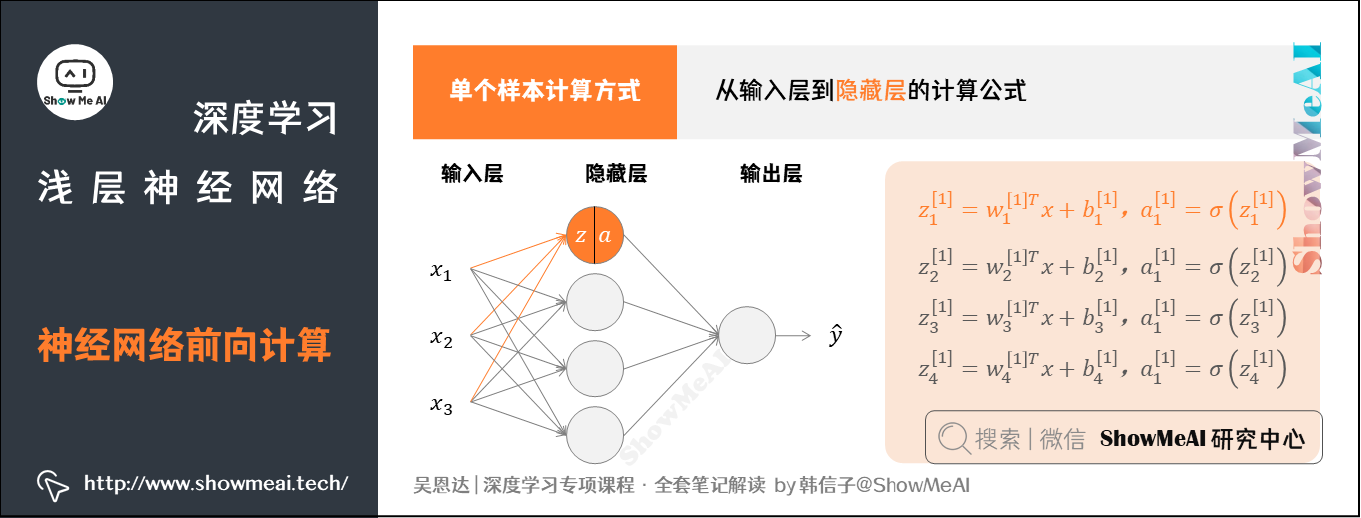
神经网络前向计算

后续从隐藏层到输出层的计算公式为：

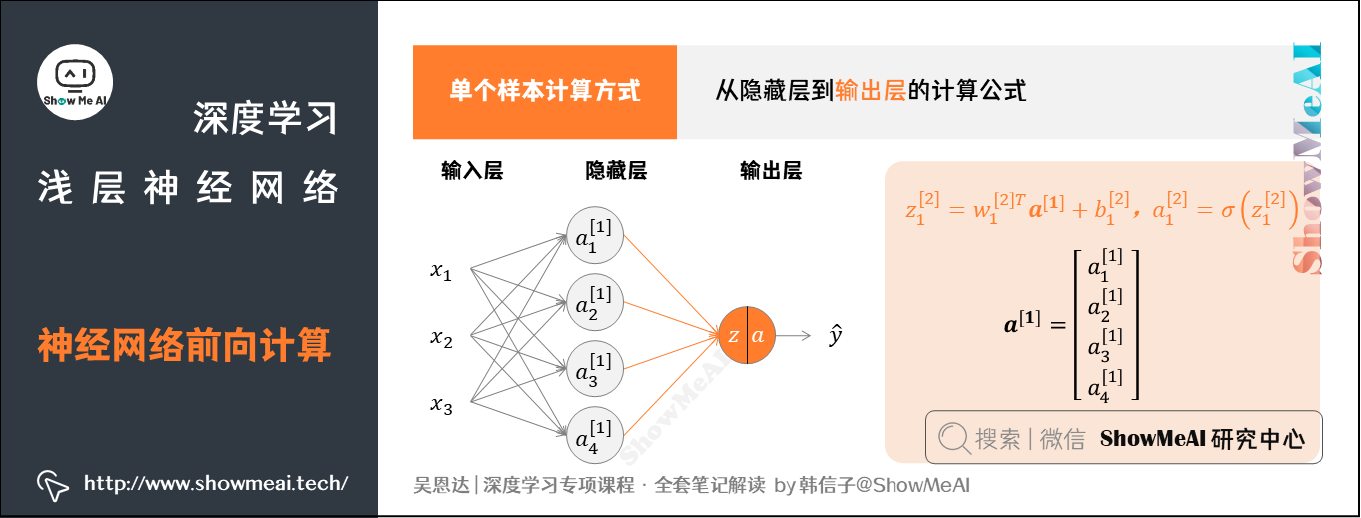
神经网络前向计算

上述每个节点的计算都对应着一次逻辑运算的过程，分别由计算 $z$ 和 $a$ 两部分组成。

2.3 向量化计算

多样本向量化 Vectorizing across Multiple Examples

我们引入向量化思想提升计算效率，将上述表达式转换成矩阵运算的形式，如下所示：

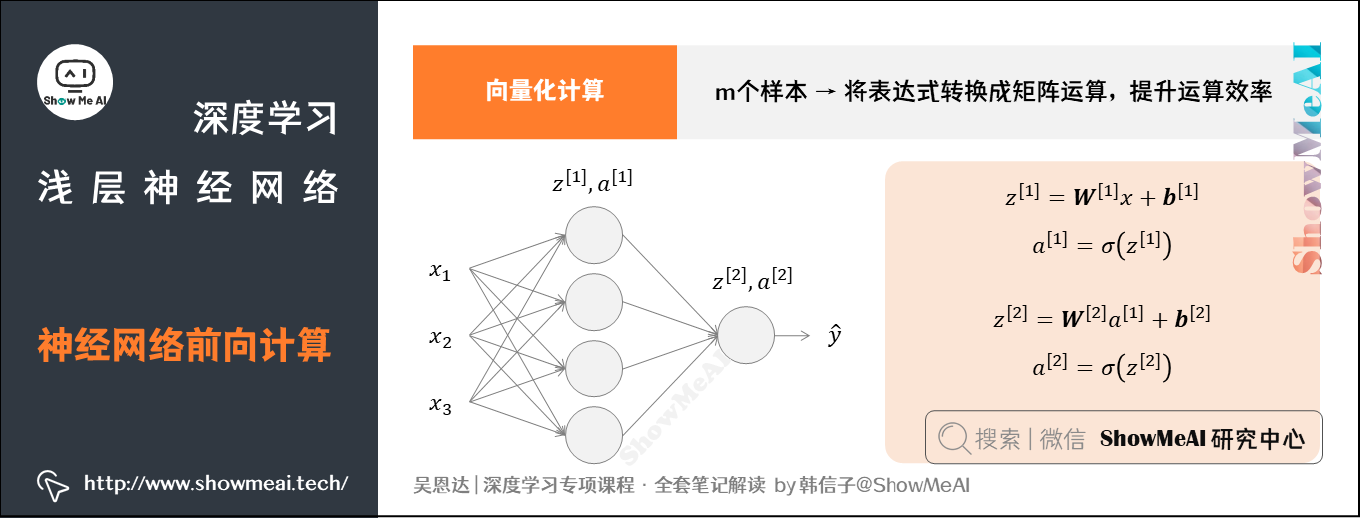
神经网络前向计算

我们这里特别注意一下数据维度：

$W^{[1]}$ 的维度是 $(4,3)$
$b^{[1]}$ 的维度是 $(4,1)$
$W^{[2]}$ 的维度是 $(1,4)$
$b^{[2]}$ 的维度是 $(1,1)$

2.4 数据集向量化计算

向量化实现的解释 Justification for Vectorized Implementation

上面部分提到的是单个样本的神经网络正向传播矩阵运算过程。对于 $m$ 个训练样本，我们也可以使用向量化矩阵运算的形式来提升计算效率。形式上，它和单个样本的矩阵运算十分相似，比较简单。我们记输入矩阵 $X$ 的维度为 $(n_x,m)$ ，则有：

神经网络前向计算

上述公式中， $Z^{[1]}$ 的维度是 $(4,m)$ ，4是隐藏层神经元的个数； $A^{[1]}$ 的维度与 $Z^{[1]}$ 相同； $Z^{[2]}$ 和 $A^{[2]}$ 的维度均为 $(1,m)$ 。

我们可以这样理解上述的矩阵：行表示神经元个数，列表示样本数目 $m$ 。

3.激活函数

激活函数 Activation Functions

3.1 不同的激活函数与选择

在神经网络中，隐藏层和输出层都需要激活函数(activation function)，前面的例子中我们都默认使用Sigmoid函数 $\sigma(z)$ 作为激活函数。实际我们有不同的激活函数可以选择，而且它们有各自的优点：

激活函数

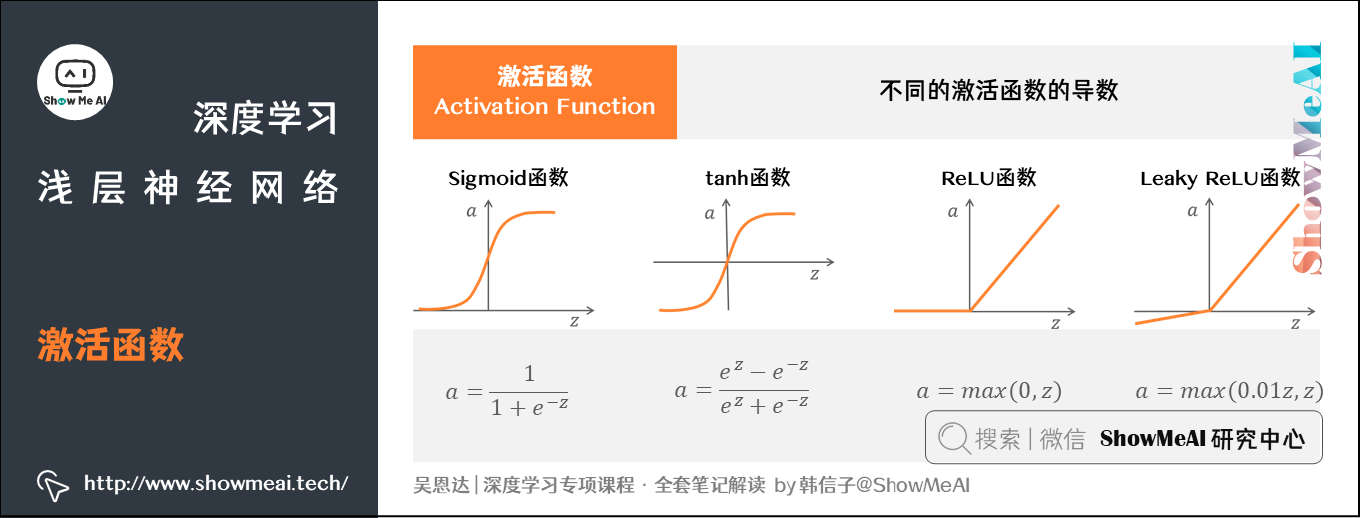
(1) tanh 函数

the hyperbolic tangent function，双曲正切函数

a = \frac{e^{z} - e^{- z}}{e^{z} + e^{- z}}

$a = \frac{e^z - e^{-z}}{e^z + e^{-z}}$

优点：函数输出介于 $(-1,1)$ ，激活函数的平均值就更接近0，有类似数据中心化的效果。效果几乎总比Sigmoid函数好(二元分类的输出层我们还是会用Sigmoid，因为我们希望输出的结果介于 $(0,1)$ )。

缺点：当 $z$ 趋紧无穷大(或无穷小)，导数的梯度(即函数的斜率)就趋紧于0，这使得梯度算法的速度大大减缓。这一点和Sigmoid一样。

(2) ReLU函数

the rectified linear unit，修正线性单元

a = m a x (0, z)

$a=max(0,z)$

优点：当 $z > 0$ 时，梯度始终为1，从而提高神经网络基于梯度算法的运算速度，收敛速度远大于Sigmoid和tanh。

缺点：当 $z < 0$ 时，梯度一直为0，但是实际的运用中，该缺陷的影响不是很大。

(3) Leaky ReLU

带泄漏的ReLU

a = m a x (0.01 z, z)

$a=max(0.01z,z)$

优点：Leaky ReLU保证在 $z < 0$ 的时候，梯度仍然不为0。

理论上来说，Leaky ReLU有ReLU的所有优点，但在实际操作中没有证明总是好于ReLU，因此不常用。

总结

在选择激活函数的时候，如果在不知道该选什么的时候就选择ReLU。当然也没有固定答案，要依据实际问题在交叉验证集合中进行验证分析。注意，我们可以在不同层选用不同的激活函数。

3.2 使用非线性激活函数的原因

为什么需要非线性激活函数？ Why Need a Nonlinear Activation Function?

使用线性激活函数和不使用激活函数、无论神经网络有多少层，输出都是输入的线性组合，与没有隐藏层效果相当，就成了最原始的感知器了。我们以2层神经网络做一个简单推导，如下：

假设所有的激活函数都是线性的，为了更简单一点，我们直接令激活函数 $g(z)=z$ ，即 $a=z$ 。那么，浅层神经网络的各层输出为：

z^{[1]} = W^{[1]} x + b^{[1]}

$z^{[1]}=W^{[1]}x+b^{[1]}$

a^{[1]} = z^{[1]}

$a^{[1]}=z^{[1]}$

z^{[2]} = W^{[2]} a^{[1]} + b^{[2]}

$z^{[2]}=W^{[2]}a^{[1]}+b^{[2]}$

a^{[2]} = z^{[2]}

$a^{[2]}=z^{[2]}$

我们对上述公式中 $a^{[2]}$ 展开计算，得：

\begin{aligned} a^{[2]} = z^{[2]} & = W^{[2]} a^{[1]} + b^{[2]} \\ = W^{[2]} (W^{[1]} x + b^{[1]}) + b^{[2]} \\ = (W^{[2]} W^{[1]}) x + (W^{[2]} b^{[1]} + b^{[2]}) \\ = W^{'} x + b^{'} \end{aligned}

$\begin{aligned} a^{[2]}=z^{[2]} &=W^{[2]} a^{[1]}+b^{[2]} \\ &=W^{[2]}\left(W^{[1]} x+b^{[1]}\right)+b^{[2]} \\ &=\left(W^{[2]} W^{[1]}\right) x+\left(W^{[2]} b^{[1]}+b^{[2]}\right) \\ &=W^{\prime} x+b^{\prime} \end{aligned}$

上述推导后，我们可以发现 $a^{[2]}$ 仍是输入变量 $x$ 的线性组合！后续堆叠更多的层次，也可以依次类推，这表明，使用神经网络，如果不使用激活函数或使用线性激活函数，与直接使用线性模型的效果并没有什么两样！因此，隐藏层的激活函数必须要是非线性的。

不过，在部分场景下，比如是回归预测问题而不是分类问题，输出值 $y$ 为连续值，输出层的激活函数可以使用线性函数。如果输出 $y$ 恒为正值，则也可以使用ReLU激活函数，这些具体情况具体分析。

3.3 激活函数的导数

激活函数的导数 Derivatives of Activation Functions

我们来看一下不同激活函数的导数，这将在我们反向传播中频繁用到。

激活函数

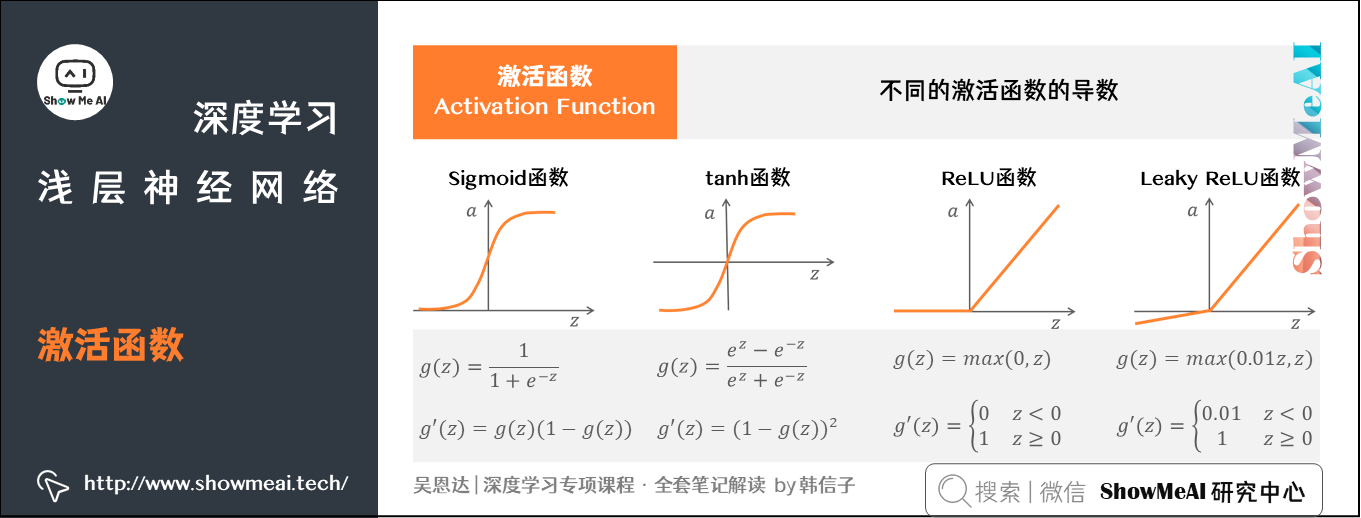
4.神经网络的梯度下降法

神经网络的梯度下降 Gradient Descent for Neural Networks

下面我们来一起看看，神经网络中的梯度计算。

我们依旧以浅层神经网络为例，它包含的参数为 $W^{[1]}$ ， $b^{[1]}$ ， $W^{[2]}$ ， $b^{[2]}$ 。

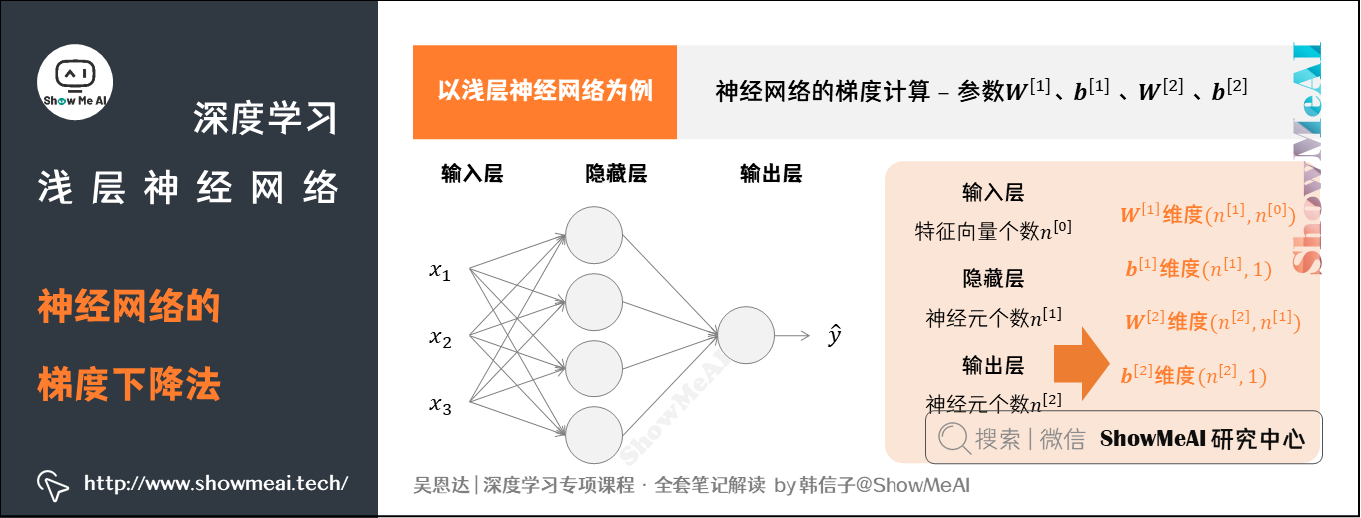
神经网络的梯度下降法

令输入层的特征向量个数 $n_x=n^{[0]}$ ，隐藏层神经元个数为 $n^{[1]}$ ，输出层神经元个数为 $n^{[2]}=1$ 。则：

$W^{[1]}$ 的维度为 $(n^{[1]},n^{[0]})$
$b^{[1]}$ 的维度为 $(n^{[1]},1)$
$W^{[2]}$ 的维度为 $(n^{[2]},n^{[1]})$
$b^{[2]}$ 的维度为 $(n^{[2]},1)$

4.1 神经网络中的梯度下降

上述神经网络的前向传播过程，对应的公式如下图左侧。反向传播过程，我们会进行梯度计算，我们先列出Cost Function对各个参数的梯度，如下图右侧公式。

神经网络的梯度下降法

其中，np.sum使用到python中的numpy工具库，想了解更多的同学可以查看ShowMeAI的 图解数据分析 系列中的numpy教程，也可以通过ShowMeAI制作的numpy速查手册 快速了解其使用方法)

4.2 反向传播（拓展补充）

直观理解反向传播 Backpropagation Intuition

我们使用上篇内容 神经网络基础 中的计算图方式来推导神经网络反向传播。回忆我们前面提到的逻辑回归，推导前向传播和反向传播的计算图如下图所示：

神经网络的梯度下降法

因为多了隐藏层，神经网络的计算图要比逻辑回归的复杂一些，如下图所示。

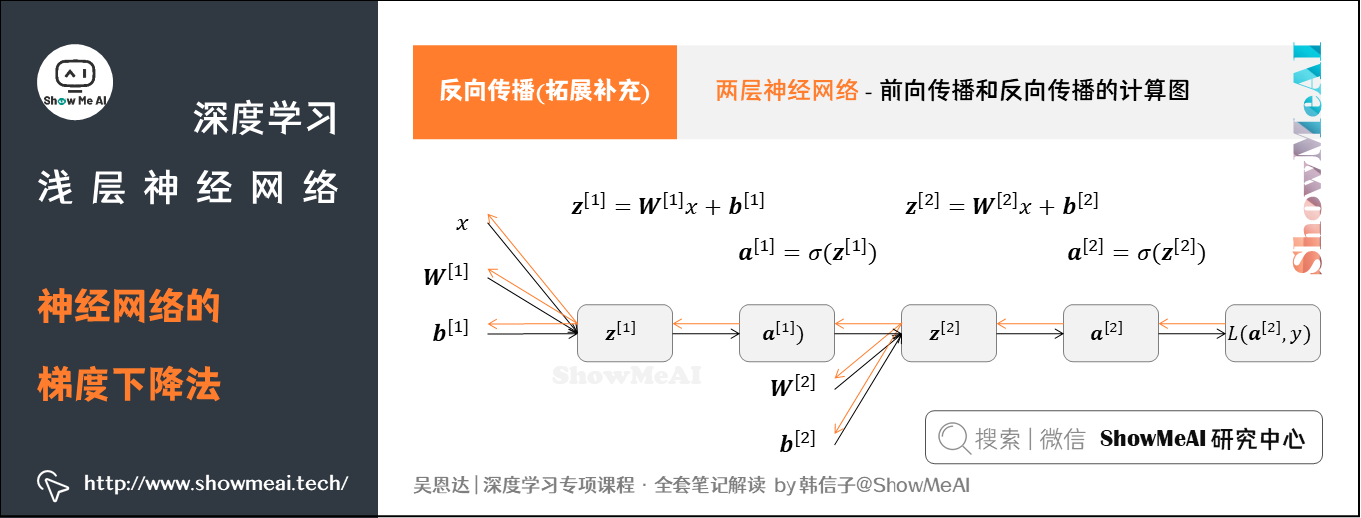
神经网络的梯度下降法

综上，对于浅层神经网络（包含一个隐藏层）而言，「单个样本」和「m个训练样本」的反向传播过程分别对应如下的6个表达式（都是向量化矩阵形式）：

神经网络的梯度下降法

5.随机初始化

随机初始化 Random + Initialization

5.1 全零初始化权重问题

我们在很多机器学习模型中，会初始化权重为0。但在神经网络模型中，参数权重 $W$ 是不能全部初始化为零的，它会带来对称性问题(symmetry breaking problem)，下面是分析过程。

假设一个浅层神经网络包含两个输入，隐藏层包含两个神经元。

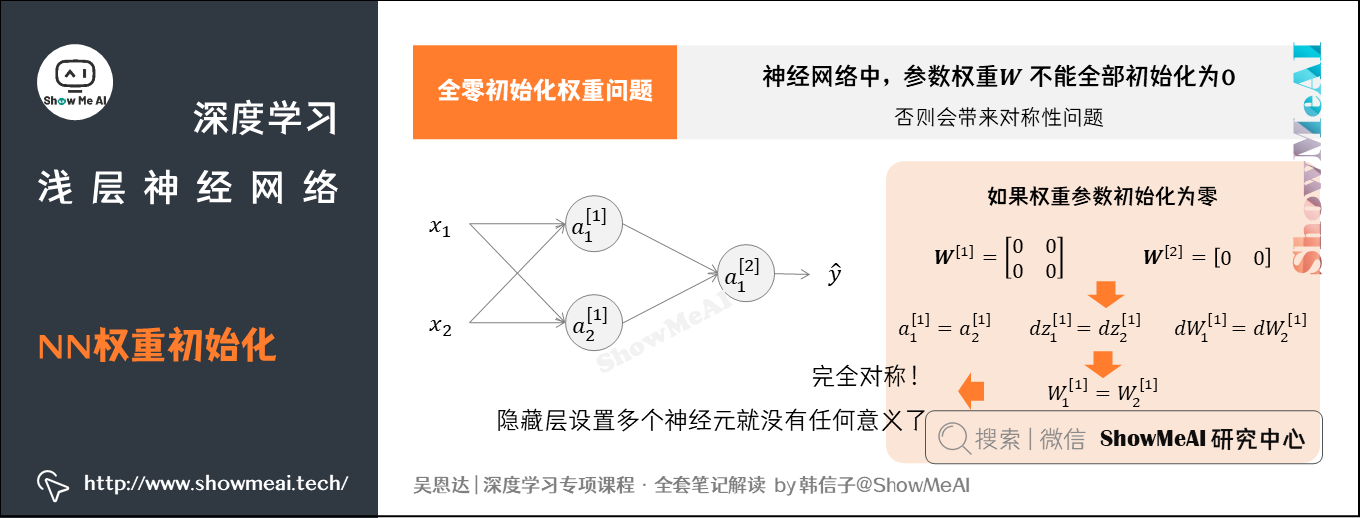
NN权重初始化

如果权重 $W^{[1]}$ 和 $W^{[2]}$ 都初始化为零，这样使得隐藏层第一个神经元的输出等于第二个神经元的输出，即 $a_1^{[1]}=a_2^{[1]}$ 。容易得到 $dz_1^{[1]}=dz_2^{[1]}$ ，以及 $dW_1^{[1]}=dW_2^{[1]}$ 。

我们发现：隐藏层两个神经元对应的权重行向量 $W_1^{[1]}$ 和 $W_2^{[1]}$ 每次迭代更新都会得到完全相同的结果， $W_1^{[1]}$ 始终等于 $W_2^{[1]}$ ，完全对称！这样隐藏层设置多个神经元就没有任何意义了。

当然，因为中间层每次只会有1个偏置项参数 $b$ ，它可以全部初始化为零，并不会影响神经网络训练效果。

5.2 解决方法

上述提到的权重W全部初始化为零带来的问题就是symmetry breaking problem(对称性)。解决方法也很简单：在初始化的时候， $W$ 参数要进行随机初始化，不可以设置为0。而 $b$ 因为不存在对称性的问题，可以设置为 0。

以 2 个输入，2 个隐藏神经元为例：

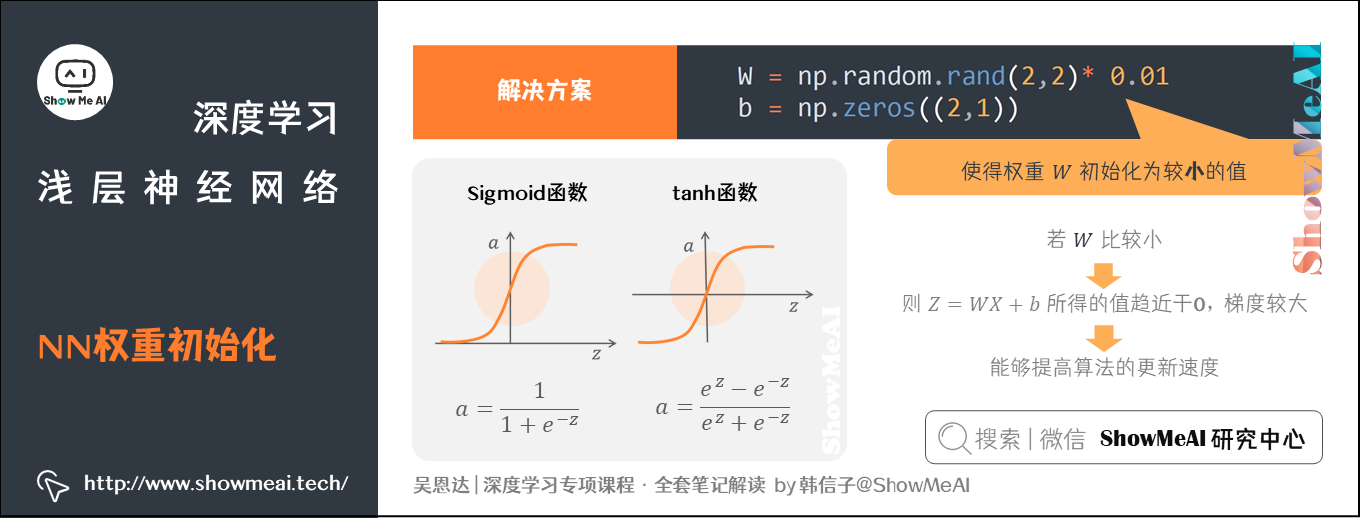
 W = np.random.rand(2,2)* 0.01
b = np.zeros((2,1))

这里将 $W$ 的值乘以 0.01(或者其他的常数值)的原因是为了使得权重 $W$ 初始化为较小的值，这是因为使用 Sigmoid 函数或者 tanh 函数作为激活函数时：

若 $W$ 比较小，则 $Z=WX+b$ 所得的值趋近于 0，梯度较大，能够提高算法的更新速度。
若 $W$ 设置的太大，得到的梯度较小，训练过程因此会变得很慢。

NN权重初始化

ReLU 和 Leaky ReLU 作为激活函数时不存在这种问题，因为在大于 0 的时候，梯度均为 1。如果输出层是Sigmoid函数，则对应的权重 $W$ 最好初始化到比较小的值。

ShowMeAI

『为AI硬核资料库(cool)而生！』构建AI解决方案，用知识加速每一次技术成长！公众号：ShowMeAI研究中心

深度学习教程 | 浅层神经网络

引言

1.神经网络表示

2.计算神经网络的输出

2.1 两层神经网络

2.2 单个样本计算方式

2.3 向量化计算

2.4 数据集向量化计算

3.激活函数

3.1 不同的激活函数与选择

(1) tanh 函数

(2) ReLU函数

(3) Leaky ReLU

3.2 使用非线性激活函数的原因

3.3 激活函数的导数

4.神经网络的梯度下降法

4.1 神经网络中的梯度下降

4.2 反向传播（拓展补充）

5.随机初始化

5.1 全零初始化权重问题

5.2 解决方法

参考资料

ShowMeAI系列教程推荐

推荐文章

公告

搜索

常用链接

我的标签

随笔分类

随笔档案

阅读排行榜

评论排行榜

推荐排行榜

最新评论